В представленной работе исследуется генерация второй гармоники твердотельного лазера с полупроводниковой накачкой.
Ключевые слова: твердотельный лазер, вторая гармоника, полупроводниковая накачка
Эффект генерации второй гармоники используется для расширения возможного длин волн лазерного излучения. Реализуется в основном в твердотельных лазерах. Также применяется для получения зондирующего излучения.
1. Нелинейная оптика.
Нелинейная оптика — это раздел физики, в котором изучаются процессы взаимодействия вещества со светом, результат которых зависит от интенсивности света. Одним из таких результатов является генерация гармоники лазерного излучения.
Это происходит из-за эффекта переизлучения. Когда на вещество попадает внешнее излучение в области взаимодействия будет происходить поляризация среды. Электрический дипольный момент, или степень поляризации, будет определяться значением напряженности электрического поля, а также диэлектрической восприимчивостью среды (1)
Р = Е(1)
где E — напряженность; — диэлектрическая восприимчивость среды. Для низких уровней напряженности (линейная оптика) f(E), но при увеличении интенсивности пучка напряженность будет возрастать до уровня, сравнимой с уровнем напряженности электрического поля атома, вследствие чего появляется зависимость свойств среды от Е. Диэлектрическая проницаемость среды ε определяется вектором поляризации P и связана с относительной диэлектрической восприимчивостью соотношениями (2) и (3)
![]() (2)
(2)
В общем случае диэлектрическая восприимчивость является функцией от напряженности. Тогда можно получить соотношение (4).
![]() (4)
(4)
Первое слагаемое определяет линейную поляризацию, а все остальные — нелинейную. Все коэффициенты χn не зависят от Е и характеризуют свойства вещества. В зависимости от их значений среды разделяют на квадратичные, кубические и т. д. При распространении в квадратичной среде вдоль оси z излучения основной гармоники c круговой частотой I = 2Iи скоростью vI степень поляризации определится как
P (t) = IE0 cos (Itz / vI) + IIЕ02 cos2 (Itz / vI) =
= IE0 cos (Itz / vI) + 0,5IIЕ02 1 + cos (2It2 z / vI).
Получается, что если воздействовать на квадратичную среду интенсивным, монохроматичным, обычным лазерным излучением, обладающим исходной частотой I, в ней может дополнительно появиться вторая гармоника излучения с частотой II, равной удвоенной I. Для осуществления подобного преобразования частоты необходимо, чтобы выполнялось условие волнового синхронизма: vI = vII или с / nI = с / nII, и, следовательно, nI = nII, где c скорость света в вакууме; nI, nII показатели преломления среды для первой и второй гармоник излучения. С квантовой точки зрения оно представляет собой закон сохранения импульса для фотонов, которые участвуют в этом процессе (6)
ħk(2ω)= ħk(ω)+ ħk(ω)=2 ħk(ω)(6)
Условие волнового синхронизма осуществимо в одноосных двулучепреломляющих кристаллах, в которых могут существовать «необыкновенный» и «обыкновенный» лучи. В таких кристаллах для необыкновенной волны показатель преломления зависит от направления распространения. Показатель преломления для такой волны имеет вид эллипсоида. Для обыкновенной волны показатель преломления не зависит от направления распространения. Угол между оптической осью нелинейного кристалла и волновыми векторами взаимодействующих волн называют углом волнового синхронизма.
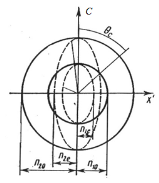
Рис. 1. С — оптическая ось. Сплошные кольца — сечения поверхностей показателей преломления обыкновенной волны; n10 — его значения для основной частоты, n20 — для второй гармоники. Пунктирные эллипсы — сечения поверхностей показателей преломления необыкновенной волны; n1e — его минимальное значения для основной частоты, n2e — для второй гармоники; ϴс — угол синхронизма
Важным является то, что сечение поверхности показателя преломления для необыкновенной волны на частоте 2ω пересекает сечение поверхности показатель преломления для обыкновенной волны на частоте ω.
- Генерация второй гармоники лазерного излучения.
Впервые генерация второй гармоники была продемонстрирована в 1961 г. группой американских ученых во главе с Франкеном. Его схема получения второй оптической гармоники является основной.
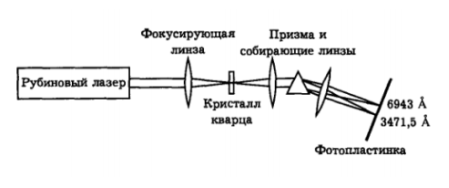
Рис. 2.
В этом опыте излучение, генерируемое рубиновым лазером, фокусировалось в кристалл кварца. Выходное излучение разворачивали в спектр при помощи дисперсионной призмы и фокусировали на фотопластинку. В результате можно было наблюдать, что помимо света на частоте лазера из кристалла выходил свет на удвоенной частоте. Это и была вторая гармоника. В опыте Франкена, излучение было очень слабым, но этот опыт дал значительный вклад в развитие нелинейной оптики. В дальнейшем было показано, что если использовать другие кристаллы, то можно добиться огромного увеличения эффективности генерации второй гармоники.
В нынешнее время существуют методы, с помощью которых можно преобразовать во вторую гармонику большую часть лазерного излучения. Генерация второй гармоники наблюдается в KTP (кристалл титанил фосфата калия), а также дигидрофосфате калия КН2РО4, и ниобате лития LiNbO3. В настоящее время в импульсных твердотельных лазерах за счет высокой плотности мощности достигнута генерация третьей и четвертой гармоник лазерного излучения.
- Результаты исследования.
В ходе исследования была получена временная характеристика, где Iλ2 — интенсивность второй гармоники, а Iλ3 — интенсивность накачки.
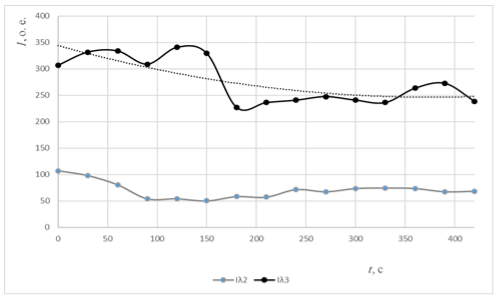
Рис. 3.
Из нее видно, что с течением времени интенсивность накачки уменьшается. Связано это, прежде всего, с нагревом лазера в процессе работы.
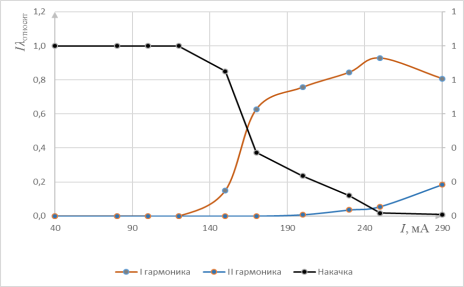
Рис. 4.
Также была получена характеристика относительных интенсивностей каждой составляющей излучения. Относительная интенсивность накачки уменьшается с появлением излучения лазера, а относительная интенсивность первой гармоники уменьшается, когда появляется вторая гармоника.
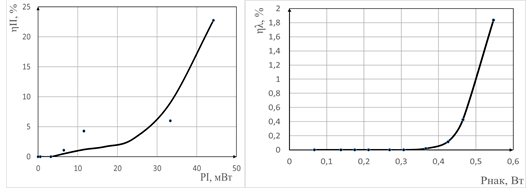
Рис. 5.
В результате были рассчитаны КПД преобразования первой гармоники во вторую и КПД генерации второй гармоники, которые составили 22,5 % и 1,9 % соответственно.
Заключение.
Данное исследование является актуальным на сегодняшний день, т. к. с помощью этого эффекта можно получать излучения с необходимыми длинами волн, для применения в различных отраслях.
Литература:
- Brunner W. Справочник по лазерной технике. М.: Энергоатомиздат, 1991. 544 с.
- Ландсберг Г. С. Оптика Учеб. пособие для вузов. М.: Физматлит, 2003. 848 с.
- Пихтин А. Н. Квантовая и оптическая электроника. Учебник. М.: Абрис, 2012. 573 с.
- Смирнов Е. А., Киселев А. С. Основы лазерной техники. Методическое пособие. СПб: Изд-во СПбГЭТУ «ЛЭТИ», 2015. 48 с.
- Научно-образовательный проект «Лазерный портал» [Электронный ресурс] — URL: http://www.laserportal.ru/ (дата обращения: 25. 05.2016).







