В данной работе рассматриваются основные моменты, связанные с управлением потоков движения заряженных частиц в ионно-плазменных технологических устройствах. Для увеличения эффективности нанесения материалов на заготовки различной формы и размеров необходимо решить задачу конфигурации магнитного поля. Проведен сравнительный анализ результатов решения с использованием программной среды Matlab и среды моделирования Comsol Multiphysics.
Ключевые слова: ионно-плазменные устройства, вакуумно-дуговой источник плазмы, магнетронные распылительные системы, магнитная система, катодное пятно, соленоид, движение заряженных частиц, магнитостатическая задача, Matlab, Comsol Multiphysics
Вакуумная техника и технология широко применяются для получения поверхностей различной структуры и состава, используемых как в промышленности, так и в экспериментальных исследованиях. Основными ионно-плазменными технологическими устройствами нанесения покрытия с помощью магнитных систем являются:
– магнетронные распылительные системы (аномально тлеющий разряд);
– вакуумно-дуговой источник плазмы коаксиальной конструкции (дуговой разряд).
Математическая постановка задачи заключается в решении самосогласованных нелинейных задач и сводится к расчетам полей, в которых осуществляется движение заряженных частиц и их траекторий. Выбор формы и величины индукции магнитного поля (МП) обусловлен конструкцией используемого вакуумно-дугового устройства, а также требованиями, предъявляемыми к наносимому покрытию и типу обрабатываемого изделия.
- Ионно-плазменные технологические устройства
Создание покрытий плазменными методами нашло широкое применение для решения специализированных технологических задач, из-за особых преимуществ перед другими существующими способами. Получают пленки полупроводников и полупроводниковых структур, различные пленки тугоплавких металлов, многокомпонентных сплавов
Постепенно снижая диапазон рабочих давлений, снижая показатель напряжения на разрядном промежутке распылительных систем, повышая скорость осаждения стремятся увеличить эффективность процесса распыления, уменьшая уровень загрязнений и радиационных дефектов уширяют области применения ионного распыления.
Основными конструкционными узлами ионно-плазменных устройств являются: система генерации и система управления электронным пучком.
Принцип действия магнетронных распылительный систем основан на аномально-тлеющем разряде, для которого характерно высокое значение управляющего напряжения по сравнению с током разряда. Особенностью данного устройства является более сложное строение магнитной системы, так как она выполняет несколько функций: 1) стабилизирует газовый разряд на поверхности мишени; 2) задает зону распыления материала катода; 3) управляет характером движения заряженных частиц. Таким образом система состоит из набора как соленоидов, так и постоянных магнитов.
Для решения технологической задачи за основу была взята модель вакуумно-дугового устройства коаксиальной конструкции (далее ВДУ), ввиду простоты реализации магнитного узла.
- Вакуумно-дуговой источник плазмы
ВДУ коаксиальной конструкции — это устройство катодного распыления материала под действием дугового разряда. Вакуумная дуга является частным случаем дуги низкого давления с холодным катодом и представляет сильноточный низковольтный разряд, реализуемый в глубоком вакууме и развивающийся в парах материала одного из электродов. При этом на катоде возникает яркое пятно, которое передвигается с большой скоростью (![]() ). Величина плотности тока достигает значений порядка
). Величина плотности тока достигает значений порядка ![]() (радиус которого
(радиус которого ![]() )
)
Принцип действия устройства основан на испарении материала катода под действием дуги низкого давления с автоэлектронной эмиссией. Дуговой разряд подразделяется на катодную и анодную дугу. Поверхностью анода является сам корпус установки.
Магнитная система включает в себя основные элементы стабилизирующий и фокусирующий соленоиды, однако в зависимости от технологической задачи их количество может быть намного больше двух. Первостепенными условиями работы устройства являются:
-
Величина магнитной индукции внешнего поля должна быть больше значения собственного (
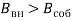 );
);
-
Плотность тока стабилизирующего соленоида должна быть выше плотности тока фокусирующего (
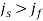 );
);
-
Температура катодной дуги должна быть выше температуры кипения материала катода (
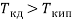 ).
).
-
Внутренняя площадь поверхности анода должна быть не менее
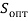 (значение
(значение 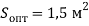 ).
).
Количество используемых катодных узлов зависит от требуемых условий итогового покрытия. Основными достоинствами устройства являются: простота исполнения, малый нагрев материала заготовки. Для напыления на заготовки протяженных размеров используют подвижную рамку.
- Взаимодействие заряженного пучка смагнитным полем.
Управляющие свойства магнитного поля в зоне транспортировки плазменного потока зависят, прежде всего, от геометрии силовых линий, в зависимости от параметров и структуры соленоидов. В процессе работы, генерируемый плазменный поток заполняет весь рабочий объем. При условии замагниченности электронов, когда параметр Холла, равный произведению циклотронной частоты на характерное время их столкновений значительно превышает единицу, движение отрицательно заряженной компоненты осуществляется вдоль силовых линий магнитного поля.
Величина влияния магнитного поля на заряженные частицы электроны и ионы сильно различна. Для их оценки вводят собственные показатели Холла: βe и βi. Их отношение пропорционально отношению масс электрона и иона. Соответственно, магнитное поле имеет большее влияние на электроны плазмы и раньше на них воздействует:
![]()
![]()
Траектория движения заряженных частиц имеет сложный трехмерный вид, при существовании магнитных и электрических полей. Однако, если относительное изменение этих полей в пределах ларморовского круга достаточно малы, то можно применять адиабатическое приближение. Тогда итоговую скорость частицы представляют в виде суммы скорости дрейфа ведущего центра и скорости вращения по ларморовской окружности вокруг него.
Если ![]() и
и ![]() (сила электрического поля) не равны нулю и не зависят от координат, то скорость движения частицы, ортогональной
(сила электрического поля) не равны нулю и не зависят от координат, то скорость движения частицы, ортогональной ![]() , представляют как:
, представляют как:
![]()
где ![]() — скорость ларморовского вращения;
— скорость ларморовского вращения; ![]() — скорость дрейфа, которая ортогональна действующей силе.
— скорость дрейфа, которая ортогональна действующей силе.
Если общие изменения в системе протекают медленно, а параметры характеризующие движения остаются постоянными, то его называют адиабатическим инвариантом. Места, где сгущаются линии магнитного поля, образуется магнитная пробка (или магнитное зеркало), от которой частица отражается.
- Расчет магнитных полей
Расчет магнитных полей представляет из себя сложную магнитостатическую задачу. Для ее решения использовались такие программные пакеты как Matlab и Comsol Multiphysics.
Методика расчета в среде Matlab основана на уравнениях Био-Савара, которые преобразованы с помощью системы цилиндрических координат для аксиально-симметричного поля. Для расчета разбивались на подобласти как области движения заряженных частиц под соленоидами, так и сама структура соленоида. Основные расчетные выражения для продольной и радиальной составляющей:
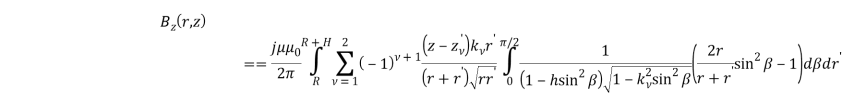
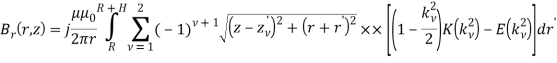
Решение задачи сводится к расчету уравнений по продольной переменной z.
Данные выражения включают в себя эллиптические интегралы первого, второго и третьего родов, а также сокращения:
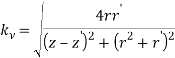
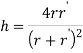
COMSOL Multiphysics — среда моделирования, предназначенная для моделирования и решения задач в различных областях физики. Данный программный пакет состоит из набора модулей (модуль плазмы, модуль постоянного и переменного тока), который облегчает процесс моделирования.
Методика расчета основана на решении уравнений Максвелла и методе конечных элементов (включает в себя системы дифференциальных уравнений для более точного воспроизведения физических процессов протекающих в данной технологической задаче.
Таблица 1
Список основных уравнений при решении задачи всреде ComsolMultiphysics
|
|
закона ампера |
|
|
уравнения Максвелла |
|
|
уравнение движения заряженной частицы в магнитном поле |
|
|
уравнение магнитной изоляции |
|
|
уравнение электрического и магнитных полей |
Итогом построения магнитостатической задачи являются графики поверхностей.
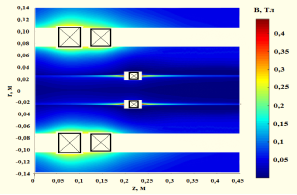
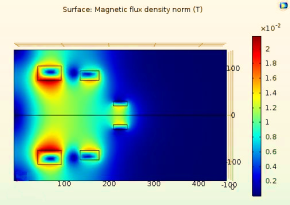
Рис. 1. Результаты работы программ Matlab и Comsol Multiphysics
Заключение
Результатом вычисления задачи магнитного поля с помощью программы Matlab основанный на методике, которая включает в себя уравнения Био-Савара показывает:
- Существует определенная погрешность вычисления магнитного поля вблизи соленоидов;
- Расчет проводится на определенном расстоянии от соленоидов и отсутствует возможность построения задачи с учетом их влияния на технологический процесс.
При построении задачи в программе Matlab расчет проводился с помощью заданных условий плотностей тока, габаритов соленоида и параметров токоведущего провода. Таким образом коэффициент заполнености меди составил порядка единицы, что повлияло также на результат расчета.
Итоги вычисления в среде моделирования Comsol Multiphysics в дальнейшем могут быть использованы при проектировании нестандартных задач, а также существует возможность ее расширения: учет геометрии провода, неидеальность толщины витка проводника соленоида, пронаблюдать характер движения заряженных частиц в поставленной задачи и прочие условия. Однако самый весомый недочет программы является — ее цена.
Выводы
Методика расчета в среде моделирования Comsol Multiphysics, основанная на решении уравнений Максвелла и методе конечных элементов позволяет более точно спрогнозировать процессы, проходящие в технологические задачи подобного рода и не только. Итоговый результат работы программы применим для дальнейших технических расчетов, так как программа полностью оптимизирована для решения технологических задач подобного характера. Проведенные исследования математического анализа распределения картины индукции магнитного поля позволяют в дальнейшем смоделировать характер движения заряженных частиц, и спрогнозировать параметры технологических процессов.
Литература:
- Сысоев Ю. А. Проблемы ионно-плазменных технологий на основе вакуумно-дугового разряда и пути их решения // Авиационно-космическая техника и технология, 2011, вып. (№) 7. С. 38–42.
- Ефремов А. Н., Светцов И. В., Рыбкин В. В. Вакуумно-плазменные процессы и технологии: учеб. пособие. Иваново.: Из-во ГОУВПО «ИГХТУ», 2006. 260 с.
- Лисенков А. А., Ветров Н. З. Вакуумные дуговые источники плазмы. СПб.: Энергоатомиздат, 2000.
- Вершин Н. Ф., Страумал Б. Б., Казакевич А. В. Коррозионная стойкость покрытий из оксида и нитрида титана на силикатном стекле, полученных методом вакуумно-дугового напыления // Электровакуумная техника и технология: тр. научн.-техн. сем., Москва, 1997/98 гг. / НИТУ «МИСиС», Москва, 1999, С. 43–46.
- Барченко В. Т., Гончаров В. Д., Лисенков А. А. Вакуумно-дуговой разряд на интегрально-холодном катоде // Плазменная эмиссионная электроника: тр. III международный Крейндлевский сем., Улан-Удэ, 23–20 июня 2009 г. / БНЦ СО РАН, 2009. С. 68–73
- Фурсей Г. Н. Автоэлектронная эмиссия // Соровский образовательный журнал, 2000, вып. (№) 11. С. 96–103.
- Данилин Б. С., Неволин В. К., Сырчин В. К. Исследование магнетронных систем ионного распыления материалов. — Электронная техника. Сер. Микроэлектроника, (69), с. 37–44.
- Пат. RU 2180472. Вакуумно-дуговой источник плазмы / Н. З. Ветров, В. Г. Кузнецов, А. А. Лисенков, Н. М. Радциг, И. В. Сабуров. Опубл. 10.03.2002, Бюл. № 3. c.
- Молоковский С. И., Сушков А. Д. Интенсивные электронные и ионные пучки. М.: Москва Энергоатомиздат, 1991. 303 с.
- Krzysztof M. K. Biblioteka problemów eksploatacji: działanie i budowa magnetronowych urządzeń rozpylających. М.: Radom, 1977. 177
- Плазменные ускорители / Под общей редакцией Л. А. Арцимовича. — М.: Машиностроение, 1973.
- Соленоид. Электромагнит // RZA. ORG. UA. Все о релейной защите. URL: http://rza.org.ua/elteh/read/59--Solenoid--Elektromagnit_59.html (дата обращения: 01.06.2016)..
- Половко А. М., Ганичев М. В. Mathcad для студента. М.: БХВ-Петербург, 2006. 336 с.
- Дьяконов В. П. Matlab: полный самоучитель. М.: ДМК Пресс, 2011. 768 с.
- Красников Г. Е., Нагорнов О. В., Старостин Н. В. Моделирование физических процессов с использованием пакета Comsol Multiphysics. М: НИЯУ МИФИ, 2012, 184 с.







