В данной статье рассматриваются моделирование индекса промышленного производства России на основе индексов промышленного производства составляющих отраслей. В качестве данных использованы ИПП различных отраслей с 2011 по 2015 год в помесячном виде. Данные взяты из открытых источников РосСтата.
Ключевые слова: промышленность, ИПП, регрессионные модели, эконометрика
В наши дни часто возникает необходимость в анализе и получении точного прогноза какого-либо экономического показателя домохозяйства, предприятия, государства или даже союза нескольких государств (Европейский Союз, Евразийский Союз). Чаще всего для этого обращаются к статистическим методам, в том числе и к методам эконометрики, с помощью которых можно изучить зависимость между различными экономическими показателями, а также исследовать временной ряд показателя, после чего на основе проведенного анализа сделать прогноз.
Промышленное производство — важнейшая составляющая мировой и российской экономик. В России, как и во всем мире, промышленное производство оценивается с помощью Индекса Промышленного Производства (ИПП). Очевидно, что положительная динамика ИПП говорит о хорошем экономическом положении в стране, а отрицательная о плохом. Отсюда возникает необходимость понимать, как поведет себя ИПП в краткосрочной или долгосрочной перспективе.
Рассмотрим понятие индекса производства. Это показатель, который характеризует совокупное изменение производства всех видов работ, товаров и услуг за сравниваемые периоды времени [2].
Индекс промышленного производства — это агрегированный индекс производства по таким видам деятельности как: «Добыча полезных ископаемых», «Обрабатывающие производства», «Производство и распределение электроэнергии, газа и воды» [2]. Расчетом и формированием индекса промышленного производства в России занимается Федеральная служба государственной статистики (Росстат).
Рассмотрим математическую формулу расчета индексов производства. Для начала изучим ее составляющие. Величина 
— это среднегодовая цена единицы товара в тысячах рублей в базисном году. Величины 
, 
, 
— производство в натуральном выражении в среднем за месяц базисного года, за t-период (период с начала года, отчетный месяц), t-1-период (соответствующие периоды предыдущего года, предыдущий месяц) соответственно. Также поясним понятие базисного года: это год, в котором структуры товарных цен, производства и добавочной стоимости относительно устойчивы.
Расчет индексов происходит в несколько шагов. На каждом рассчитывается три вида индексов:
1) Сначала рассчитывается индекс, который характеризует производственные
изменения в отчетный период t по сравнению со среднемесячным объемом базисного года — 
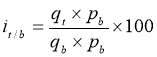
2) Далее считаем индекс, который характеризует изменение производства в прошедшем периоде t-1 по сравнению со среднемесячным объемом базисного года — 
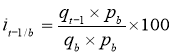
3) И, наконец, рассчитываем индексы 
, которые характеризуют изменение производства в периоде t в сравнении с t-1. Данные индексы получаем, проведя деление индексов, рассчитанных ранее
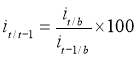
Согласно ОКВЭД (Общероссийский классификатор видов экономической деятельности) каждому виду экономической деятельности соответствует код. Так как индекс промышленного производства является агрегированным по видам деятельности таким, как C — «Добыча полезных ископаемых», D — «Обрабатывающие производства», E -«Производство и распределение электроэнергии, газа и воды», то для удобства можно использовать следующее обозначение: ИПП (C+D+E). А для краткого упоминания видов деятельности будем использовать эти самые коды, поэтому также введем в обращение: ИПП (С), ИПП (D), ИПП (E).
Стоит отметить, что у каждого подвида отрасли есть свой код согласно ОКВЭД. Например, химическое производство имеет код DG. Первая буква описывает вид экономической деятельности, к которой относится данное производство (обрабатывающие производства), а вторая буква уже является индивидуальной.
Самую большую долю в промышленности занимают «обрабатывающие производства». Разбирая структуру промышленности, выделим производства с самой большой долей: 24 % — это «добыча топливно-энергетических полезных ископаемых» (CA), 15 % — «производство кокса и нефтепродуктов» (DF), 12 % — «производство пищевых продуктов, включая напитки, и табака» (DA), 11 % — «металлургическое производство и производство готовых металлических изделий» (DJ).
Построим корреляционную матрицу между ИПП (С+D+E), ИПП (C), ИПП (D) и ИПП(E). Данные по индексам промышленного производства взяты из открытых источников Росстата и представляют собой помесячные показатели с 2011 по 2015 год, в каждой выборке присутствует по 60 элементов, которые выражены в процентах (период с начала отчетного года к соответствующему периоду предыдущего года).
Таблица 1
|
ИПП |
C+D+E |
DA |
DF |
DJ |
|
C+D+E |
1 |
|||
|
DA |
0,87 |
1 |
||
|
DF |
0,99 |
0,83 |
1 |
|
|
DJ |
0,17 |
0,28 |
0,05 |
1 |
Из таблицы 1 видно, что самый высокий коэффициент корреляции наблюдается между ИПП(C+D+E) и ИПП(D). Это может говорить о том, что отечественная промышленность в целом подвержена влиянию тех же факторов, которые влияют на отрасль «обрабатывающих производств». И так как доля D в структуре промышленности самая высокая, с большой вероятностью любые колебания ИПП (D) отразятся на ИПП (C+D+E).
Теперь построим корелляционную матрицу между ИПП (C+D+E), ИПП (DA), ИПП (DF) и ИПП (DJ). Отрасль СА рассматривать не будем по причине того, что она составляет 89 % добывающих производств (C). Вместо нее рассматривается целиком все С.
Из второй таблицы видно, что имеется высокая зависимость между показатаелями всей промышленности и показателями металургического производства(DJ).
Таблица 2
|
ИПП |
C+D+E |
DA |
DF |
DJ |
|
C+D+E |
1 |
|||
|
DA |
0,59 |
1 |
||
|
DF |
0,59 |
0,29 |
1 |
|
|
DJ |
0,95 |
0,47 |
0,48 |
1 |
Теперь построим две линейные регрессионые модели и попытаемся понять, можно ли сделать прогноз ИПП в целом, в зависимости от данных ИПП (D) и ИПП (DJ). Построим первую парную регрессию. В качестве зависимой переменной 
возьмем ИПП (С+D+E), а в качестве объясняющей 
— ИПП (D). Таким образом получим вид регресии 
, где 
— остатки регрессии, 
— значения регрессионной модели. Сама модель имеет вид: 
. Найдем коээфициенты модели с помощью «метода наименьших квардратов».
В каждой выборке будем строить модели по 56 элементам. Приведем расчитанные показатели критериев качества для модели 
:
|
|
|
|
|
|
|
|
Гомоскед. |
|
0,97 |
0,30 |
0,42 |
45,53 |
33,23 |
45,12 |
2035 |
да |
Для того чтобы интерпретировать модель, воспользуемся коэффициентом эластичности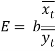 
. Oн демонстрирует на сколько процентов меняется в среднем когда увеличится на 1 % от 
.
В нашем случаем E = 0,54, это значит чуть меньше 1 %.
Вернемся к показателям качества, приведем табличные значениях различных критериев при 
= 2и 
= 4,02. Сделаем вывод: все показатели демонстрируют хорошее качество модели, она может быть использована для построения прогноза.
Далее построим вторую парную регрессию. В качестве зависимой переменной возьмем ИПП (С+D+E), а в качестве объясняющей — ИПП (DJ). Модель также будет иметь вид: . Коэффициенты также найдем при помощи метода наименьших квадратов.
Получили модель: 
. Приведем показатели качества модели.
|
|
|
|
|
|
|
|
Гомоскед. |
|
0,89 |
0,66 |
0,88 |
20,92 |
19,98 |
20,73 |
429,81 |
Да |
Все показатели говорят о хорошем качестве модели. Высокий коэффициент детерминации, низкие 
и 
, все t-рассчетные и F-рассчетная выше табличных значений, модель гомостедастична.
Подведем итоги. Давать прогноз поведения динамики ИПП (C+D+E) можно основываясь и на ИПП отдельных подвидов промышленности, например, металлургии, так как динамики некоторых отраслей ведут себя в целом как динамика всего отечественного промышленного производства.
Литература:
- Дуброва Т. А. Статистические методы прогнозирования в экономике. М.: Московский международный институт эконометрики, информатики, финансов и права, 2003. 50 с.
- Официальная статистическая методология исчисления индекса промышленного производства. Приказ Росстата от 08.05.2014 № 301http://www.gks.ru/free_doc/new_site/metod/prom/ofic_met.doc
