Современная экономическая наука имеет в своем арсенале большое количество разнообразных приёмов и методов прогнозирования финансовых показателей, в том числе в плане оценки возможного банкротства.
В зарубежной экономической литературе широко распространены модели Р. Лиса, Д. Фулмера, Г. Спрингейта, Р. Таффлера, Э. Альтмана, однако, как отмечают многие российские авторы, многочисленные попытки применения иностранных моделей прогнозирования банкротства в отечественных условиях не принесли достаточно точных результатов. Среди отечественных методик прогнозирования вероятности банкротства можно отметить модели Л. В. Донцовой, Е. С. Стояновой, Р. С. Сайфулина и Г. Г. Кадыкова, О. П. Зайцевой, В. В. Ковалева, Г. В. Савицкой. Несмотря на наличие большого количества моделей, методик, позволяющих спрогнозировать наступление банкротства фирмы с той или иной степенью вероятности, в этой области существует множество проблем. Известные отечественные модели, имеют ряд своих недостатков, достаточно часто результаты, полученные с помощью этих моделей, расходятся с реальными значениями.
В связи с этим исследуются новые пути решения поставленной задачи, например применение новых методов основанных на моделировании. Одним из таких методов является применение аппарата искусственных нейронных сетей.
По сравнению с традиционными технологиями нейронные сети обладают следующими достоинствами [2, 3]:
- Универсальность. Нейронные сети не зависят от свойств входных данных, для них не существует требования к определенному типу распределения исходных данных, либо требования к линейности целевых функций.
- Простота. Использование нейронных сети не требует специальной подготовки, для практического применения нет необходимости глубоко вникать во внутренние механизмы работы сети, в отличие от статистических методов, требующих фундаментальных знаний из области теории вероятностей и математической статистики.
- Не существует проблемы «проклятия размерности». Они способны моделировать зависимости в случае большого числа переменных.
- Ускоряют процесс нахождения зависимости за счет одновременной обработки данных всеми нейронами.
Основной задачей исследования являлась реализация одного из видов искусственных нейронных сетей для решения экономических задач, а именно — прогнозирования банкротства авиакомпаний.
Для построения нейронной сети была разработана топология, определен механизм обучения и тестирования. В процессе исследования была создана выборка входных данных, построен алгоритм. Для реализации алгоритма использовался математический пакет MatLab. (Таблица 1).
Таблица 1
Алгоритм реализации нейронной сети
|
1 |
Подготовка входных данных |
|
2 |
Определение архитектуры сети |
|
3 |
Обучение нейронной сети |
|
4 |
Проверка корректности работы ИНС |
Было принято решение остановиться на модели многослойного персептрона и алгоритме обратного распространения.
Отличительными признаками многослойного персептрона являются:
- Каждый нейрон сети имеет нелинейную функцию активации.
- Помимо входного и выходного слоя, он имеет ещё несколько слоев, называемых скрытыми.
- Многослойный персептрон отличается высокой степенью связанности (по принципу «каждый с каждым»).
В работе использован самый известный вариант алгоритма обучения нейронной сети — алгоритм обратного распространения [2]. С помощью алгоритма обратного распространения вычисляется вектор градиента поверхности ошибок. Этот вектор указывает направление кратчайшего спуска по поверхности из данной точки, поэтому если мы «немного» продвинемся по нему, ошибка уменьшится. Последовательность таких шагов (замедляющаяся по мере приближения к дну), в конце концов, приведет к минимуму того или иного типа. Определенную трудность здесь представляет вопрос о том, какую нужно брать длину шагов.
При большой длине шага сходимость будет более быстрой, но имеется опасность «перепрыгнуть» через решение или уйти в неправильном направлении. Напротив, при маленьком шаге, вероятно, будет схвачено верное направление, однако при этом потребуется очень много итераций. На практике величина шага берется пропорциональной крутизне склона (так что алгоритм замедляет ход вблизи минимума) с некоторой константой, которая называется скоростью обучения.
В качестве данных для рассматриваемой задачи оценки вероятности банкротства, которые будут подаваться на входной слой нейронов, были выбраны коэффициенты, присутствующие в пятифакторной модели Альтмана, а также следующие коэффициенты:
- Коэффициент текущей ликвидности.
- Коэффициент обеспеченности собственными средствами.
- А также коэффициенты из пятифакторной модели Альтмана.
Таблица 2
Входные параметры
|
Коэффициент текущий ликвидности |
= оборотные активы/краткосрочные обязательства |
|
Коэффициент обеспеченности собственными средствами |
= (собственный капитал — внеоборотные активы) / оборотные активы |
|
Коэффициенты пятифакторной модели Альтмана |
|
|
K1 |
= оборотный капитал/ сумму активов |
|
K2 |
= не распределенная прибыль/сумма активов |
|
K3 |
= операционная прибыль/сумма активов |
|
K4 |
= рыночная стоимость акций/ заемные пассивы |
|
K5 |
= выручка/ сумма активов |
В рассматриваемой задаче прогнозирования банкротства наряду с выбором модели и конфигурации важным моментом является сбор статистики по предприятиям. Необходимо понимать для предприятий, какого сектора строится нейронная сеть. Точность прогноза возрастает при обучении нейронной сети на выборке из предприятий одной отрасли и значительно уменьшается при обобщенной выборке.
Данная конфигурация нейронной сети разрабатывалась для авиакомпаний. В качестве исходных данных бралась финансовая отчетность 16 компаний, 8 из которых являются — банкротами, а остальные 8 — действующими (в качестве источника данных использовалась база данных на сайте Интерфакса). Необходимые данные были взяты из Бухгалтерского баланса организации (Форма 1) и из Отчета о финансовых результатах (Форма 2).
Все компании были разбиты на 2 одинаковых множества по 16 компаний — обучающее множество и тестирующее множество. Деятельность организаций рассматривалась в период с 2013 по 2014 год (рис. 1, рис. 2).
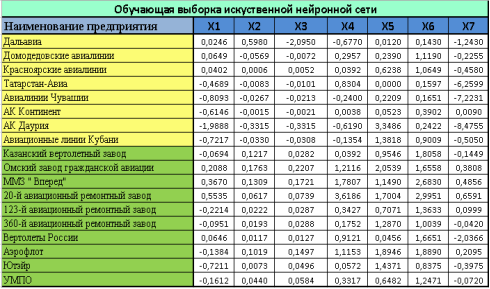
Рис. 1.Обучающая выборка
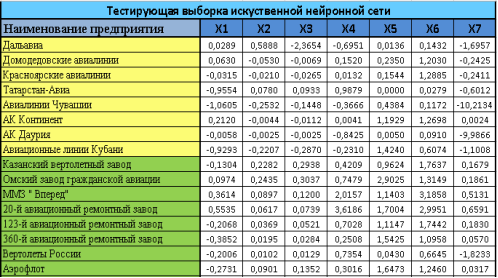
Рис. 2.Тестируемая выборка
Для выходных значений был задан диапазон от 0 до 1. Если выходное значение приближается к 0, то предприятие признается банкротом; если выходное значение приближается к 1, то положение предприятия оценивается как стабильное.
Порядок подачи на входной слой нейронной сети был определён практическим путем, был выбран тот вариант, при котором реальные значения совпали с результатами на выходе нейронной сети.
Отметим, что для реализации процесса обучения нейронной сети необходимо использовать в качестве передаточных непрерывные функции, имеющие непрерывную производную. Поскольку диапазон выходов должен быть от 0 до 1, то разумно выбрать в качестве выходной сигмоидальную функцию активации (рис. 3).
![]() (1)
(1)
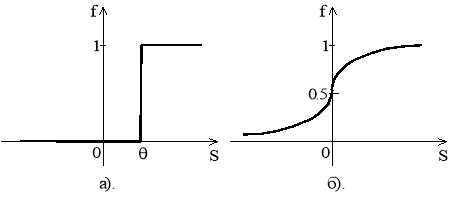
Рис. 3.Виды функций активации
Следует отметить, что сигмоидальная функция дифференцируема на всей оси абсцисс. Кроме того она обладает свойством усиливать слабые сигналы лучше, чем большие, и предотвращает насыщение от больших сигналов, так как они соответствуют областям аргументов, где сигмоида имеет пологий наклон.
Поскольку нейронные сети могут быть склонны к такому явлению как переобучение, необходимо контролировать число итераций или минимальное значение градиента ошибок, подбирая их таким образом, чтобы ошибка на тестовом наборе данных была наименьшей из возможных. Исследование данной задачи показало, что следует использовать значение градиента около 0,01. Кроме того количество нейронов в скрытом слое не должно превышать число нейронов во входном слое. В данной работе в скрытом слое 6 нейронов (рис. 4)
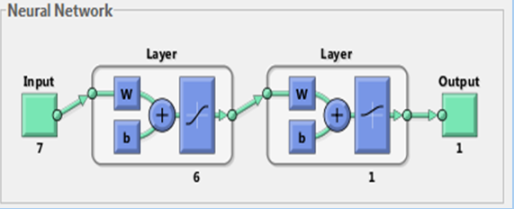
Рис. 4.Структура нейронной сети
Значение средней квадратичной ошибки также определяет качество обучения нейронной сети, представляется данный параметр в виде графика (рис. 5).
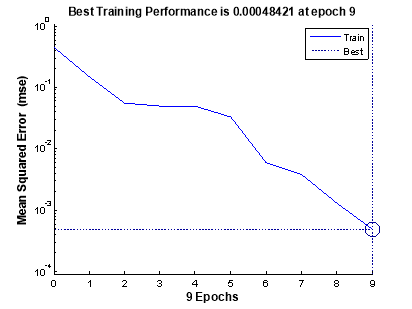
Рис. 5.Значение средней квадратичной ошибки
По результатам регрессионного анализа реального и смоделированного выхода для обучающей выборки, можно судить о коэффициенте корреляции. Поскольку коэффициент близок к единице, то сеть уверенно классифицирует все предприятия из обучающей выборки.
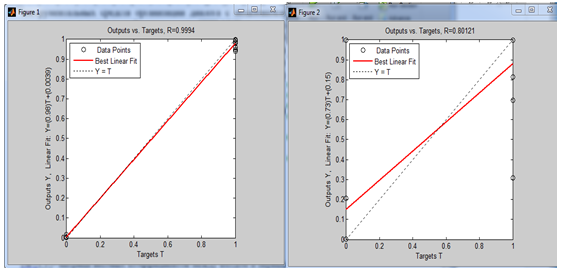
Рис. 6.Значение коэффициента корреляции
Коэффициент корреляции равен 0,8, что говорит о высоком качестве полученной нейронной сети.
Определим конечную архитектуру построенной нейронной сети. Это будет двухслойная сеть с прямой передачей и обратным распространением ошибки с функцией активацией гиперболический тангенс для скрытого слоя нейронов и сигмоидальной передаточной функцией на выходе. Т. к. второй слой является выходным, а на выходе мы имеем один параметр, то второй слой будет состоять только из одного нейрона.
Таблица 3
Итоговая таблица
|
Вид нейронной сети |
Многослойный персептрон |
|
Количество нейронов на входном слое |
7 |
|
Количество скрытых слоев |
2 |
|
Количество нейронов на скрытом слое |
6 |
|
Количество нейронов на выходном слое |
1 |
|
Характер обучения |
Обучение с учителем |
|
Алгоритм обучения |
Алгоритм обратного распространения ошибки |
|
Функция активации |
Гиперболический тангенс |
Последним этапом исследования будет проверка корректности работы нейронной сети. Для этого подаём на входной слой всю тестовую выборку по 16 компаниям и сверяем результат на выходном слое нейронной сети с реальным положением компании (рис. 7).
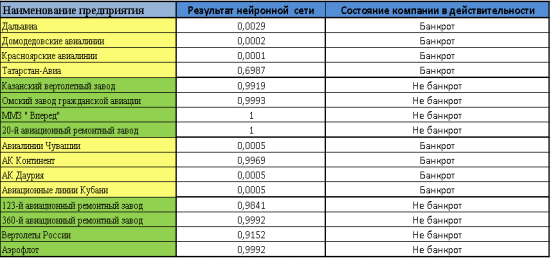
Рис. 7.Результаты
Во всех случаях нейронная сеть выдала правильный результат, а следовательно, успешно прошла проверку.
Проведенное исследование прогноза банкротства предприятия может быть использовано:
- инвестиционными компаниями при выборе предприятия для вложения инвестиций
- для статистических исследований
- для компаний планирующих сотрудничество с незнакомым предприятием.
Литература:
- Журов В. А. Процесс разработки моделей для прогнозирования банкротства предприятий // Финансовый менеджмент. — 2007. — № 1 — С. 53–66.
- ОРЛОВ А. И. Менеджмент. М.: Изумруд, 2003. — 298 с.
- HAYKIN S. Neural Networks: A Comprehensive Foundation. MacMillan College Publishing Co., New York, 1994.
- http://www.interfax.ru
- http://www.prime-tass.ru







