Критерии эредитарности экономического процесса и эффект памяти

В статье предлагаются критерии, позволяющие выявлять такие экономические процессы, в которых необходимо учитывать эффекты памяти. Если эти критерии выполняются, то следует использовать такие модели поведения, в которых экономические агенты и субъекты наделены памятью о предыдущих изменениях экономического процесса.

Эредитарность экономического процесса — это свойство зависимости процесса от экономических агентов и субъектов, обладающих памятью о прошлом данного процесса. При описании эредитарного процесса необходимо учитывать не только текущее состояние и бесконечно близкие к нему предыдущее состояния, но и все предыдущие состояния данного процесса. Математически это означает, что для описания такого процесса недостаточно знания начальных значений параметров состояния и конечного числа производных целого порядка по времени для этих параметров. Другими словами, эредитарный процесс зависит от предыдущей истории изменения процесса, и поэтому можно сказать, что этот процесс с памятью. Одним из первых, кто сформулировал базовые принципы эредитарности был итальянский математик Вито Вольтерра. В своих работах он использовал интегральные уравнения целого порядка для описания эредитарных процессов [1, c. 226–229]. Кроме того, помимо производных целых порядков, известны производные нецелых (дробных) порядков [2, 3, 4]. В настоящее время используются различные виды производных нецелого порядка, предложенные Риманом, Лиувиллем, Летниковым, Сониным, Вейлем, Риссом, Капуто [2]. Более того, известно, что производные и интегралы нецелых порядков позволяют описывать эредитарные процессы с памятью [4]. В последнее время производные нецелого порядка стали пременяться к описанию экономических процессов (смотрите статьи [5, 6] ссылки в них).

Можно в качестве критерия эредитарности экономического процесса предлагать следующее утверждение: если экономический процесс описывается используя интегральные уравнения, типа уравнения Волтерра, или производные нецелого порядка, то такой процесс является эредитарным. Однако такой подход не очень конструктивен на практике, когда исходной информацией является некоторая зависимость экономического показателя Y от фактора X. В связи с этим важно иметь некоторые критерии, позволяющие предположить эредитатарность в изучаемом экономическом процессе. И если условия этого критерия выполняются, то можно применять математический аппарат интегральных уравнений и производных нецелого порядка для построения моделей исследуемого экономического процесса.

Рассмотрим экономический процесс, в котором показатель (индикатор) Y зависит от некоторого фактора X. Например, Y — описывает спрос на товар, а X — цену этого товара. В общем случае, зависимость Y от X не является однозначной [7]. Однозначной будет только зависимость Y и X от времени. В общем случае экономический показатель (индикатор) Y и связанный с ним фактор X зависят от времени t. Используя метод наименьших квадратов для интерполяции непрерывными функциями (например, полиномами), можно получить однозначные дифференцируемые функции X=X(t) и Y= Y(t). В общем случае, нельзя исключить время, и представить зависимость Y от X в виде однозначной дифференцируемой функции вида Y=Y(X). Неоднозначность зависимости Y от X может быть обусловлена влиянием эффектов памяти на данный экономический процесс. Неоднозначность может быть обусловлена тем, что поведение экономических агентов и субъекты определяется их знанием (памятью) предыдущих состояний и изменений экономического процесса.

Очевидно, что если для некоторого конечного интервала времени существует постоянная b, такая что X(t-b)=X(t) для всех t из этого интервала, и кроме этого, выполняется равенство Y(t-b)=Y(t) для всех t из этого же интервала, то можно утверждать, что эффектами памяти можно пренебречь. Другими словами, предположим, что существует два одинаковых участка графика X(t), которые совпадут при сдвиге на некоторое значение b вдоль оси t, и аналогичное совпадение будет существовать и для участков графика Y=Y(t). Очевидно, что в данном случае, при тех же значениях X мы получаем совпадающие значения Y. В результате в тех же условиях субъект экономической деятельности вел себя так же, как и раньше. В этом случае можно пренебречь, что субъект обладает памятью. Однако такая ситуация реализуется далеко не всегда.

Для иллюстрации эффекта памяти рассмотрим некоторую упрощенную модельную ситуацию, близкую к реальным экономическим процессам, проходившим недавно. Предположим, что в течение нескольких месяцев курс национальной валюты резко падал по отношению к иностранной валюте. Большинство субъектов, чтобы сохранить свои сбережения, обменяли имеющуюся у них национальную валюту на иностранную. После этого, период резкого ослабления национальной валюты сменился несколькими месяцами её укрепления. Через полгода, период резкого ослабления национальной валюты повторился. Можно предполагать, что значительная часть субъектов, как минимум, не будет спешить обменять имеющеюся у них национальную валюту на иностранную. Поведение субъектов изменится. Многие из них будут учитывать, что год назад период резкого ослабления сменился периодом укрепления национальной валюты. Другими словами, экономические субъекты помнят изменения спроса и обменного курса иностранной валюты, которые были ранее. Аналогичная ситуация могла происходить с разными видами товаров (например, гречка, сахар, электронная техника и др.).

Отметим, что экономический анализ описанной упрощенной модельной ситуации был проделан в работах [7, 8]. В статье [7] была проанализирована зависимость объемов Q биржевых торгов по доллару США по отношению к средневзвешенному курсу P доллара США к рублю на торгах ЕТС в период с января по декабрь 2015 года. Были показаны ограничения на применимость понятия точечной эластичности, обусловленные неоднозначностью функций Q=Q(P). В работе [8] была исследована эластичность внебиржевого кассового оборота (спот) валютного рынка РФ в зависимости от средневзвешенного курса рубля к доллару США. В качестве объектов сравнения рассматривались два пятимесячных периода с августа по декабрь в 2014 и 2015 годах. В работах [5, 6, 7, 8] были предложены обобщения понятия точечной эластичности, позволяющее учесть наличие у покупателей памяти об изменения цены и спроса.

При этом в работах [7, 8] не были предложены явные критерии, позволяющие определять наличие или отсутствие эффекта памяти в экономическом процессе, и не сформулированы необходимые условия эредитарности экономического процесса. В статьях подчеркивалось, что эффект памяти связан с неоднозначностью зависимости показателей (индикатора) от экономических факторов. Однако для исследования экономических процессов важно иметь более точный критерий возможности пренебрегать или учитывать наличие памяти у экономических субъектов в экономических процессах.

Прежде чем предложить критерии эредитарности экономического процесса, сначала сформулируем необходимое условие возможности пренебрегать эффектами памяти в экономическом процессе, описываемом изменениями показателя (индикатор) Y(t) зависящего от некоторого фактора X(t): Пусть существуют такие константы a и b, что X(a(t-b))=X(t) для всех t из некоторого интервала, и существует такая постоянная c, что Y(a(t-b))=Y(t)+c для всех t из этого же интервала. Тогда можно говорить, что экономический процесс не является эредитарным и эффектом памяти можно пренебречь. Очевидно, что предлагаемые равенства, не позволяют утверждать, что их нарушение означает необходимость учета эффектов памяти. Как минимум равенство можно ослабить, требуя совпадения с точностью, используемой в интерполяции Y и X полиномами.

Сформулируем теперь необходимые условия, позволяющие утверждать о необходимости учета эффектов памяти в экономическом процессе, описываемом функциями X=X(t) и Y= Y(t). В алгебраическом критерии, используются относительные изменения показателя Y(t) и фактора X(t).

выполняется для всех моментов времени t из некоторого конечного интервала , и при этом не существует такой постоянной c, чтобы неравенство

выполнялось на интервале . Тогда можно говорить, что экономический процесс является эредитарным и эффектом памяти пренебречь нельзя.

В качестве другого подхода к проверке существования эффектов памяти в экономическом процессе можно использовать интегральные преобразования [9]. Поскольку показатель и фактор рассматриваются как функции времени, то удобно использовать преобразование Лапласа [9 c.30–75]. Преобразование Лапласа активно применяется для исследования свойства динамических процессов и для решения линейных дифференциальных и интегральных уравнений. Обозначим преобразование Лапласа функции X(t) через L{X(t)}(s), которое определяется формулой

Аналогично преобразование Лапласа функции Y(t) будем обозначать через L{Y(t)}(s). Учитывая, что преобразование Лапласа производной записывается в виде

,

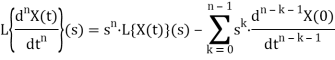можно сформулировать следующий критерий эредитарности экономического процесса.

Интегральное условие эредитарности. Пусть функция Y(t) показывает изменение некоторого индикатора в экономическом процессе в зависимости от изменения фактора X(t) при неизменности других факторов. Пусть существуют такие константы , и , (k=0,1,…,m; j=0,1,…,n), что выполняется равенство

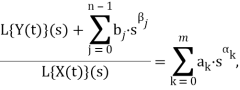
где и хотя бы одна из постоянных (k=0,1,…,m) является нецелой. Тогда можно говорить, что экономический процесс является эредитарным, а память носит степенной характер.

Предлагаемый алгебраический критерий эредитарности экономического процесса является только необходимым, но не достаточным условием. При этом сформулированный критерий является достаточным условием эредитарности степенного типа. Следует отметить, что при выполнении интегрального условия эредитарности показатель Y(t) может быть получен из фактора X(t) действием линейного дифференциального оператора нецелого порядка, в котором присутствует как минимум одна производная нецелого порядка. Это утверждение вытекает из свойств производных нецелого порядка [10, c.103–109]. В этом случае исследование эредитарных процессов может вестись в рамках моделей дробной динамики, активно развиваемой в естественных науках [4, 11, 12]. Отметим, что методы дробной динамики, используемые в естественных науках, в последнее время стали применяться для построения различных экономических моделей [13, 14, 15, 16, 17].

В заключении, можно сказать, что стандартное описание экономических процессов, которое не учитывает эффекты памяти, справедливо лишь для достаточно медленно меняющихся экономических агентов и субъектов. Для экономических субъектов меняющихся быстро по сравнению с характерными временами изменений в экономическом процессе, ситуация усложняется. В этом случае, поведение экономических субъектов может зависеть не только от экономического процесса в данный момент времени t, но и от его состояний в предыдущие моменты времени. В результате в экономическом анализе следует использовать модели поведения субъектов с памятью.

Литература:

1. Вольтерра, В. Теория функционалов и интегральных и интегро-дифференциальных уравнений. — Пер с англ. — М.: Наука, 1982. — 304 с.
2. Kilbas, A.A.; Srivastava, H.M.; Trujillo, J. J. Theory and Applications of Fractional Differential. Equations. — Amsterdam: Elsevier, 2006. — 540 с.
3. Учайкин, В. В. Метод дробных производных. — Ульяновск: Артишок, 2008. — 512 с. ISBN 978–5-904198–01–5
4. Tarasov, V. E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media. — New York: Springer, 2011. — 505 с.
5. Tarasova, V.V.; Tarasov, V. E. Elasticity for economic processes with memory: Fractional differential calculus approach // Fractional Differential Calculus. — 2016. — Vol. 6. — № 2. — P. 219–232.
6. Тарасова, В.В.; Тарасов, В. Е. Ценовая эластичность спроса с памятью // Экономика, cоциология и право. — 2016. — № 4–1. — С. 98–106.
7. Тарасова, В.В.; Тарасов, В. Е. О применимости точечной эластичности спроса по цене для биржевых торгов по доллару США // Научная перспектива. — 2016. — № 6 — С. 6–11.
8. Тарасова, В.В.; Тарасов, В. Е. Эластичность внебиржевого кассового оборота валютного рынка РФ // Актуальные проблемы гуманитарных и естественных наук. — 2016. — № 07 (90). — Статья принята в печать.
9. Диткин, В.А.; Прудников, А. П. Интегральные преобразования и операционное исчисление. — Москва: Физмагиз, 1961. — 524 с.
10. Podlubny, I. Fractional Differential Equations. — San Diego: Academic Press, 1998. — 340 p.
11. Klafter, J.; Lim, S.C.; Metzler, R. (Editors), Fractional Dynamics. RecentAdvances.Singapore: WorldScientific, 2011. — 515 p.
12. Тарасов, В. Е. Модели теоретической физики с интегро-дифференцированием дробного порядка. Москва: ИИКИ, 2011. — 568 с. ISBN 978–5-4344–0013–8
13. Scalas, E.; Gorenflo, R.; Mainardi, F. Fractional calculus and continuous-time finance. // Physica A. — 2000. — Vol.284. — № 1–4. — P.376–384.
14. Laskin, N. Fractional market dynamics. // Physica A. — 2000. — Vol.287. — № 3. — P.482–492.
15. Mainardi, F.; Raberto, M.; Gorenflo, R.; Scalas, E. Fractional calculus and continuous-time finance II: The waiting-time distribution. // Physica A. — 2000. — Vol.287. — № 3–4. — P.468–481.
16. Skovranek, T.; Podlubny, I.; Petras, I. Modeling of the national economies in state-space: A fractional calculus approach. // Economic Modelling. — 2012. — Vol.29. — № 4. — P. 1322–1327.
17. Tenreiro Machado, J.A.; Mata, M. E. A fractional perspective to the bond graph modelling of world economies. // Nonlinear Dynamics. — 2015. — Vol.80. — № 4. — P. 1839–1852.