В современную эпоху необходимо искать другие модели преподавания предмета в отличие от традиционных. Вопросы гуманизации и демократического педагогического процесса стали центральными. Каждый педагог ищет эффективные способы воздействия на учащихся, которые дают возможность ученику двигаться вперед в развитии ума, воли и чувств.
Одной из наиболее эффективных форм работы с детьми, способствующих их движению вперед в развитии ума, воли и чувств, является правильно организованное сотрудничество между учащимися и педагогом. Данная работа посвящена изучению учебного сотрудничества учащихся среднего звена с целью использования этого способа для решения важных вопросов учебного процесса: гуманного подхода к детям, достижения высокой продуктивности учебной деятельности, повышения качества знания учащихся.
Для достижения поставленной цели необходимо решить следующие задачи:
− обосновать выбор направления работы;
− раскрыть актуальность педагогики сотрудничества;
− описать методику организации сотрудничества в учебно-воспитательном процессе;
− перечислить эффекты педагогики сотрудничества;
− показать реализацию этого способа на практике.
По ФГОС обучение представляет собой создание учебной ситуации, в которой учащиеся под руководством учителя определяют предмет своего действия, исследуют его, ставят цели своей деятельности и планируют ее. В связи с этим изменяется структура урока и действия учителя и ученика. На всех этапах урока должна проявляться самостоятельность учащихся. Урок должен быть проблемным и развивающим. Учитель сам нацеливается на сотрудничество с учениками и умеет направлять учеников на сотрудничество с учителем и одноклассниками. В учебном процессе учитель выступает в роли организатора, а не информатора. Важно стимулировать учебную самостоятельность детей. Для достижения поставленной цели ученики не должны получать новые средства и готовые способы действия. Их необходимо подвести к открытию новых законов, правил, после чего возникает желание — найденный способ проверить на практике.
Одной из предложенных форм работы с детьми, способствующих их общему развитию, является сотрудничество. Ведущим психологом Л. В. Занковым сказано, что то, что ребенок умеет делать сегодня в сотрудничестве, завтра он сумеет сделать самостоятельно.
Представление о пути воздействия обучения на развитие ребенка раскрывается благодаря введенному Л. С. Выготским различению двух уровней развития ребенка. Первый — это уровень актуального развития, когда ребенок самостоятельно решает задачи. Второй уровень Л. С. Выготский назвал зоной ближайшего развития, когда ребенок в состоянии решить задачи только с помощью взрослого или своего товарища в коллективной деятельности по подражанию. Значит, нам педагогам необходимо создавать для учащихся в школе атмосферу сотрудничества, то есть успеха и радости. Это свидетельствует об актуальности выбранной темы и исследовательской работы.
Задача учителя научить своих учеников учиться, учиться самостоятельно, добывать знания. Умение учиться — это новообразование, связанное в первую очередь с освоением формы учебного сотрудничества. Нам следует организовать педагогический процесс таким образом, чтобы учащиеся были не объектом, а субъектом учебной деятельности. По словам А. Соловейчика задача учителя учить всех детей, сохраняя достоинство каждого и создавая условия комфорта. Это можно достичь через организацию учебного сотрудничества.
Для проверки выдвинутой гипотезы в том, что правильно организованное сотрудничество является наиболее эффективной формой работы с учащимися, мной было проведено следующее:
− изучение специальной литературы, раскрывающей методику организации сотрудничества;
− разработка системы уроков с использованием разных видов сотрудничества;
− наблюдение за поведением детей на уроках во время коллективного способа обучения;
− сравнение усвоения учебного материала при традиционных формах работы и при коллективном способе обучения;
− анализ школьной успеваемости учащихся класса для оценки успешности усвоения школьной программы;
− собеседования с родителями для получения всесторонних данных об успешности учащихся;
− тестирование детей до и после проведения системы уроков с использованием сотрудничества с целью проверки сформированности учебной мотивации по рисуночному тесту «В школе» и сформированности мыслительных процессов — по методике Переслени;
− анкетирование учащихся для выяснения их познавательного интереса.
Формы организации сотрудничества, используемые мной в работе с детьми, следующие: сотрудничество в паре, когда одного говорящего слушает только один человек; сотрудничество в группах (с 4–5-7-учениками), когда один сразу учит одновременно несколько человек; сотрудничество в парах сменного состава, когда с каждым общаются по очереди и отдельно.
Могут быть выполнены следующие работы в парах на уроках математики: выполнение различных упражнений (устных и письменных), решение задач и выражений, взаимообмен заданиями, работа по вопросникам, разгадывания ребусов, кроссвордов, работа с дидактическим материалом, работа по вопросникам.
Продуктивно проходит работа по вопроснику в парах. Вопросники составляются по пройденному материалу. Они помогают закрепить в памяти теоретический материал. Вопросник есть у каждого ученика. Учитель называет номер вопроса, они проверяют друг у друга знания ответа на этот вопрос. Если товарищ не знает, то ему помогает партнер или же советует посмотреть по учебнику (это допускается). Групповую работу с детьми, как и работу в парах, использую на всех этапах урока.
Примерный план проведения групповых занятий таков:
- Вводная часть:
- постановка познавательной цели;
- инструктаж о последовательности работы;
- раздача дидактического материала по группам.
- Работа групп:
- знакомство с материалами, планирование работы в группе;
- распределение заданий внутри группы;
- индивидуальное выполнение задания;
- обсуждение индивидуальных результатов работы в группе;
- обсуждение общего задания в группе;
- подведение итогов.
- Заключительная часть:
- сообщение о результатах работы в группах;
- анализ выполнения познавательной задачи;
- общий вывод о работе групп и достижении поставленной задачи (решение проблемной ситуации).
Групповую форму работы с детьми применяю при решении различных выражений и задач на уроках математики. Она помогает выйти ребятам из проблемной ситуации.
При изучении темы урока: «Умножение разности двух выражений на их сумму» (Получение формулы сокращенного умножения), 7 кл. Перед ребятами была поставлена проблема. Ее решение происходило коллективным способом. Предметом исследования являлось произведение (a-b)(a+b), то есть следует умножить разность двух выражений на их сумму. Урок проходил в нестандартной форме, в классе был создан научно-исследовательский институт. К каждой лаборатории был представлен план работы на карточке. Было рекомендовано всем сотрудникам действовать сообща, воспользоваться теоретическими знаниями, выполнять некоторые преобразования, приложить все умения, и тогда обязательно свершится новое открытие.
Содержание карточки по плану работы:
− умножить разность a-b на сумму a+b
− приведите подобные слагаемые, если они есть.
− запишите, какое тождество получили.
− сделайте вывод, чему равно произведение разности суммы двух выражений.
После выполнения всей работы сотрудники каждой лаборатории делают вывод, что произведение разности двух выражений и их суммы равно разности квадратов двух этих выражений. Ученики объясняют решения, как выполняли, а учитель пишет на доске. Все записывают в тетрадь выражение (a-b)(a+b)=
+ba-ba-
=
-. Далее проводится проверка установленной закономерности у доски. К доске выходит один ученик и комментирует решения следующего выражения (2x-3)(2x+3)+4
+6x-6x-9=4-9=(2)- 
. В итоге все лаборатории сообщают о получении новой формулы сокращенного умножения, и каждый представляет свою итоговую работу на листе формата А4, где написано (a-b)(a+b)=-.
При закреплении материала тоже проводится работа в группе с проверкой. Например, дается задание № 912. Выполнить умножение. Перед этим дается задание сравнить, чем отличается выражения. Снова предлагается карточка с заданием для каждой лаборатории.
- (a-b)(a+b);
- (a+b)(a-b);
- (a-b)(b+a).
В результате коллективного обсуждения каждая лаборатория делает выводы:
Во втором выражении множители переставлены на основе переместительного свойства умножения, в третьем выражении во втором множители, представляющего в виде суммы, переставили местами слагаемые на основе переместительного закона сложения.
В итоге выражения 1, 2, 3 равны, значит, все части будут равны -
так как все выполнялось строго по математическим законам. Снова все лаборатории представляю свой результат на ватмане.
(a-b)(a+b)=-;
(a+b)(a-b)=-;
(a-b)(b+a)=-.
Далее продолжается выполнение работы в группе задания № 912 с учетом, сделанных вначале выводов.
Со стороны учителя, который является руководителем всех лабораторий, ведется наблюдение, как выполняется данное задание и при необходимости даются некоторые рекомендации. Учитель анализирует, как принимает участие в работе каждый из сотрудников лаборатории.
Далее после выполнения всей работы проводится взаимопроверка. Одной из групп, которая завершила первой работу, представляется возможность изложить свое решение. Все остальные проверяют, учитель отмечает правильность выполнения работы.
На уроках кроме групповой формы используется работа в парах, взаимопроверка и самоконтроль. Методы коллективного способа обучения используются на многих уроках. Выше предложено было использование этого метода на одном из уроков алгебры 7 класса.
В итоге в результате систематического использования выше перечисленных форм работы на уроках математики получены следующие результаты (Рис. 1.).
Данные Рис.1 показывают продвижение детей вперед в развитии ума, воли и чувств. Качество знаний возросло с 68 % до 85 %. В беседе с родителями, через анкетирование, выяснили, что дети лучше знают тот материал, который изучали в классе коллективно. При анкетировании 96 % детей назвали математику интересным и любимым предметом. Возросла самостоятельность и организованность детей, сплоченность всего класса. Отсюда вытекает, что правильно организованное сотрудничество дает хорошие результаты в учебно-воспитательном процессе. Возрастают и объем усваиваемого материала, и глубина его понимания, не остается учеников, не работающих на уроке, ученики комфортнее чувствуют себя в школе. Эти выводы о роли сотрудничества в обучении подтверждают слова Ш. А. Амонашвили. По его словам, сотрудничать, значит, «сделать ребенка добровольным и заинтересованным сотрудникам, единомышленником в своем же воспитании, образовании, обучении…».
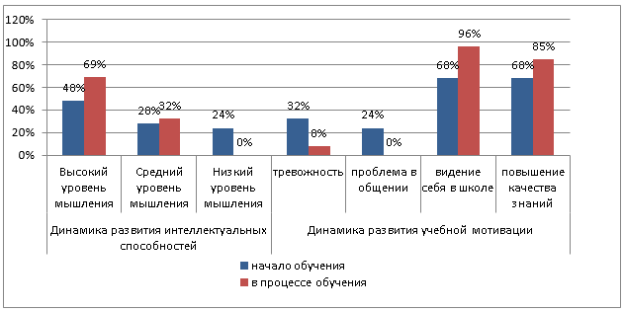
Рис. 1.
Литература:
- Алгебра. 7 класс. Самостоятельные работы для учащихся общеобразовательных организаций: к учебнику А. Г. Мордковича/ Л. А. Александрова; под ред. А. Г. Мордковича, — 11 –е изд., стер. — М.: Мнемозина, 2015. — 112 с.: ил.
- Алгебра. 7 класс. В 2 Ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений/ А. Г. Мордкович/ Н. П. Николаев. — 4 –е изд., стер. — М. Мнемозина, 2012. — 192 с.: ил.
- Активизация мыслительной деятельности учащихся при изучении математики. А. Д. Семушкин и др. Пособие для учащихся. — М.: «Просвещение», 1978.
- Виды учебной деятельности школьников в дистанционном обучении. Г. А. Андрианова. — Интернет-журнал «Эйдос». — 2004. — Режим доступа: http:// www.eidos.ru/journal/2001/0516.htm
- Воспитание интереса к знаниям и потребности к самообразованию. Книга для учителя. В. Б. Бондаревский. — М.: «Просвещение», 1985.
- Диагностические степени обученности учащихся. Учебно-справочное пособие. В. П. Симанов. — М.: пед. университет. — факт.: повышение квалификации преподавателей вузов. — 1999. – 45 с.
- Избранные педагогические труды. Занков Л. В. — 3-е изд., дополн. — М.: «Дом педагогики», 1999. — 608 с.
- Проектирование современного урока в соответствии с требованиями ФГОС ООО: методическое пособие/авт.-сост: С. В. Фаттахова. Казань, 2015, 90 С.
- Проблема культурного развития ребенка из книги: (Выготский Л. С. Психология развития человека. — М.: Изд-во Смысл; Эксмо, 2005. — 1136 с.).
- Справочник учителя математики. Н. А. Ким. — Волгоград: «Учитель», 2012.
- Учитель учится математики. Л. И. Фридман. Книга для учащихся. М.: «Просвещение», 1985.
- Видеоконференция «Разные грани профессионального мастерства педагога». А. С. Соловейчик. Режим доступа: 22.06.2016.
