Цель данной работы заключается в разработке оптимального алгоритма нечеткого поиска по словарю для базы данных.
В ходе выполнения работы был реализован алгоритм поиска на основе хэширования. Основная метрика, которая применялась для сравнения строк — расстояние Левенштейна. Данный алгоритм должен быть достаточно эффективным, чтобы сократить время поиска, так как метрика Левенштейна имеет квадратичную сложность.
Все алгоритмы были реализованы в Ruby 2.2.4, графики были выполнены в программе Matlab 2010.
Ключевые слова: нечеткий поиск, расстояние Левенштейна, хэширование
В данной работе будет предложен алгоритм поиска наиболее близких значений из словаря к входному запросу. Некоторые выводы, используемые в работе, были основаны на результатах работ Бойцова Л. М. [1], т. к. в своих статьях он уже проводил сравнения основных алгоритмов и повторение полученных им результатов является нецелесообразным.
Общая проблематика нечеткого поиска.
Под нечетким поиском понимается поиск по ключевым словам с учётом возможных произвольных ошибок в написании ключевого слова или, напротив, ошибок написания слова в целевом запросе.
Ключевым моментом построения грамотного поиска является выбор меры сходства между словами или, как еще принято называть, функции расстояния между словами, которую будем называть метрикой.
Другим важным аспектом является правильная индексация элементов для быстрого и надежного поиска. Применение метрик сравнения слов достаточно ресурсоемкая операция, поэтому необходимо выделять подмножество исходного словаря, которое может содержать элементы поискового запроса.
Выбор метрики сравнения слов.
Наиболее распространенной метрикой является метрика Левенштейна. Расстояние Левенштейна — это наименьшее расстояние редактирования такое, что одна строка переходит в другую. Данная метрика очень популярна и используется повсеместно, поэтому не будем останавливаться на ней подробно.
В случае сравнения строк, предпочтительней высчитывать расстояние для каждого слова отдельно, а не для строки целиком. Более того, необходимо выполнить нормировку, чтобы оценить коэффициент схожести слов. В нашем случае данный коэффициент будет вычисляться по следующей формуле:
,
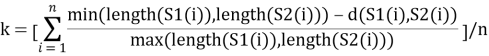где d(S1(i),S2(i)) расстояние Левенштейна, n — кол-во слов в строке (обычно для ФИО n=3); S1,S2 состоят из последовательности слов, поэтому вычисляем расстояние Левенштейна для каждой пары слов; k — показывает схожесть двух последовательностей слов (два ФИО).
Метод индексирования словаря.
Вычисление расстояния Левенштейна имеет квадратичную сложность, поэтому очень важно выбрать в исходном словаре множество, которое могло бы содержать исходный запрос. подобные методы основаны на сэмплировании, т. е. выделении характерных элементов строк. Наиболее подходящим методом для небольшой базы данных (до 500000 тыс. элементов словаря) является хэширование по сигнатуре [1]. Данный подход обеспечивает наилучшее соотношение качества поиска и скорости обработки запроса. Он имеет преимущество по сравнению с другими методами, такими как soundex (метафон), n-грамм, поиск по дереву, так как позволяет допускать ошибки в произвольных частях слова и при этом качество поиска не ухудшиться. Это имеет существенное значение при переводе русских имен на латиницу. Более того, такой метод ускорения поиска подходит для любого языка. Примером такой функции может быть 
. Такая функция была предложена в статье [5]. Данная функция хорошо подходит при считывании словаря с дискового пространства, но так как в нашем случае весь словарь будет загружен в оперативную память, то наиболее подходящим вариантом будет следующая формула: 
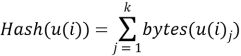, u(i) — элемент словаря, k=length(u(i)). Мы просуммируем все уникальные значения кодов символов строки и получим некий образ. Таким образом, мы построим сюръективное отображение множества элементов словаря в некий набор образов и получили вектор столбец 
, где n — размер словаря
Описание используемого алгоритма исравнение результатов.
Поисковый алгоритм будет реализован следующим образом:
- словарь сортируется по возрастанию значений h(i) — значений хэшей
-
û(1):
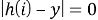, где y — образ входного запроса
- k=koeff(u(i),a), — вычисляем коэффициенты схожести; если нашли элементы с k=1.0, то поиск завершаем.
-
û (2)=
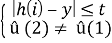, t=max(bytes(char)) — максимальное значение кода символа
и так далее. Расширять выборку подмножества мы будем ограниченное число раз, равное максимально допустимому числу ошибок вставки или удаления. Переменная t на каждом шаге увеличивается, т. е. вначале мы ищем на точное совпадение образов (t=0*t), далее t=t*1 и ищем элемент в этом множестве (без элементов предыдущего) и так далее, расширяя максимально допустимое число раз.
Используя подобный метод индексирования и применяя метрику Левенштейна, можно добиться следующих результатов. На рисунке представлено сравнение скорости поиска без индексирования и с использованием метода индексирования предложенного в нашей работе. Для точности результатов использовался входной набор из 20 элементов (20 запросов для каждого размера словаря) и замерялось время.
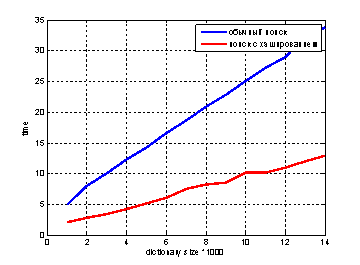
Рис. 1 Сравнение временных затрат для обычного поиска и поиска с хэшированием
Мы видим, что с увеличением размера словаря, выигрыш становится существенен. Более того, в данном примере рассматривался случай, когда словарь не содержит искомый запрос и допустимо 3 ошибки. В реальной ситуации поиск, с предложенным алгоритмом, будет занимать значительно меньше времени.
Теперь сравним алгоритмы поиска с использованием функции хэширования из статьи Бойцова Л. М. [5] и используемой в работе (при сравнении рассматриваем ситуацию, что элемент в словаре отсутствует и допустимо 3 ошибки, входной набор состоит из 20 запросов).
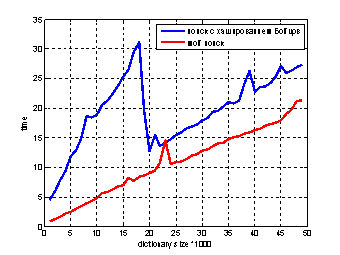
Рис. 2 Сравнение временных затрат поиска с использованием функции Бойцова и предложенной в статье
Исходя из графика, видим, что наш метод показал лучшие результаты. Более того, алгоритм был внедрен в локальную базу данных и успешно используется. Он обеспечивает быстрый и качественный поиск.
Литература:
- Бойцов Л. М. «Классификация и исследование современных алгоритмов нечеткого словарного поиска» // Труды 6-ой Всероссийской научной конференции “Электронные библиотеки: перспективные методы и технологии, электронные коллекции” — RCDL2004, Пущино, Россия, 2004.
- Бондаренко А. В., Визильтер Ю. В., Клышинский Э. С., Силаев Н. Ж., Максимов В. Ю., Мусаева Т. Н. «Формальный метод нечеткого поиска персональной информации», Препринты ИПМ им. М. В. Келдыша, 2009, 064, 25 с. URL: http://library.keldysh.ru/preprint.asp?id=2009–64
- Дональд Кнут «Искусство программирования», том 1, Основные алгоритмы, Вильямс, 2015
- Фултон Х., Арко А. «Путь Руби», ДМК Пресс, 2016
- Бойцов. Л.М. «Использование хеширования по сигнатуре для поиска по сходству», ВМиК МГУ, № 8 стр. 135–154, 2001.
