Блочно-операторные матрицы — это матрицы, элементы которых являются линейными операторами, определенными между банаховым или гильбертовым пространством. Такие операторы возникают в статистической физике, теории твердого тела, теории химических реакции, магнито-гидродинамике, квантовой механике и т. д. Недавно в монографии [1] подробно изучены абстрактные свойства ограниченных и неограниченных блочно-операторных матриц и их применения в некоторых задачах математической физики.
В настоящей работе рассматривается блочно-операторная матрица ![]() действующая в так называемом двухчастичном обрезанном подпространстве Фоковского пространства. Описан дискретный спектр оператора
действующая в так называемом двухчастичном обрезанном подпространстве Фоковского пространства. Описан дискретный спектр оператора ![]() и задача состоит в обосновании этих описаний.
и задача состоит в обосновании этих описаний.
Отметим, что оператор ![]() можно рассмотреть как одномерное возмущение оператора
можно рассмотреть как одномерное возмущение оператора ![]() , рассмотренного в работах [2, 3], где изучены пороговые явления для оператора
, рассмотренного в работах [2, 3], где изучены пороговые явления для оператора ![]() .
.
Пусть ![]() — компактное связанное множество,
— компактное связанное множество, ![]() - гильбертово пространство квадратично интегрируемых (комплекснозначных) функций, определенных на
- гильбертово пространство квадратично интегрируемых (комплекснозначных) функций, определенных на ![]() и
и ![]() — одномерное комплексное пространство.
— одномерное комплексное пространство.
Обозначим
![]()
Гильбертово пространство ![]() называется трехчастичным обрезанным подпространством Фоковского пространства.
называется трехчастичным обрезанным подпространством Фоковского пространства.
Рассмотрим блочно-операторную матрицу ![]() , действующую в гильбертовом пространстве
, действующую в гильбертовом пространстве ![]() и задающуюся как
и задающуюся как
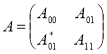 , (1)
, (1)
где матричные элементы ![]() определяются по формулам
определяются по формулам
![]()
Здесь ![]()
![]() — фиксированное вещественное число,
— фиксированное вещественное число, ![]() — вещественнозначные непрерывные (ненулевые) функции на
— вещественнозначные непрерывные (ненулевые) функции на ![]() . Здесь и в дальнейшем интеграл без указания пределов всюду означает интегрирование по всей области изменения переменных интегрирования.
. Здесь и в дальнейшем интеграл без указания пределов всюду означает интегрирование по всей области изменения переменных интегрирования.
В современной математической физике оператор ![]() называется оператором уничтожения, а оператор
называется оператором уничтожения, а оператор ![]() называется оператором рождения, см. [4]. Оператор уничтожения снижает количество частиц в заданном состоянии на единицу, а оператор рождения увеличивает число частиц в данном состоянии на единицу, и является сопряженным к оператору уничтожения. Такие операторы имеют широкое применение в квантовой механике, в частности, в изучении квантовых гармонических осцилляторов и систем многих частиц.
называется оператором рождения, см. [4]. Оператор уничтожения снижает количество частиц в заданном состоянии на единицу, а оператор рождения увеличивает число частиц в данном состоянии на единицу, и является сопряженным к оператору уничтожения. Такие операторы имеют широкое применение в квантовой механике, в частности, в изучении квантовых гармонических осцилляторов и систем многих частиц.
Легко можно проверить, что оператор ![]() , определенный операторной матрицей (1) и действующий в гильбертовом пространстве
, определенный операторной матрицей (1) и действующий в гильбертовом пространстве ![]() , является ограниченным и самосопряженным.
, является ограниченным и самосопряженным.
Следует отметить, что оператор типа (1) является оператором, носящим название обобщенной модели Фридрихса. Как таковая, обобщенная модель Фридрихса введена в работе [5], где были изучены ее собственные значения и «резонансы» (особенности аналитического продолжения резольвенты). А в работе [6] оно рассматривается как двухканальная молекулярно-резонансная модель.
Обозначим через ![]() и
и ![]() , соответственно, существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
, соответственно, существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
Пусть оператор ![]() действует в
действует в ![]() как
как
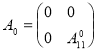
Оператор возмущения ![]() оператора
оператора ![]() является ограниченным самосопряженным оператором ранга не более чем 3. Следовательно, из известной теоремы Г. Вейля (см. [7], теорема XIII.14) о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр оператора
является ограниченным самосопряженным оператором ранга не более чем 3. Следовательно, из известной теоремы Г. Вейля (см. [7], теорема XIII.14) о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр оператора ![]() совпадает с существенным спектром оператора
совпадает с существенным спектром оператора ![]() . Известно, что
. Известно, что
![]()
где числа
![]()
Из последних двух фактов следует, что
![]()
Сформулируем основные результаты работы.
Теорема 1.Оператор![]() может иметь не более двух (не более одного) простых собственных значений, лежащих левее
может иметь не более двух (не более одного) простых собственных значений, лежащих левее ![]() (правее
(правее ![]() ).
).
Далее, для формулировки второго результата работы вводим операторы
![]() и
и 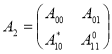 .
.
Из определения операторов ![]() видно, что они имеют более простую структуру чем
видно, что они имеют более простую структуру чем ![]() .
.
Теорема 2. Если один из операторов ![]() или
или ![]() имеет собственное значение
имеет собственное значение ![]() тогда оператор
тогда оператор ![]() имеет единственное простое собственное значение на
имеет единственное простое собственное значение на ![]()
Литература:
- C. Tretter. Spectral Theory of Block Operator Matrices and Applications. ImperialCollegePress, 2008.
- Т. Х. Расулов. О существовании виртуального уровня обобщенной модели Фридрихса. Узбекский Математический Журнал. 2007, № 4, стр. 56–63.
- Т. Х. Расулов. О собственных значениях обобщенной модели Фридрихса. Узбекский математический журнал, 2006, № 4, стр. 61–68.
- К. О. Фридрихс. Возмущения спектра операторов в гильбертовом пространстве. М.: Мир, 1972.
- С. Н. Лакаев. Некоторые спектральные свойства модели Фридрихса. Труды семинара им. И. Г. Петровского, 11 (1986), 210–223.
- A. K. Motovilov, W. Sandhas, Y. B. Belyaev. Perturbation of a lattice spectral band by a nearby resonance. J. Math. Phys., 42 (2001), 2490–2506.
- М. Рид, Б. Саймон. Методы современной математической физики, т. 4. Анализ операторов, М.: Мир. 1982.







