Ключевые слова: квадрокоптер, система управления, пространство состояний, LQR, асимптотические наблюдатели, регулятор
Данная статья основана на работе с математической моделью БПЛА с четырьмя несущими винтами, вращающимися в диагонально противоположных направлениях. Данная математическая модель представляет собой совокупность SISO-подсистем, полученных путем линеаризации и декомпозиции системы, выведенной в [1]. Для построения закона управления используется технология LQR-синтеза, описанная в [2]. Полученный регулятор посредством имитационного моделирования в пакете прикладных программ MATLAB & Simulink сравнивается с регулятором, синтезированным при помощи MIMO-системы до ее декомпозиции.
Основным объектом данной работы является совокупность SISO-подсистем (1), полученная из модели динамики квадрокоптера вида (2), представленной в [1], путем линеаризации в окрестности положения равновесия (3) и последующей декомпозиции, основанной на предположениях (4) о виде управляющего сигнала.
![]() .(2)
.(2)
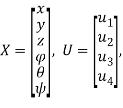
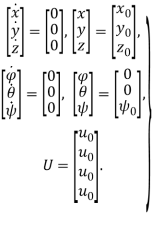 (3)
(3)
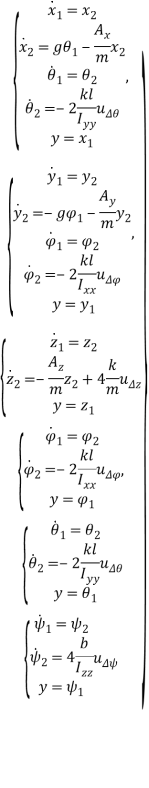 (1)
(1)
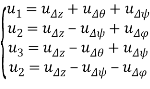 .(4)
.(4)
Здесь управляющий сигнал ![]() представляет собой квадрат угловой скорости винта -го мотора квадрокоптера,
представляет собой квадрат угловой скорости винта -го мотора квадрокоптера, ![]() — координаты центра масс квадрокоптера в абсолютной системе координат,
— координаты центра масс квадрокоптера в абсолютной системе координат, ![]() — углы Эйлера, представляющие собой ориентацию квадрокоптера (крен, тангаж и рысканье соответственно). Значение
— углы Эйлера, представляющие собой ориентацию квадрокоптера (крен, тангаж и рысканье соответственно). Значение ![]() находится из уравнения вертикальной динамики квадрокоптера с допущением, что при данной величине управляющего сигнала БПЛА висит в воздухе неподвижно (по оси
находится из уравнения вертикальной динамики квадрокоптера с допущением, что при данной величине управляющего сигнала БПЛА висит в воздухе неподвижно (по оси ![]() ) в горизонтальном положении:
) в горизонтальном положении:
![]()
Таким образом, значение управляющего сигнала
![]()
где ![]() — масса квадрокоптера,
— масса квадрокоптера, ![]() — сила тяжести и
— сила тяжести и ![]() — коэффициент тяги моторов. Подробнее с исходной нелинейной моделью квадрокоптера (а так же с ее выводом) вы можете ознакомиться в [1]. Величины
— коэффициент тяги моторов. Подробнее с исходной нелинейной моделью квадрокоптера (а так же с ее выводом) вы можете ознакомиться в [1]. Величины ![]() определяются следующим соотношением:
определяются следующим соотношением:
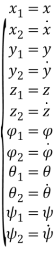
Для построения законов управления для совокупности подсистем (1) воспользуемся LQR-синтезом. Данный метод подразумевает собой модальный синтез с условием, что корни системы располагаются так, чтобы минимизировать функционал (5), отвечающий за оптимальное энергопотребление при желаемом быстродействии.
Пусть имеется SS-модель:
![]()
с линейной обратной связью ![]() .
.
Синтез управления заключается в решении задачи оптимизации (5) относительно SS-системы.
![]() (5)
(5)
Матрицы ![]() задаются, обычно, таким образом, чтобы регулятор удовлетворял желаемой динамике. Чем больше значения коэффициентов
задаются, обычно, таким образом, чтобы регулятор удовлетворял желаемой динамике. Чем больше значения коэффициентов ![]() относительно коэффициентов
относительно коэффициентов ![]() , тем интенсивнее будет управляющий сигнал.
, тем интенсивнее будет управляющий сигнал.
Матрица
![]() .
.
Методология LQR-синтеза требует полной измеряемости вектора состояния, а SISO-система по своей сути не обеспечивает полноты набора измеряемых величин, если вектор состояния состоит более чем из одной компоненты. Для удовлетворения этого требования следует построить и объединить с регулятором асимптотический наблюдатель. Система наблюдателя
![]() (6)
(6)
Входным сигналом является вектор измерений ![]() , вектор
, вектор ![]() системы (6) является оценкой вектора состояния системы, для которой строится наблюдатель. Коэффициенты вектора
системы (6) является оценкой вектора состояния системы, для которой строится наблюдатель. Коэффициенты вектора ![]() выбираются таким образом, чтобы обеспечивать устойчивость системы. Закон управления, в таком случае, будет иметь вид:
выбираются таким образом, чтобы обеспечивать устойчивость системы. Закон управления, в таком случае, будет иметь вид:
![]() (7)
(7)
Замкнув наблюдатель (6) обратной связью (7), получим систему-регулятор:
![]() .(8)
.(8)
Решим, теперь, для каждой подсистемы задачу (5) при помощи пакета прикладных программ MATLAB. За параметры БПЛА примем значения (подробнее о параметрах в [1]):
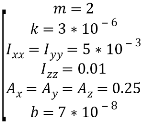 .
.
Матрицы ![]() и
и ![]() подобраны, исходя из требований к динамике регулятора и его технических возможностей, следующими:
подобраны, исходя из требований к динамике регулятора и его технических возможностей, следующими:
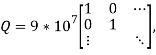
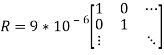 .
.
Для анализа синтезированных регуляторов в среде MATLAB & Simulink была построена нелинейная модель динамики квадрокоптера, изложенная в [1]. Полученная система управления сравнивалась с другой, LQR-регулятор которой был получен, основываясь на MIMO-системе (до декомпозиции). Для реализации тестовых режимов имитационного моделирования вектора желаемого состояния системы брались следующими:
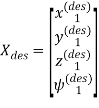 .(9)
.(9)
Остальные компоненты всегда вектора считались нулевыми.
В ходе имитационного моделирования было выяснено, угол ![]() вносит существенную нелинейность в динамическую модель. Данный фактор не может быть учтен регулятором, в основе которого лежит LQR-синтез и вызывает потерю устойчивости системы, если пытаться одновременно стабилизировать компоненты
вносит существенную нелинейность в динамическую модель. Данный фактор не может быть учтен регулятором, в основе которого лежит LQR-синтез и вызывает потерю устойчивости системы, если пытаться одновременно стабилизировать компоненты ![]() и
и ![]() . Поэтому, для достижения (9) нужно сначала стабилизировать положение
. Поэтому, для достижения (9) нужно сначала стабилизировать положение
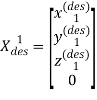 ,(10)
,(10)
а уже после этого вводить ![]() в вектор (10).
в вектор (10).
Если же в качестве желаемого положения задавались значения, непрерывно изменяющиеся с течением времени, образуя траекторию:
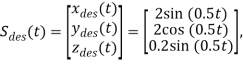 (11)
(11)
то оба регулятора успешно справлялись с поставленной задачей, приводя, квадрокоптер на окружность и успешно по ней перемещая (рис. 1). При таком режиме движения различия между траекториями крайне незначительны и могут быть оценены следующим выражением:
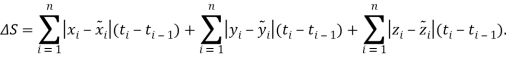
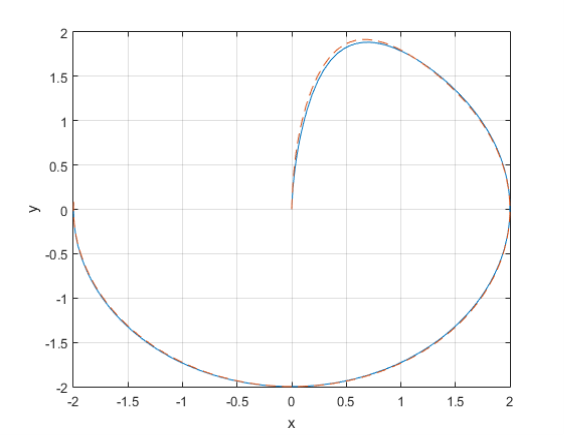
Рис. 1. Проекция траекторий моделей квадрокоптеров на плоскость ![]()
При желаемой траектории движения (11) и времени моделирования ![]() сумма
сумма ![]() имела значение 0.015.
имела значение 0.015.
На основании данного результата можно сделать вывод, что оба LQR-регулятора применимы к нелинейной модели квадрокоптера, при условии, что стабилизация желаемого значения угла рысканья ![]() вынесена в отдельный режим с наименьшим приоритетом. Регулятор, построенный применительно к системе (1) может быть использован как альтернатива обычному LQR-регулятору в вопросах об анализе робастности данного типа регуляторов, поскольку в данном случае предстоит работать с шестью передаточными функциями, вместо двадцати четырех.
вынесена в отдельный режим с наименьшим приоритетом. Регулятор, построенный применительно к системе (1) может быть использован как альтернатива обычному LQR-регулятору в вопросах об анализе робастности данного типа регуляторов, поскольку в данном случае предстоит работать с шестью передаточными функциями, вместо двадцати четырех.
Литература:
- Luukkonen T., Modelling and control of quadcopter, 2011, P.2–6.
- Веремей Е. И., Линейные системы с обратной связью: учебное пособие. 2013, с. 280–290,372–384.







