К расчёту переходных процессов в линейных электрических цепях с помощью графов переменных состояния

Article is devoted calculation of transients in linear electric chains by a method of space of parameters of a condition in which the matrix of transition of a chain and transitive curves are defined by optimum way in the computing plan: by the form counts of variables of a condition. It is shown, that at calculation of chains of a high order, it is recommended for chains not above the third order. If the electric chain is described by system of the equations of higher order definition of a matrix of transition becomes bulky, and only for some special cases the problem dares rather simply. Signal counts are an effective remedy, giving the chance realization of logical sequence of actions at the decision of the joint linear equations describing a condition of an electric chain. The method of counts of variables of a condition is a strict and exact method of calculation of transients in linear electric chains with the concentrated parameters.

Алгоритм расчёта переходных процессов в линейных электрических цепях с сосредоточенными параметрами R,L,C методом пространства параметров состояния, как известно [1], состоит из следующих шагов:

1. По виду докоммутационной схемы с учётом законов коммутации определяются независимые начальные условия цепи: i_L(0) и u_C(0).
2. Для послекоммутационной схемы записываются уравнения по законам Кирхгофа или по методу контурных токов.
3. Выбираются: а) переменные состояния цепи, в качестве которых оптимально брать токи в индуктивностях и напряжения на ёмкостях, определяющих общий порядок системы дифференциальных уравнений цепи; б)переменные управления или входа, ими могут служить э. д.с. и токи источников питания; в) переменные выхода, за которые можно принять токи в активных сопротивлениях и ёмкостях, напряжения на активных сопротивлениях и индуктивностях.
4. Исходные дифференциальные уравнения приводятся к канонической форме записи, т. е. представляются решёнными относительно первых производных переменных состояния по времени и записываются в виде двух основных уравнений метода переменных состояния:

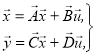(1)

где — матрица переменных состояния размером 1хn (n-порядок цепи);

–матрица входа размером 1хm;

— матрица выхода размером 1хк;

— постоянные матрицы соответствующих размеров, элементы которых зависят только от параметров R,L,C цепи.

5. Рассчитываются общие решения дифференциальных неоднородных матричных уравнений:

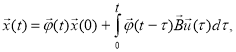(2)

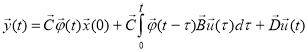, (3)

где — матрица перехода размером nxn, определение элементов которой и составляет главную трудность при использовании данного алгоритма. Вычисление матрицы можно осуществить, в частности, следующими способами [1,2]:

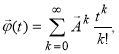(5)

(6)

(7)

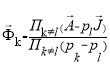где (8)

Другой возможный способ определения вытекает из представления уравнений цепи в виде ориентированного графа — графа переменных состояния и вычисления элементов непосредственно по нему. Кроме наглядности и упрощения процедуры вычисления матрицы перехода здесь достигается также исключение избыточных операций, связанных с неплотностью матриц, т. е. большим количеством нулей в них.

Свободный режим в линейной электрической цепи с постоянными параметрами описывается однородным дифференциальным матричным уравнением

(9)

Прямое преобразование Лапласа обеих частей этого уравнения и приведение подобных слагаемых этого уравнения приводит к выражению

, (10)

откуда получаем формулу расчёта (6) для матрицы перехода .

Покажем это на конкретном примере.

Пусть для некоторой разветвлённой цепи второго порядка составлены однородные дифференциальные уравнения состояния

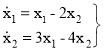
при начальных условиях х₁(0) и х₂(0).

Требуется найти матрицу перехода цепи.

1. Строим граф цепи, переменных состояния цепи:

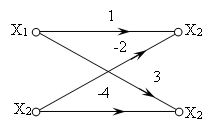
Рис. 1.

Передачами ветвей графа являются элементы основной матрицы цепи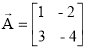

2. Вычисляем матрицу 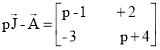и строим граф для изображений и начальных значений переменных состояния, изображающий уравнения (10):

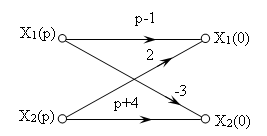
Рис. 2.

3. Выполняем инверсию ветвей с передача р-1 и р+4:

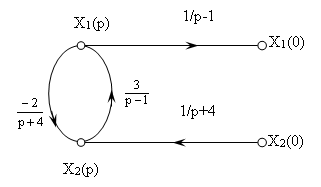
Рис. 3.

4. Исключаем узел Х₂(p) и затем узел Х₁(p):

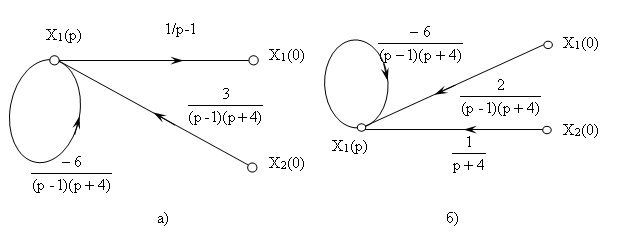
Рис. 4.

5. Исключаем петлю с передачей 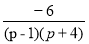и находим изображения элементов матрицы перехода :

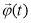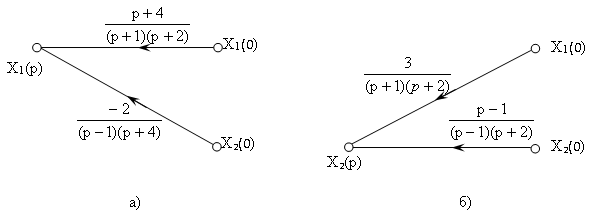
Рис. 5.

6. По виду графов записываем:

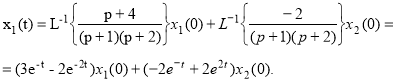
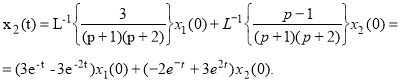
Записываем матрицу перехода

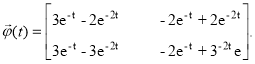
С помощью графа переменных состояния цепи может быть найдена не только матрица перехода , но и рассчитан полностью сам переходный процесс в цепи. Введём вектор-столбец , вектор-столбец и вектор-столбец соответственно для представления переменных состояния процесса, входа и системы увеличенный размерности и получим первое дифференциальное уравнение цепи из системы (1) в виде [2]:

где 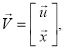— основная матрица цепи увеличенный размерности.

Решение уравнения (11) имеет вид:

(12)

где называется расширенной матрицей перехода цепи, т. к. характеризует одновременно изменение как переменных состояния цепи, так и входа. Если заданы начальные условия, то могут быть легко найдены функции времени, описывающие изменение переменных состояния цепи.

Дополнив граф переменных состояния цепи узлами, соответствующими входным переменным , передачами между переменными состояния и входными переменными, получим граф, изображающий уравнение (11) во временной области.

Для этого необходимо описать с помощью графов и входные воздействия. Ниже показаны графовые модели в переменных состояния для экспоненциальной e(t)=Ee^at, постоянной e(t)=E и синусоидальной э. д.с. e(t)=E_msin(ωt+ψ_e):

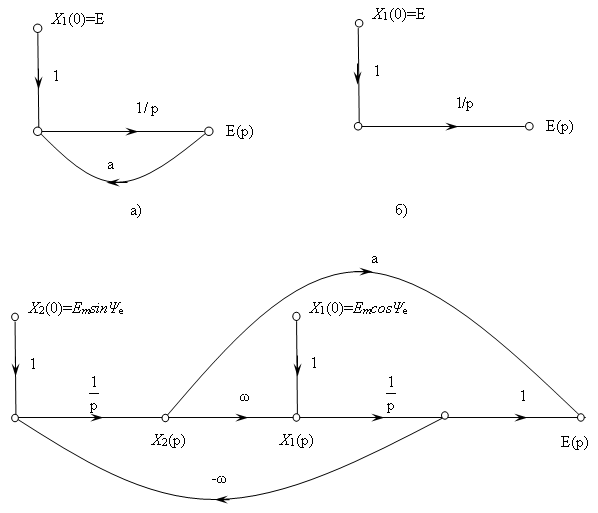
Рис. 6.

Приведём пример расчёта переходных процессов с помощью графов переменных состояния для схемы рис. 7а при e(t) = E = 60 в, R₁ = 20 ом, R₂ = 40 ом; L = 0,2 мГн, С = 1 мкФ, R₃ = 40 ом.

1) Выбрав в качестве переменных состояния напряжение на ёмкости u_C и ток в индуктивности i_L, определим начальные условия и запишем дифференциальные уравнения цепи в переходном режиме:

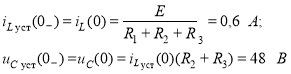
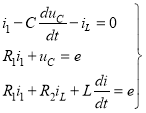(13)

2) Решаем (13) относительно первых производных выбранных переменных состояния u_C и i_L и получаем:

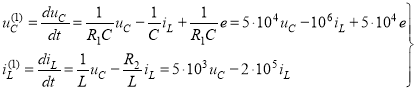(14)

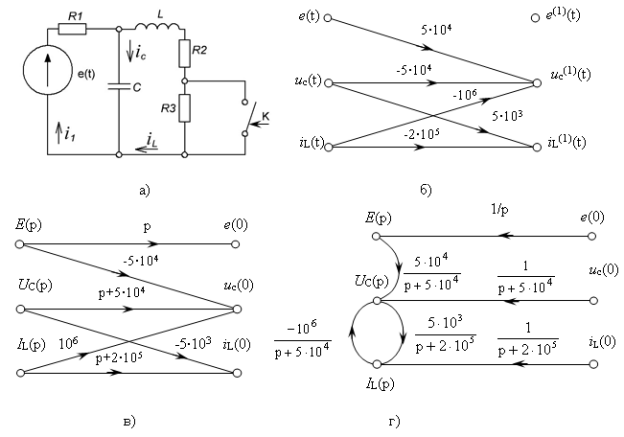
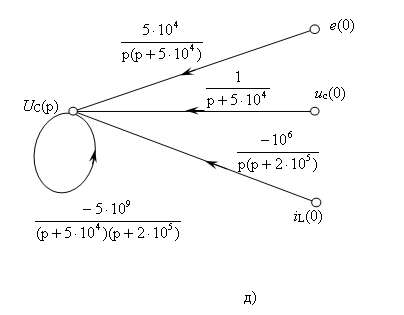
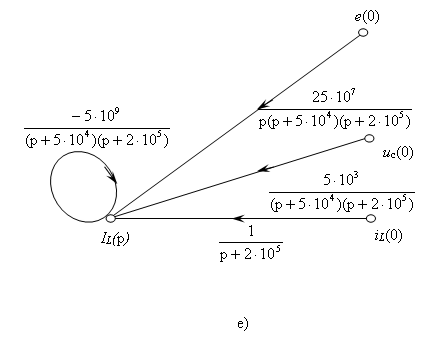
Рис. 7.

3) Граф переменных состояния, соответствующий уравнениям (14), построен на рис. 7б, из рассмотрения которого находим основную матрицу цепи увеличенной размерности:

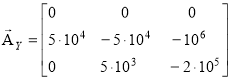
4) Использовав выражение, строим граф изображений переменных состояния (рис. 7в) ∙ Инвертируя ветви с передачами р, (р+5∙10⁴), (р+2∙10⁵) и исключив узлы Е(р) и I_L(р), получим граф рис. 7д, из которого после исключения петли находим:

5) Аналогично из графа рис. 7е определяем изображение тока в ветви с индуктивностью:

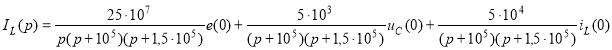
6) Переходя к оригиналам и учитывая, что е(0) = Е = 60 В, u_C(0) = 48 B, i_L(0) = 0,6 A, получим выражения для искомых переменных:

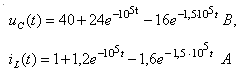
По работе можно сделать следующее заключение: метод графов переменных состояния является строгим и точным методом расчета переходных процессов в линейных электрических цепях с сосредоточенными параметрами.

Сохраняя все достоинства метода пространства переменных состояния, указанный подход является более простым и наглядным, более эффективным в вычислительном отношении. Это становится особенно важным при расчёте цепей высокого порядка, т. к. аналитический метод определения матрицы перехода, необходимый для вывода уравнений состояния методом пространства параметров состояния, можно рекомендовать для цепей не выше третьего порядка. Если электрическая цепь описывается системой уравнений более высокого порядка, то определение матрицы перехода становится громоздким, и только для некоторых частных случаев задача решается сравнительно просто.

Кроме того, метод графов переменных состояния подтверждает известные выводы о том, что сигнальные графы являются эффективным средством, дающим возможность осуществления логичной последовательности действий при решении совместных линейных уравнений, описывающих состояние электрической цепи.

Литература:

1. Демирчян К. С., Нейман Л. Р., Коровкин Н. В., Чечурин В. Л. Теоретические основы электротехники. Учебник для вузов. Том 1. «Питер» Россия 2003.-463 с.
2. Ю.Ту. Современная теория управления. М., Машиностроение, 1971, -300 с.
3. Аmirоv C. F. Yoqubоv M. S., Jаbbоrоv N.G`. Elеktrоtеxnikаni nаzаriy аsоslаri. (birinchi kitоb) TDTU, 2006 y. 144 b.
4. Каримов А. С., Назарий электротехника. -Т.: Ўкитувчи, 2003 й, -426 б.
5. Рашидов Й. Р., Абидов К.Ғ., Колесников И. К. Электротехниканинг назарий асослари I, II, III қисмлар (Маъруза матинлари тўплами), ТДТУ, 2002 й, 250 б.
6. Abidov Q.G`., Qadirova D. R. «Chiziqli elеktr zаnjirlаridа o`tkinchi jаrаyonlаr» bo`yichа hisоb — grаfik ishini bаjаrish yuzаsidаn uslubiy ko`rsаtmа. -Toshkent, ToshDTU, 2010. 36 b.