Преимущества щебеночно-мастичных асфальтобетонов, выявляемые при расчетах на сопротивление сдвигу и усталостному растяжению при изгибе



Преимущества щебеночно-мастичных асфальтобетонов, выявляемые при расчетах на сопротивление сдвигу иусталостному растяжению при изгибе

Жазыбаев Куанышбек Мухаметович, студент

Сибирская государственная автомобильно-дорожная академия

В статье приведены сведения о современных методах расчета асфальтобетонных дорожных покрытий, на основе которых показаны преимущества щебеночно-мастичного асфальтобетона.

Ключевые слова: щебеночно-мастичный асфальтобетон, дорожное покрытие, сдвиг, растяжение при изгибе

Дорожные одежды нежесткого типа, независимо от типа асфальтобетона, используемого в покрытии, рассчитывают по критериям прочности [1]. Такие расчеты объясняют преимущества щебеночно-мастичных асфальтобетонов, проявляемые при упругом прогибе дорожной одежды и растяжении от изгиба. Это несложно продемонстрировать выражениями для расчета срока службы покрытия и дорожной одежды, полученными из критериев прочности [1]. Для вывода этих формул рассмотрим критерии прочности [1].

Расчет асфальтобетонного покрытия на сопротивление усталостному разрушению от растяжения при изгибе выполняется проверкой условия 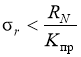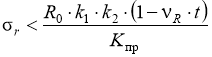[1]:

; (1)

где _r –растягивающее напряжение, МПа; R_N и R₀ — соответственно прочность материала на растяжение при изгибе после приложения N-го числа нагрузки и при ее однократном воздействии, МПа; К_пр — требуемый коэффициент прочности; k₁ — коэффициент, учитывающий снижение прочности вследствие усталостных явлений; k₂ — тоже, но от воздействия погодно-климатических факторов; _R — коэффициент вариации прочности; t — коэффициент нормированного отклонения.

Коэффициент усталости k₁ является функцией суммарного числа расчетных нагрузок N_р и параметров материала а и т. Расчет коэффициента выполняют по формуле:

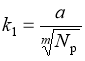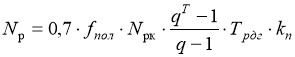; ,(2)

где Т — расчетный срок службы, годы; f_пол — коэффициент, учитывающий распределение движения по полосам проезжей части; N_{рк —} приведенная интенсивность на последний год срока службы, авт./сут; q — показатель изменения интенсивности движения по годам; k_n — коэффициент, учитывающий вероятность отклонения суммарного движения от среднего ожидаемого; Т_рдг – число расчетных дней в году, соответствующих определенному состоянию деформируемости конструкции.

Срок службы покрытия по критерию (1) рассчитывают при помощи решения (1) относительно N_р, а затем, принимая, что N_р определяется по (2), эту зависимость решают относительно T. Выполнив такое решение и приведя полученное выражение к логарифму по основанию 10, получим [2–4]:

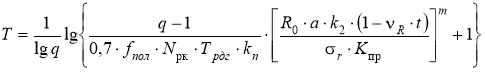(3)

Из формулы (3) следует, что при прочих равных условиях срок службы тем выше, чем больше R₀ и меньше _r, что и обуславливает более высокий срок службы ЩМА по сравнению с другими видами асфальтобетона. Кроме того, для ЩМА разработано большое количество стабилизирующих добавок, служащих для повышения или уменьшения пластичности и ее диаметрально противоположной характеристике хрупкости [5]. Часть таких добавок можно использовать для повышения прочности ЩМА, а значит и срока службы.

Автор отметит, что критерий (1) является первой теорией прочности, или как говорят Галилеевой теории, предложенной в 17 в., и конечно, же являющейся неверной. Более рационально для расчета покрытия по критерию сопротивления растяжению от изгиба применять один из модифицированных критериев прочности, например, модифицированные критерии О. Мора [6, 7] или Писаренко–Лебедева [8, 9], в которых учитываются меры теории накапливания повреждений сплошность Л. М. Качанова или поврежденность Ю. Н. Работнова. Эти меры являются функцией числа расчетных нагрузок, вследствие чего подобны коэффициенту k₁, используемому в выражениях (1) и (3), но определяемые по методам, опубликованным в статьях [10–12]. Из функциональной зависимости эквивалентного напряжения от поврежденности, являющейся функцией числа нагрузок, и параметров материала, можно получить формулу для расчета предельного числа нагрузок. Это предельное число можно подставить в формулу (2) и решить, полученное уравнение относительно срока службы. По сравнению с выражением (3), полученная формула позволит рассчитывать срок службы точнее, но в этой модифицированной формуле сохранится принцип, согласно которому срок службы ЩМА выше, чем других асфальтобетонов.

Для сопоставления сроков службы по критериям колее образования и сопротивления сдвигу ЩМА с другими асфальтобетонами необходимо задействовать научные публикации. Например, в работе [13] показано, что критерий расчета дорожной одежды по ровности можно представить разностью остаточных деформаций, накапливаемых в расчетной точке и в точке, в которой эта деформация имеет минимальное значение. Тогда критерий расчета принимает вид [13]:

(4)

Считается, что пластическое деформирование дискретных материалов, обуславливается сдвигом, который происходит под действием сжимающих напряжений. Аналогичные суждения высказываются об условиях работы асфальтобетонных покрытий большой толщины при высоких летних температурах воздуха [14]. Тогда пластическое смещение материала слоя можно вычислить интегрированием выражения для пластической деформации по толщине этого слоя, а для полупространства по его глубине. Интегральное уравнение имеет вид [1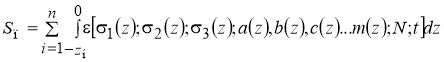5]:

(5)

где i и n — номер и количество слоев дорожной конструкции, включая земляное полотно; z_н — ордината точки, ограничивающей зону распространения пластических деформаций в сечении по оси симметрии нагрузки;  — пластическая деформация, являющаяся функцией рядя параметров материала; ₁(z), ₂(z), ₃(z) — главные напряжения, являющиеся функцией глубины z, Па; a(z), b(z), c(z)…m(z) — параметры материалы, представляющие собой функцию глубины и показателей физических свойств (плотность, влажности, температура, пористость и т. п.); N — Количество приложенных нагрузок; t — время воздействия одной нагрузки, с.

Функциональные зависимости для расчета пластических деформаций дискретных материалов, которые в зависимости (5) являются подынтегральной функцией приведены в работах [16–21]. Аналогичные функции для асфальтобетонов получены в работах [22, 23]. Эти зависимости приведены в табл. 1.

Таблица 1

Функциональные зависимости деформации от числа нагрузок

Математическая модель деформирования	Параметры модели
	1, 1 и 3 — главные напряжения в наиболее опасной точке земляного полотна, Па; ЕПн — нелинейный модуль пластичности к1 и к2 – коэффициенты, учитывающие уровень напряженного состояния.

Для расчета покрытия из ЩМА по сопротивлению сдвигу можно применить условия пластичности, разработанные для грунтов, например критерий Г. К. Арнольда, применяемый Г. В. Долгих для расчета безопасных давлений [24–26] или один из эмпирических критериев [27–31]. Кроме того, можно использовать трехпараметрические критерии Кулона–Мора [32–36], которые прошли апробацию в расчетах асфальтобетонов по сдвигу [8–12], Уравнения предельного состояния по этим критериям даны в табл. 2.

Таблица 2

Уравнения предельного состояния критериев сопротивления сдвигу

Наименование критерия	Уравнение предельного состояния
Эмпирический критерий Г. К. Арнольда [24–26]	, где с и  — сцепление и угол внутреннего трения.
Трехпараметрические критерии Кулона–Мора [8, 12, 32–36]	,.

Выполнив расчеты пластических деформаций и по критерию сопротивления сдвигу несложно убедиться, что срок службы покрытия из ЩМА на 12–27 % выше, чем из других асфальтобетонов. При этом меньшее значение 17 % соответствует ЩМА без стабилизирующих добавок, а более высокие — ЩМА с различными добавками, которые принимались в расчете по рекомендациям [5].

Литература:

1. ОДН 218.046–01. Проектирование нежестких дорожных одежд. – М.: ГСДХ Минтранса России, 2001. — 146 с.

2. Сартаков А. А. Расчет срока службы асфальтогранулобетонных оснований дорожных одежд, восстановленных методом холодного ресайклинга // Высшая школа. — 2016. — № 9. — С. 124–126.

3. Рябков Ю. В. Расчет межремонтных сроков возобновления дорожных одежд методом холодного ресайклинга // Вестник магистратуры. — 2016. — № 5–2 (56). — С. 34–36.

4. Александров А. С. Совершенствование расчета дорожных конструкций по сопротивлению сдвигу. Том Часть 1. Состояние вопроса. — Омск: СибАДИ, 2015. — 292 с.

5. Костин В. И. Щебеночно-мастичный асфальтобетон для дорожных покрытий. — Н. Новгород: ННГАСУ, 2009. — 65 с.

6. Александрова Н. П., Александров А. С., Чусов В. В. Учет поврежденности структуры асфальтобетона в критериях прочности и условиях пластичности // В сборнике: Политранспортные системы материалы VIII Международной научно-технической конференции в рамках года науки Россия — ЕС. Новосибирск: СГУПС, 2015. — С. 219–225.

7. Александрова Н. П., Александров А. С., Чусов В. В. Модификация критериев прочности и условий пластичности при расчетах дорожных одежд // Вестник Сибирской государственной автомобильно-дорожной академии. — 2015. № 1 (41). — С. 47–54.

8. Чусов В. В. Модифицированные критерии Писаренко-Лебедева и Кулона-Мора, учитывающие меры теории накапливания повреждений // Молодой ученый. — 2016. — № 9 (113). — С. 338–341.

9. Чусов В. В. Применение теории накапливания повреждений в условиях пластичности асфальтобетона для расчета дорожных покрытий по сопротивлению сдвигу // Молодой ученый. — 2016. — № 6 (110). — С. 221–227.

10. Aleksandrova N. P. Chysow V. V. The usage of integral equations hereditary theories for calculating changes measures in the theory of damage when exposed to repeated loads // Magazine of Civil Engineering, 2016, No.2. Article in Press.

11. Чусов В. В., Александрова Н. П. Два способа расчета мер теории накапливания // В сборнике: Наука XXI века: опыт прошлого — взгляд в будущее: материала II международной научно-практической конференции — Омск, СибАДИ, 2016 — С. 271–275.

12. Чусов В. В. Прогнозирование изменения мер теории накапливания повреждений при циклической нагрузке // В сборнике: Наука сегодня: глобальные вызовы и механизмы развития: материалы международной научно-практической конференции, г. Вологда, 27 апреля 2016 г. — Вологда: ООО «Маркер», 2016. — С. 53–54.

13. Герцог В. Н., Долгих Г. В., Кузин В. Н. Расчет дорожных одежд по критериям ровности. Часть 1. Обоснование норм ровности асфальтобетонных покрытий // Инженерно-строительный журнал. — 2015. — № 5 (57) — С. 45–57.

14. Чусов В. В. Применение мер теории накапливания повреждений для модификации условия пластичности кулона — мора при расчете асфальтобетонных покрытий // В сборнике: Наука сегодня: глобальные вызовы и механизмы развития: материалы международной научно-практической конференции, г. Вологда, 27 апреля 2016 г. — Вологда: ООО «Маркер», 2016. — С. 50–52.

15. Александров А. С. Обобщающая модель пластического деформирования дискретных материалов дорожных конструкций при воздействии циклических нагрузок // Строительные материалы. 2016. № 5. С. 27–30.

16. Стригун Т. В., Александрова Н. П. Моделирование пластических деформаций дискретных материалов в слоях дорожных конструкций// В сборнике: Наука XXI века: опыт прошлого — взгляд в будущее: материала II международной научно-практической конференции — Омск, СибАДИ, 2016. — С. 229–233.

17. Александров А. С. Применение теории наследственной ползучести к расчету деформаций при воздействии повторных нагрузок: монография. — Омск: СибАДИ, 2014. — 152 с.

18. Александров А. С., Киселева Н. Ю. Пластическое деформирование гнейс- и диабаз материалов при воздействии повторяющихся нагрузок // Известия высших учебных заведений. Строительство. — 2012. — № 6. — С. 49–59.

19. Семенова Т. В., Гордеева С. А., Герцог В. Н. Определение пластических деформаций материалов, используемых в дорожных конструкциях // Вестник Томского государственного архитектурно-строительного университета. — 2012. — № 4 (37). — С. 247–254.

20. Семенова Т. В., Герцог В. Н. Пластическое деформирование материалов с дискретной структурой в условиях трехосного сжатия при воздействии циклических нагрузок // Вестник Сибирской государственной автомобильно-дорожной академии. — 2013. — № 1 (29). — С. 68–73.

21. Александров А. С. Пластическое деформирование гранодиоритового щебня и песчано-гравийной смеси при воздействии трехосной циклической нагрузки // Инженерно-строительный журнал. — 2013. — № 4 (39) — С. 22–34.

22. Кузин Н. В. Расчет пластических смещений асфальтобетонных порожных покрытий // Молодой ученый. — 2016. — № 10 (114). — С. 253–255.

23. Кузин Н. В. Исследование пластичности дорожных асфальтобетонов // Молодой ученый. — 2016. — № 10 (114). — С. 255–257.

24. Долгих Г. В. Расчет грунтов земляного полотна по критерию безопасных давлений // Вестник Сибирской государственной автомобильно-дорожной академии. — 2013. — № 6 (34). — С. 43–49.

25. Долгих Г. В. Применение критерия безопасных давлений для расчета дорожных конструкций по сопротивлению сдвигу в грунте земляного полотна // // В сборнике: Политранспортные системы материалы VIII Международной научно-технической конференции в рамках года науки Россия — ЕС. Новосибирск: СГУПС, 2015. — С. 176–182.

26. Александров А. С., Долгих Г. В., Калинин А. Л. О допускаемых давлениях на грунты земляного полотна и слои дорожной одежды // Наука и техника в дорожной отрасли. — 2012. № 2. — С. 10–13.

27. Чусов В. В. Перспективы применения эмпирических условий пластичности грунтов и определение их параметров при трехосных испытаниях грунтов Вестник ВолГАСУ. — 2015. № 42 (61). — С. 49–57.

28. Александров А. С., Долгих Г. В. Калинин А. Л. Модификация критериев прочности сплошной среды для расчета грунтов земляного полотна по сопротивлению сдвигу // В сборнике: Архитектура. Строительство. Транспорт. Технологии. Инновации Материалы Международного конгресса ФГБОУ ВПО «СибАДИ». — Омск: СибАДИ, 2013. — С. 228–235.

29. Александров А. С., Долгих Г. В., Калинин А. Л. Применение критерия Друкера — Прагера для модификации условий пластичности // Наука и техника в дорожной отрасли. — 2013. № 2. — С. 26–29.

30. Калинин А. Л. Совершенствование расчета касательных напряжений в дорожных конструкциях. Часть 1. Модификация критерия Писаренко-Лебедева и его применение при расчете касательных напряжений // Молодой ученый. — 2016. — № 6 (110). — С. 108–114.

31. Калинин А. Л. Применение модифицированных условий пластичности для расчета безопасных давлений на грунты земляного полотна. // Инженерно-строительный журнал — 2013. № 4 (39). — С. 35–45.

32. Александров А. С. Трехпараметрическое условие пластичности Кулона–Мора. Часть 1. Вывод критерия. // В сборнике: Наука XXI века: опыт прошлого — взгляд в будущее: материала II международной научно-практической конференции — Омск, СибАДИ, 2016. — С. 50–54.

33. Александров А. С. Трехпараметрическое условие пластичности Кулона–Мора. Часть 2. Круги предельных напряжений. // В сборнике: Наука XXI века: опыт прошлого — взгляд в будущее: материала II международной научно-практической конференции — Омск, СибАДИ, 2016. — С. 54–59.

34. Александров А. С. Трехпараметрическое условие пластичности Кулона–Мора. Часть 3. Определение параметров материала. // В сборнике: Наука XXI века: опыт прошлого — взгляд в будущее: материала II международной научно-практической конференции — Омск, СибАДИ, 2016. — С. 59–64.

35. Калинин А. Л. Способ модификации условий пластичности // В сборнике: Наука XXI века: опыт прошлого — взгляд в будущее: материала II международной научно-практической конференции — Омск, СибАДИ, 2016. — С. 59–150.

36. Александров А. С., Калинин А. Л. Совершенствование расчета дорожных конструкций по сопротивлению сдвигу. Часть 1. Учет деформаций в условии пластичности Кулона — Мора // Инженерно-строительный журнал. — 2015. № 7 (59). — С. 4–17.
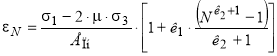
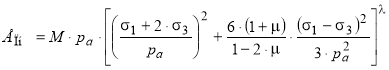
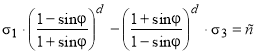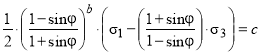