В данной работе приведен алгоритм построения стабилизирующего управления для системы дифференциальных уравнений с запаздыванием в управлении и найден критерий существования такого управления.
Ключевые слова: управление, запаздывание, дифференциальные уравнения с запаздыванием, устойчивость
Дифференциальные уравнения с запаздыванием в управлении возникают при решении различных экономических и технических задач. В данной работе рассматривается линейная система с запаздыванием в управлении. Основной целью работы является построение стабилизирующего управления и нахождение критериев его существования.
Задача построения стабилизирующего управления.
Рассмотрим линейную систему с запаздыванием в управлении:
(1)
где ℎ > 0 — запаздывание, матрицы
. Предположим также, что пара матриц 
— полностью управляема. Требуется выбрать управление таким образом, чтобы замкнутая система оказалась асимптотически устойчивой. В [1] было предложено выбирать управление в виде
В момент 
, когда определяется управление, значение 
ещё неизвестно. Из (1) получим, что
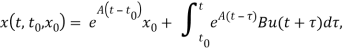
(2)
Построенное таким образом управление (2) является хорошим, поскольку зависит только от 
и от значений 
на интервале 
, т. е. не требует от нас знания будущих состояний системы.
Проверим, что замкнутая система (1)–(2) устойчива, то есть все корни её характеристического уравнения имеют отрицательные вещественные части. Для этого умножим
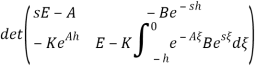
на
и в результате получим
В силу сделанного предположения о полной управляемости пары матриц найдётся стабилизирующее систему управление. Следует отметить, что выбранное управления обеспечивает конечный спектр замкнутой системы (1)–(2), несмотря на наличие запаздывания в системе (1).
Непосредственное использование управления (2) затруднено необходимостью вычисления интеграла
Продифференцировав данное соотношение, получим дифференциальное уравнение, решение которого позволяет находить 
Однако, как было замечено в [1], это приводит к появлению в системе дополнительного уравнения для 𝑧(𝑡), которое в отдельности является неустойчивым (если исходная система неустойчива). Более того, полученная таким образом система
оказывается неустойчивой даже для стабилизирующего управления. В самом деле, умножив характеристическую матрицу
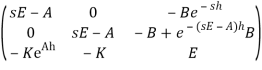
последовательно на
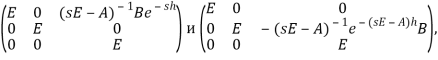
получим
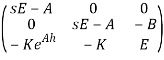
откуда характеристическая функция имеет вид
Поэтому, в [1] было рекомендовано аппроксимировать интеграл квадратурной формулой:
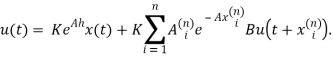(3)
Таким образом получим новую замкнутую систему (1)–(3). Можно проверить, что её спектр, в отличии от исходной системы, бесконечен. Для некоторых значениях параметров 
устойчивость системы (1)–(3) не достигается ни при каком количестве узлов 𝑛.
Поиск допустимых значений коэффициента ввыражении для стабилизирующего управления.
Далее для простоты расчетов будем рассматривать скалярный случай, то есть 
, 
, 
. Для устойчивости системы (1)–(2) необходимо, чтобы уравнение внутренней динамики управления:
(4)
оказалось устойчивым. Это означает, что уравнение
имеет только такие решения 
, что 
, где Re(s) -вещественная часть комплексного числа s. С учётом того, что
если
, то для устойчивости (4) достаточно, чтобы было выполнено следующее условие:
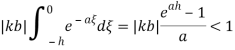
Учитывая вышесказанное, параметр 𝑘 управления (3) будем выбирать из следующих условий:
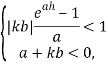
или, что то же самое,
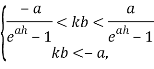
ввиду того, что 
для всех 𝑎. Так как
то получаем условие
Множество 
, удовлетворяющих условию, будет непусто, если
или, что то же самое,
Область, соответствующая допустим значениям 
, приведена на рис. 1.
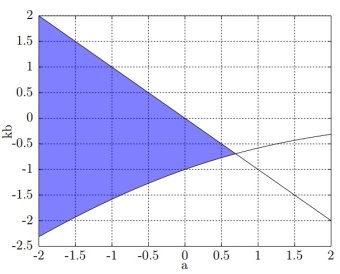
Рис. 1: Возможные значения kb для h=1
Заключение.
В данной работе предложен алгоритм построения стабилизирующего управления на основе метода компенсации запаздывания. Кроме того был найден критерий существования стабилизирующего управления для случая когда матричные коэффициенты являются скалярами. Очевидно, что для скалярного случая существование стабилизирующего управления не зависит от величины b.
Литература:
- Manitius A., Olbrot A. W. Finite spectrum assignment problem for systems with delays // Automatic Control, IEEE Transactions on, 1979. № 24(4). P. 541–552.
- Michiels W., S. Mondi´e, D. Roose. Finite Spectrum Assignment of Unstable Time-Delay Systems With a Safe Implementation// Automatic Control, IEEE Transactions on, 2003. № 12. P. 2207–2212
