Генерация крупномасштабных магнитных полей ивихревых структур во вращающейся электропроводящей самогравитирующей среде смелкомасштабной неспиральной силой
Копп Михаил Иосифович, кандидат физико-математических наук
В настоящей работе найдена новая крупномасштабная неустойчивость во вращающейся стратифицированной самогравитирующей электропроводящей среде с мелкомасштабной турбулентностью. Турбулентность возбуждается внешней мелкомасштабной силой с нулевой спиральностью и малым числом Рейнольдса. Теория построена на основе метода многомасштабных асимптотических разложений. В пятом порядке теории возмущений получены основные уравнения, описывающие неустойчивости типа гидродинамического и магнитогидродинамического α-эффектов во вращающейся турбулентной среде. Получены критерии возникновения двух α-эффектов при наличии мелкомасштабных пульсаций магнитного поля с нулевой спиральностью. Численные оценки характерных масштабов крупномасштабной неустойчивости приведены на примере галактической плазмы.
Ключевые слова: сила Кориолиса, многомасштабные асимптотические разложения, стратифицированная самогравитирующая электропроводящая среда, неспиральная мелкомасштабная турбулентность, α-эффект, спиральные галактики
In this paper we found a new large-scale instability in the rotating self-gravitating stratified electrically conductive medium to small-scale turbulence. Turbulence excited small-scale external force with zero helicity and low Reynolds number. The theory is based on the method of multi-scale asymptotic expansions. In the fifth-order perturbation theory, the basic equations that describe the type of hydrodynamic and magnetohydrodynamic α-effects in the rotating turbulent medium. Criteria for the occurrence of the two α-effects in the presence of small-scale magnetic field fluctuations with zero helicity are obtained. Numerical evaluation of the characteristic scales instability shown by the example of the galactic plasma.
Keywords: сoriolis force, multiscale asymptotic expansions, self-gravitating stratified conductive medium, nonspiral small-scale turbulence, α-effect, spiral galaxies
Открытое в работах [1–6] явление генерации крупномасштабных магнитных полей однородной изотропной, но зеркально-несимметричной (спиральной) турбулентностью получило название α-эффекта. На основе этого эффекта были построены различные теории, объясняющие происхождение магнитных полей у различных астрофизических объектов: планет и Солнца [1–5], галактик [6] и т. п. В последнем обзоре по этой теме [7] широко обсуждаются лабораторные динамо-эксперименты. Развитие вычислительной физики [7] также способствовало применению α-теорий к различным прикладным задачам, что в конечном счете привело к определению нового самостоятельного раздела физики — теории динамо. В современном понятии теория динамо включает в себя и так называемое вихревое динамо, которое описывает эффект генерации крупномасштабных вихрей в турбулентных средах [8]. Теория вихревого динамо началась с работы [9], где была высказана гипотеза о том, что спиральная турбулентность способна генерировать крупные вихри. Эта гипотеза основывалась на сходстве уравнений индукции магнитного поля ![]() и вихря
и вихря ![]() в гидродинамике. Однако в работе [10] было показано отсутствие эффекта генерации крупномасштабных вихрей однородной изотропной спиральной турбулентностью в несжимаемой жидкости. Причина отрицательного эффекта заключается в определенной симметрии тензора напряжений Рейнольдса в осредненном уравнении Навье-Стокса. Несмотря на запрет этой теоремы антидинамо, первый пример вихревого динамо в спиральной турбулентности для сжимаемой жидкости был найден в работе [11]. Там впервые было получено линеаризованное уравнение для вихря
в гидродинамике. Однако в работе [10] было показано отсутствие эффекта генерации крупномасштабных вихрей однородной изотропной спиральной турбулентностью в несжимаемой жидкости. Причина отрицательного эффекта заключается в определенной симметрии тензора напряжений Рейнольдса в осредненном уравнении Навье-Стокса. Несмотря на запрет этой теоремы антидинамо, первый пример вихревого динамо в спиральной турбулентности для сжимаемой жидкости был найден в работе [11]. Там впервые было получено линеаризованное уравнение для вихря ![]() , которое по виду похоже на уравнение индукции для среднего поля
, которое по виду похоже на уравнение индукции для среднего поля![]() . Эффект генерации крупномасштабных вихрей связан с появлением члена
. Эффект генерации крупномасштабных вихрей связан с появлением члена ![]() , где
, где ![]() выражается через спиральность турбулентности. Этот эффект получил название гидродинамического альфа-эффекта. Дальнейшее направление развития теории вихревого динамо было основано на поиске дополнительных факторов, нарушающих симметрию уравнений. Этими факторами, кроме сжимаемости среды, являются например, неоднородный поток [12], градиент температуры в поле тяжести [13], частицы примеси и пузырьки воздуха в жидкости [12]. На начальном этапе развития теории динамо, замкнутые уравнения для средних (крупномасштабных) полей были получены в основном при помощи метода электродинамики среднего поля (или теории корреляционного сглаживания второго порядка) [5] и функциональной техники [14, 15]. Оба эти метода в применении к задачам теории динамо имеют главный недостаток, заключающийся в трудности определения из всей иерархии возмущений главного порядка при котором возникает неустойчивость. В связи с этим, в работе [16] была рассмотрена крупномасштабная неустойчивость в несжимаемой жидкости методом асимптотических многомасштабных разложений. В качестве малого параметра для асимптотического метода многомасштабных разложений используется число Рейнольдса
выражается через спиральность турбулентности. Этот эффект получил название гидродинамического альфа-эффекта. Дальнейшее направление развития теории вихревого динамо было основано на поиске дополнительных факторов, нарушающих симметрию уравнений. Этими факторами, кроме сжимаемости среды, являются например, неоднородный поток [12], градиент температуры в поле тяжести [13], частицы примеси и пузырьки воздуха в жидкости [12]. На начальном этапе развития теории динамо, замкнутые уравнения для средних (крупномасштабных) полей были получены в основном при помощи метода электродинамики среднего поля (или теории корреляционного сглаживания второго порядка) [5] и функциональной техники [14, 15]. Оба эти метода в применении к задачам теории динамо имеют главный недостаток, заключающийся в трудности определения из всей иерархии возмущений главного порядка при котором возникает неустойчивость. В связи с этим, в работе [16] была рассмотрена крупномасштабная неустойчивость в несжимаемой жидкости методом асимптотических многомасштабных разложений. В качестве малого параметра для асимптотического метода многомасштабных разложений используется число Рейнольдса ![]() для мелкомасштабных пульсаций скорости
для мелкомасштабных пульсаций скорости ![]() , вызванных мелкомасштабной силой. Модель внешней мелкомасштабной силы была выбрана с нарушением четности (при нулевой спиральности). Эффект генерации крупномасштабных возмущений такой силой получил название анизотропного кинетического альфа-эффекта или АКА-эффекта [16]. Отметим, что нарушение четности является наиболее общим понятием, чем спиральность, хотя именно спиральность
, вызванных мелкомасштабной силой. Модель внешней мелкомасштабной силы была выбрана с нарушением четности (при нулевой спиральности). Эффект генерации крупномасштабных возмущений такой силой получил название анизотропного кинетического альфа-эффекта или АКА-эффекта [16]. Отметим, что нарушение четности является наиболее общим понятием, чем спиральность, хотя именно спиральность ![]() является самым распространенным механизмом нарушения четности гидродинамических течений. В дальнейшем, применяя метод многомасштабных асимптотических разложений были разработаны линейные и нелинейные теории вихревого динамо для сжимаемых сред [17, 18], конвективных сред со спиральной внешней силой [19–21], для сред с учетом эффектов вращения [22–25]. В упомянутых выше работах спиральная турбулентность считалась заданной. Генерацию спиральной турбулентности в природных условиях обычно связывают с влиянием силы Кориолиса (или силы Лоренца) на турбулентное движение среды [1, 26], которое изначально было однородным изотропным и зеркально-симметричным (неспиральным). В связи с этим возникает вопрос о возможности генерации крупномасштабных полей (вихревых и магнитных) во вращающихся средах под действием мелкомасштабной силы с нулевой спиральностью:
является самым распространенным механизмом нарушения четности гидродинамических течений. В дальнейшем, применяя метод многомасштабных асимптотических разложений были разработаны линейные и нелинейные теории вихревого динамо для сжимаемых сред [17, 18], конвективных сред со спиральной внешней силой [19–21], для сред с учетом эффектов вращения [22–25]. В упомянутых выше работах спиральная турбулентность считалась заданной. Генерацию спиральной турбулентности в природных условиях обычно связывают с влиянием силы Кориолиса (или силы Лоренца) на турбулентное движение среды [1, 26], которое изначально было однородным изотропным и зеркально-симметричным (неспиральным). В связи с этим возникает вопрос о возможности генерации крупномасштабных полей (вихревых и магнитных) во вращающихся средах под действием мелкомасштабной силы с нулевой спиральностью: ![]() .
.
Используя метод многих масштабов, в настоящей работе рассмотрена генерация крупномасштабных полей (магнитных и вихревых) в стратифицированной вращающейся электропроводящей среде с учетом ее самогравитации. Данная работа является обобщением работы [25] на случай электропроводящей среды. Полученные здесь инкременты неустойчивости соответствуют гидродинамическому и магнитогидродинамическому альфа-эффектам, которые возникают в результате совместного действия неспиральной силы, вращения и стратификации среды. Рассмотрено также влияние мелкомасштабных магнитных флуктуаций ![]() с нулевой спиральностью
с нулевой спиральностью ![]() на генерацию крупномасштабных вихревых и магнитных полей. Результаты настоящей работы могут найти применение к ряду астрофизических задач.
на генерацию крупномасштабных вихревых и магнитных полей. Результаты настоящей работы могут найти применение к ряду астрофизических задач.
Основные уравнения ипостановка задачи.
Динамику вращающейся электропроводящей среды (плазмы) с учетом ее самогравитации описываем хорошо известными уравнениями магнитной гидродинамики:
![]() (2)
(2)
![]() (3)
(3)
![]()
![]() (4)
(4)
Здесь ![]() ,
, ![]() , P,
, P, ![]() ,
,![]() — возмущения скорости, плотности, давления, индукции магнитного поля и гравитационного потенциала среды относительно равновесного состояния:
— возмущения скорости, плотности, давления, индукции магнитного поля и гравитационного потенциала среды относительно равновесного состояния:
![]() (5)
(5)
где ![]() – радиус-вектор элемента среды. Коэффициенты
– радиус-вектор элемента среды. Коэффициенты ![]() и
и ![]() соответствуют первой и второй кинематической вязкости для сжимаемой среды,
соответствуют первой и второй кинематической вязкости для сжимаемой среды, ![]() — коэффициенты динамической вязкости,
— коэффициенты динамической вязкости, ![]() — коэффициент магнитной вязкости,
— коэффициент магнитной вязкости, ![]() – коэффициент электропроводности среды,
– коэффициент электропроводности среды, ![]() - гравитационная постоянная. С целью упрощения вычислений выберем декартовую геометрию задачи, для которой вектор угловой скорости
- гравитационная постоянная. С целью упрощения вычислений выберем декартовую геометрию задачи, для которой вектор угловой скорости ![]() считаем постоянным и направленным вдоль оси
считаем постоянным и направленным вдоль оси ![]() вертикально вверх (
вертикально вверх (![]() -единичный вектор по вертикали). Уравнения (1)-(4) дополним уравнением состояния среды, которое для простоты выберем в виде:
-единичный вектор по вертикали). Уравнения (1)-(4) дополним уравнением состояния среды, которое для простоты выберем в виде:
![]() (6)
(6)
Здесь ![]() – скорость звука. Уравнение равновесия (5), используя (6), перепишем в следующем виде:
– скорость звука. Уравнение равновесия (5), используя (6), перепишем в следующем виде:
![]() (7)
(7)
Здесь ![]() ,
, ![]() , где
, где ![]() =
=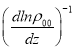 - характерный масштаб неоднородности или стратификации среды, которая возникает естественным образом в поле гравитации. Выбор обозначений для равновесного состояния (индекс с двумя нулями) связан с избежанием путаницы при использовании обозначений асимптотических разложений далее. В уравнение (1) включена внешняя сила
- характерный масштаб неоднородности или стратификации среды, которая возникает естественным образом в поле гравитации. Выбор обозначений для равновесного состояния (индекс с двумя нулями) связан с избежанием путаницы при использовании обозначений асимптотических разложений далее. В уравнение (1) включена внешняя сила ![]() , моделирующая источник возбуждения в среде мелкомасштабных и высокочастотных флуктуаций поля скорости
, моделирующая источник возбуждения в среде мелкомасштабных и высокочастотных флуктуаций поля скорости ![]() с малым числом Рейнольдса
с малым числом Рейнольдса ![]() . Рассмотрим неспиральную внешнюю силу
. Рассмотрим неспиральную внешнюю силу ![]() со следующими свойствами:
со следующими свойствами:
div
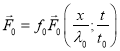 (9)
(9)
где ![]() – характерный масштаб,
– характерный масштаб, ![]() - характерное время,
- характерное время, ![]() - характерная амплитуда. Заметим, что мелкомасштабное магнитное поле
- характерная амплитуда. Заметим, что мелкомасштабное магнитное поле ![]() в линейном приближении не может возбуждаться внешней мелкомасштабной силой
в линейном приближении не может возбуждаться внешней мелкомасштабной силой ![]() , так как это следует из уравнения (3). Поэтому ниже мы рассмотрим два возможных сценария развития крупномасштабной неустойчивости. Первый, когда мелкомасштабное магнитное поле
, так как это следует из уравнения (3). Поэтому ниже мы рассмотрим два возможных сценария развития крупномасштабной неустойчивости. Первый, когда мелкомасштабное магнитное поле ![]() существует изначально, и второй, когда мелкомасштабное поле
существует изначально, и второй, когда мелкомасштабное поле ![]() создается внешним источником
создается внешним источником ![]() , имеющим такие же топологические свойства как и сила
, имеющим такие же топологические свойства как и сила ![]() , т. е.
, т. е. ![]() . Естественно, что возбуждаемое таким источником магнитное поле также неспирально:
. Естественно, что возбуждаемое таким источником магнитное поле также неспирально: ![]() . Характерный масштаб источника
. Характерный масштаб источника ![]() и характерное время
и характерное время ![]() удобно выбрать совпадающими с характерными масштабами
удобно выбрать совпадающими с характерными масштабами ![]() и
и ![]() соответственно, но характерные амплитуды этих источников будем предполагать разными:
соответственно, но характерные амплитуды этих источников будем предполагать разными:
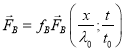 ,
, ![]() .
.
Кроме того, среду для простоты будем считать безграничной и пренебрежем влиянием внешнего магнитного поля. В такой постановке проблема представляет интерес для теории динамо [2–6]. Теперь перейдем в уравнениях (1)-(4) к безразмерным переменным:
![]()
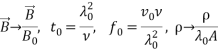 ,
, ![]() ,
, ![]() ,
, ![]()
В безразмерных переменных уравнения (1)-(4) примут вид:
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
![]()
![]() (13)
(13)
где
![]() ,
, ![]() (14)
(14)
где ![]() и
и ![]() – обозначают производные по быстрым переменным
– обозначают производные по быстрым переменным ![]() , а
, а ![]() и
и ![]() – производные по медленным переменным
– производные по медленным переменным ![]() . Переменные
. Переменные ![]() и
и ![]() соответственно можно назвать мелкомасштабные и крупномасштабные переменные. Для переменных
соответственно можно назвать мелкомасштабные и крупномасштабные переменные. Для переменных ![]() ,
, ![]() ,
, ![]() ,
,![]() представим разложение в виде ряда по малому параметру R:
представим разложение в виде ряда по малому параметру R:
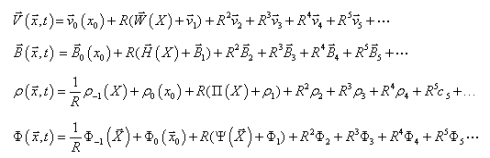 (15)
(15)
Подставляя разложения (14)-(15) в систему уравнений (10)-(13) и собирая вместе члены с одинаковыми порядками по ![]() до степени
до степени ![]() включительно, получим уравнения многомасштабного асимптотического разложения. В пятом порядке по
включительно, получим уравнения многомасштабного асимптотического разложения. В пятом порядке по ![]() теории возмущений получим основную систему секулярных уравнений для описания эволюции крупномасштабных возмущений:
теории возмущений получим основную систему секулярных уравнений для описания эволюции крупномасштабных возмущений:
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
Эти уравнения дополним секулярными уравнениями, полученными в других порядках по ![]() :
:
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() (20)
(20)
Из уравнений (20) следует, что для крупномасштабных двумерных движений устанавливается баланс сил Кориолиса и гравитации. Двумерность поля скорости ![]() позволяет рассматривать уравнения (16)-(19) в рамках квазидвумерной задачи, когда крупномасштабные производные по Z предпочтительнее, т. е.
позволяет рассматривать уравнения (16)-(19) в рамках квазидвумерной задачи, когда крупномасштабные производные по Z предпочтительнее, т. е. ![]() а крупномасштабные возмущения
а крупномасштабные возмущения ![]() зависят только от
зависят только от ![]() - координаты:
- координаты:
![]() (22)
(22)
На начальном этапе эволюцию крупномасштабных возмущений можно представить в виде плоской волны с волновым вектором ![]() . Тогда из условия соленоидальности крупномасштабного магнитного поля:
. Тогда из условия соленоидальности крупномасштабного магнитного поля: ![]() или
или ![]() ясно, что поле
ясно, что поле ![]() имеет компоненты
имеет компоненты ![]() Для исследования устойчивости малых крупномасштабных возмущений в уравнениях (16)-(19) можно пренебречь нелинейными членами. В итоге упрощенная система уравнений, описывающая эволюцию крупномасштабных возмущений, принимает вид:
Для исследования устойчивости малых крупномасштабных возмущений в уравнениях (16)-(19) можно пренебречь нелинейными членами. В итоге упрощенная система уравнений, описывающая эволюцию крупномасштабных возмущений, принимает вид:
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
![]() (26)
(26)
![]() (27)
(27)
![]() (28)
(28)
![]() =0(29)
=0(29)
Поскольку исследуется проблема генерации крупномасштабных вихревых движений и магнитных полей во вращающейся электропроводящей среде с мелкомасштабными и высокочастотными флуктуациями, то достаточно получить уравнения (23)-(26) в замкнутом виде. Для этой цели нужно вычислить корреляторы:
![]()
![]() (30)
(30)
![]()
![]() (31)
(31)
![]() ,
, ![]() (32)
(32)
![]() ,
, ![]() (33)
(33)
Их вычисление осуществляется используя решения уравнений для мелкомасштабных полей в нулевом и во втором порядках по ![]() .
.
Замкнутые уравнения для крупномасштабных полей.
В целях упрощения расчетов, выберем неспиральную внешнюю силу ![]() , удовлетворяющую условиям (10), в следующем виде:
, удовлетворяющую условиям (10), в следующем виде:
![]() (34)
(34)
где ![]() – амплитуда внешней силы,
– амплитуда внешней силы, ![]() ,
, ![]() ,
, ![]() . Вид внешней силы
. Вид внешней силы ![]() (34) можно записать в комплексной форме:
(34) можно записать в комплексной форме:
![]() (35)
(35)
которая и будет использоваться в дальнейших вычислениях. Мелкомасштабное магнитное поле
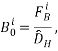 (36)
(36)
где введено обозначение для оператора ![]() . Отсюда видно, что топологические свойства мелкомасштабного поля будут заданы самим источником
. Отсюда видно, что топологические свойства мелкомасштабного поля будут заданы самим источником ![]() .
.
Для неспирального внешнего источника ![]() его вид можно аппроксимировать следующей формулой:
его вид можно аппроксимировать следующей формулой:
![]()
или в комплексной форме:
![]() (37)
(37)
Отличие вида внешней неспиральной силы ![]() и источника
и источника ![]() состоит в разных по величине безразмерных амплитудах:
состоит в разных по величине безразмерных амплитудах: ![]() . Используя приведенные выше соотношения (35), (37) и выражения для мелкомасштабных полей в нулевом и во втором порядках по
. Используя приведенные выше соотношения (35), (37) и выражения для мелкомасштабных полей в нулевом и во втором порядках по ![]() получим замкнутую систему уравнений, которая описывает эволюцию крупномасштабных полей скорости
получим замкнутую систему уравнений, которая описывает эволюцию крупномасштабных полей скорости ![]() и магнитной индукции
и магнитной индукции ![]() :
:
![]() (38)
(38)
![]() (39)
(39)
![]() (40)
(40)
Из уравнений (38)-(41) видно, что коэффициенты ![]() и
и ![]() отвечают за конвективный перенос крупномасштабных возмущений скорости
отвечают за конвективный перенос крупномасштабных возмущений скорости ![]() и магнитного поля
и магнитного поля ![]() соответственно. Коэффициенты
соответственно. Коэффициенты ![]() и
и ![]() соответствуют гидродинамическому и МГД
соответствуют гидродинамическому и МГД ![]() - эффектам с помощью которых происходит генерация вихревых и магнитных возмущений. Посредством коэффициентов
- эффектам с помощью которых происходит генерация вихревых и магнитных возмущений. Посредством коэффициентов ![]() ,
, ![]() ,
, ![]() осуществляется взаимное влияние крупномасштабного поля скорости
осуществляется взаимное влияние крупномасштабного поля скорости ![]() на динамику магнитного поля
на динамику магнитного поля ![]() и наоборот. Если предположить отсутствие источника мелкомасштабных магнитных полей (
и наоборот. Если предположить отсутствие источника мелкомасштабных магнитных полей (![]() , то система самосогласованных уравнений (38)-(41) расщепляется на две пары не связанных уравнений для крупномасштабной скорости
, то система самосогласованных уравнений (38)-(41) расщепляется на две пары не связанных уравнений для крупномасштабной скорости ![]() :
:
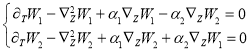 (42)
(42)
и крупномасштабного магнитного поля ![]() :
:
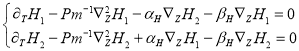 (43)
(43)
Первая система уравнений (42), за исключением конвективных членов, соответствует уравнениям гидродинамического ![]() - эффекта [8], который приводит к генерации крупномасштабных вихревых структур. Вторая система уравнений (43), также за исключением конвективных членов, описывает хорошо известный из теории динамо [1–7] МГД
- эффекта [8], который приводит к генерации крупномасштабных вихревых структур. Вторая система уравнений (43), также за исключением конвективных членов, описывает хорошо известный из теории динамо [1–7] МГД ![]() - эффект, приводящий к генерации крупномасштабного магнитного поля мелкомасштабной спиральной турбулентностью. Ниже рассмотрим генерацию крупномасштабных возмущений в более общем случае, который соответствует системе уравнений (38)-(41).
- эффект, приводящий к генерации крупномасштабного магнитного поля мелкомасштабной спиральной турбулентностью. Ниже рассмотрим генерацию крупномасштабных возмущений в более общем случае, который соответствует системе уравнений (38)-(41).
Крупномасштабная неустойчивость.
Приступим сначала к анализу возможности появления крупномасштабной неустойчивости в системе уравнений (42)-(43). Для этого выберем крупномасштабные возмущения скорости ![]() и магнитной индукции
и магнитной индукции ![]() в виде плоских волн с волновым вектором
в виде плоских волн с волновым вектором ![]() :
:
![]() (44)
(44)
![]() ,
,
где ![]() ,
, ![]() — амплитуды волновых возмущений.
— амплитуды волновых возмущений.
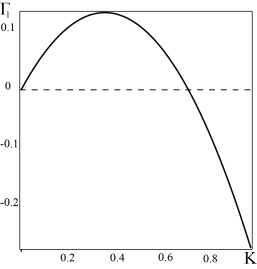
Рис. 1. График зависимости инкремента неустойчивости ![]() от волновых
от волновых
чисел ![]()
Подставляя (44) в систему уравнений (42)-(43) получим дисперсионные уравнения для случая отсутствия источника мелкомасштабных магнитных полей (![]() :
:
![]()
![]() (45)
(45)
Решения уравнений (45) содержат как реальную, так и мнимую часть частоты ![]() :
:
![]()
![]() (46)
(46)
![]()
![]()
Как видно из (46), крупномасштабные возмущения могут не только нарастать (затухать) со временем, но и совершать колебания с частотами ![]() и
и ![]() . Коэффициенты
. Коэффициенты ![]() и
и ![]() имеют смысл фазовой (групповой) скорости распространения вихревых и магнитных возмущений соответственно. В наиболее интересном физическом случае
имеют смысл фазовой (групповой) скорости распространения вихревых и магнитных возмущений соответственно. В наиболее интересном физическом случае ![]() и при
и при ![]() эти коэффициенты
эти коэффициенты ![]() и
и ![]() принимают самый простой вид:
принимают самый простой вид:
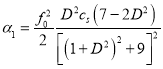 (47)
(47)
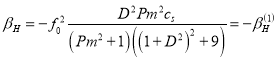 (48)
(48)
Решение с первым инкрементом ![]() (см. Рис. 1) описывает генерацию крупномасштабных вихревых структур во вращающейся стратифицированной электропроводящей среде с коэффициентом усиления
(см. Рис. 1) описывает генерацию крупномасштабных вихревых структур во вращающейся стратифицированной электропроводящей среде с коэффициентом усиления ![]() равным:
равным:
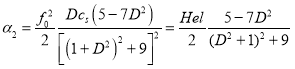 (49)
(49)
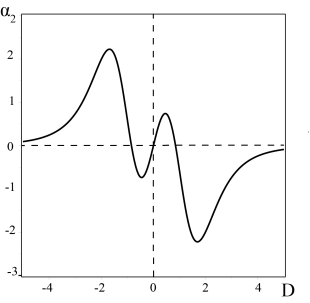
Рис. 2. График зависимости ГД ![]() -эффекта от вращения среды (параметра
-эффекта от вращения среды (параметра ![]() ) при
) при ![]() и
и ![]()
Величина коэффициента ![]() зависит от параметра вращения среды
зависит от параметра вращения среды ![]() , график зависимости которой изображен на Рис. 2. При увеличении эффекта вращения (
, график зависимости которой изображен на Рис. 2. При увеличении эффекта вращения (![]() ) мы наблюдаем стремление
) мы наблюдаем стремление ![]() , или подавление ГД
, или подавление ГД ![]() - эффекта. Подобное явление было описано в работе [32]. Антисимметричная зависимость
- эффекта. Подобное явление было описано в работе [32]. Антисимметричная зависимость ![]() от параметра вращения
от параметра вращения ![]() позволяет перенести сделанные выше выводы для области отрицательных значений проекций
позволяет перенести сделанные выше выводы для области отрицательных значений проекций ![]() в обратном порядке. Инкремент вихревой неустойчивости (
в обратном порядке. Инкремент вихревой неустойчивости (![]() ) имеет вид известного из линейной теории динамо
) имеет вид известного из линейной теории динамо ![]() - эффекта (см. Рис. 1). Максимальное значение инкремент неустойчивости
- эффекта (см. Рис. 1). Максимальное значение инкремент неустойчивости ![]() достигает при
достигает при ![]() .
.
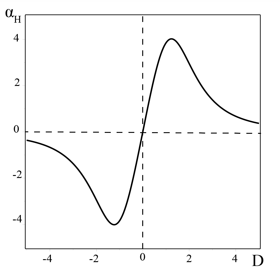
Рис. 3. График зависимости МГД ![]() -эффекта от вращения жидкости (параметра
-эффекта от вращения жидкости (параметра ![]() ) для магнитных чисел Прандтля
) для магнитных чисел Прандтля ![]() при при
при при ![]() и
и ![]()
Магнитогидродинамический ![]() -эффект (или
-эффект (или ![]() -эффект) также увеличивается при «медленном» вращении до максимального значения
-эффект) также увеличивается при «медленном» вращении до максимального значения 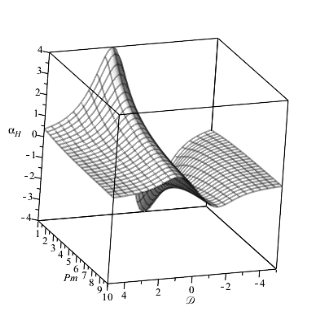
Рис. 4. Трехмерное изображение зависимости коэффициента ![]() от параметра вращения
от параметра вращения ![]() и числа Прандтля
и числа Прандтля ![]()
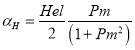 (50)
(50)
Максимальный инкремент ![]() достигает своего значения при волновых числах
достигает своего значения при волновых числах ![]() (см. Рис. 5). Эффект генерации крупномасштабного магнитного поля мелкомасштабной спиральной турбулентностью в электропроводящих средах хорошо известен (см. например [1–7]) и носит название магнитогидродинамического (МГД)
(см. Рис. 5). Эффект генерации крупномасштабного магнитного поля мелкомасштабной спиральной турбулентностью в электропроводящих средах хорошо известен (см. например [1–7]) и носит название магнитогидродинамического (МГД) ![]() -эффекта или
-эффекта или ![]() -эффекта. Полученные нами соотношения (49)-(50) указывают на существование двух
-эффекта. Полученные нами соотношения (49)-(50) указывают на существование двух ![]() -эффектов в электропроводящей среде с ненулевой спиральностью
-эффектов в электропроводящей среде с ненулевой спиральностью ![]() [25].
[25].
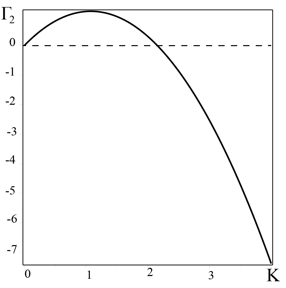
Рис. 5. График зависимости инкремента неустойчивости ![]() от волновых чисел
от волновых чисел ![]()
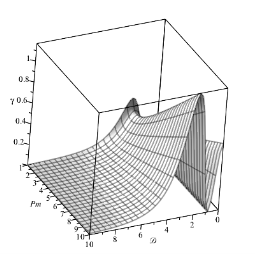
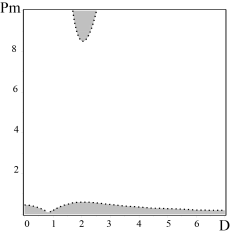
Рис. 6. Слева — трехмерное изображение зависимости коэффициента ![]() от параметра вращения
от параметра вращения ![]() и магнитного числа Прандтля
и магнитного числа Прандтля ![]() , справа — на рисунке показаны области
, справа — на рисунке показаны области ![]() (светлая часть) и
(светлая часть) и ![]() (темная часть) на плоскости
(темная часть) на плоскости ![]()
Для слабопроводящих сред (![]() )
) ![]() -эффект мал, поэтому происходит генерация только крупномасштабных вихревых движений. Эта закономерность особенно видна на Рис. 6, где изображена зависимость отношения
-эффект мал, поэтому происходит генерация только крупномасштабных вихревых движений. Эта закономерность особенно видна на Рис. 6, где изображена зависимость отношения ![]() от параметров вращения
от параметров вращения ![]() и магнитного числа Прандтля
и магнитного числа Прандтля ![]() :
:
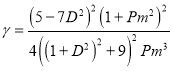 (51)
(51)
В правой части Рис. 6 на плоскости ![]() показаны области превосходства максимального инкремента неустойчивости для вихревых возмущений
показаны области превосходства максимального инкремента неустойчивости для вихревых возмущений ![]() над масксимальным инкрементом неустойчивости для магнитных возмущений
над масксимальным инкрементом неустойчивости для магнитных возмущений ![]() (
(![]() ) и наоборот (
) и наоборот (![]() ). На этом графике мы видим, что наибольшей области соответствует случай
). На этом графике мы видим, что наибольшей области соответствует случай ![]() , т. е. темпы роста магнитных возмущений выше чем вихревых возмущений. При фиксированных параметрах вращения
, т. е. темпы роста магнитных возмущений выше чем вихревых возмущений. При фиксированных параметрах вращения ![]() и магнитных числах Прандтля
и магнитных числах Прандтля ![]() из Рис. 5 видно, что
из Рис. 5 видно, что ![]() на интервале волновых чиисел
на интервале волновых чиисел ![]() . Таким образом, в результате развития крупномасштабной неустойчивости рост магнитных возмущений опережает рост вихревых возмущений.
. Таким образом, в результате развития крупномасштабной неустойчивости рост магнитных возмущений опережает рост вихревых возмущений.
Перейдем теперь к общему случаю при наличии мелкомасштабных стационарных флуктуаций магнитных полей, уровень которых поддерживается источником мелкомасштабной МГД-турбулентности. Раcсмотренный нами ![]() -эффект на линейной стадии возможен при наличии мелкомасштабного поля
-эффект на линейной стадии возможен при наличии мелкомасштабного поля ![]() , или так называемого в литературе [3] «затравочного» магнитного поля. В теории динамо, к настоящему времени, известно множество механизмов генерации «затравочных» магнитных полей, например, при термоэффекте [28], при развитии плазменных неустойчивостей [29–31] и т. д. Механизм возбуждения «затравочных» магнитных полей будем моделировать в виде внешнего источника, в результате действия которого возникают поля
, или так называемого в литературе [3] «затравочного» магнитного поля. В теории динамо, к настоящему времени, известно множество механизмов генерации «затравочных» магнитных полей, например, при термоэффекте [28], при развитии плазменных неустойчивостей [29–31] и т. д. Механизм возбуждения «затравочных» магнитных полей будем моделировать в виде внешнего источника, в результате действия которого возникают поля ![]() со спиральностью равной нулю:
со спиральностью равной нулю: ![]() . Динамика крупномасштабных полей в этих условиях описывается самосогласованной системой уравнений (38)-(41), в которой видно взаимное влияние крупномасштабного магнитного поля на вихревое движение среды и наоборот. С учетом источника флуктуаций магнитного поля общее решение системы уравнений (38)-(41) можно представить в следующем виде:
. Динамика крупномасштабных полей в этих условиях описывается самосогласованной системой уравнений (38)-(41), в которой видно взаимное влияние крупномасштабного магнитного поля на вихревое движение среды и наоборот. С учетом источника флуктуаций магнитного поля общее решение системы уравнений (38)-(41) можно представить в следующем виде:
В формуле (52) частота ![]() с учетом внешнего источника
с учетом внешнего источника ![]() имеет вид:
имеет вид:
![]() (53)
(53)
где ![]() ,
, ![]() .
.
Величина ![]() играет роль коэффициента усиления вихревых и магнитных возмущений, обусловленного действием внешнего источника
играет роль коэффициента усиления вихревых и магнитных возмущений, обусловленного действием внешнего источника![]() . Очевидно, что при
. Очевидно, что при ![]() решения (52) переходят в (44). Подставим решения (52) в систему уравнений (38)-(41), и проводя обычные вычисления, получим систему уравнений для амплитуд возмущений:
решения (52) переходят в (44). Подставим решения (52) в систему уравнений (38)-(41), и проводя обычные вычисления, получим систему уравнений для амплитуд возмущений:
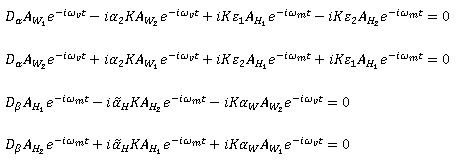 (54)
(54)
Условием разрешимости для системы уравнений (54) является равенство нулю детерминанта, после раскрытия которого получим дисперсионное уравнение:
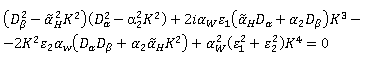 (55)
(55)
где введены следующие обозначения:
![]() (56)
(56)
Входящие в формулы (54)-(56) новые коэффициенты ![]() появляются в результате действия внешнего источника МГД турбулентности (
появляются в результате действия внешнего источника МГД турбулентности (![]() ), и при выполнении условия
), и при выполнении условия![]() и
и![]() они имеют следующий вид:
они имеют следующий вид:
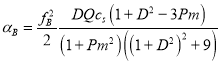 (57)
(57)
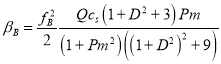 (58)
(58)
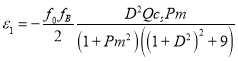 (59)
(59)
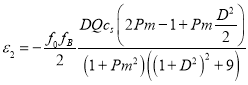 (60)
(60)
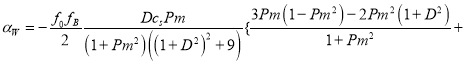
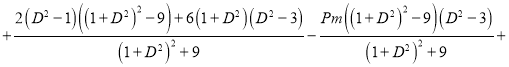
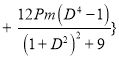 (61)
(61)
Дисперсионное уравнение (55), после несложных алгебраических преобразований, можно записать в другом более удобном виде:
![]() (62)
(62)
Извлекая квадратный корень с обеих сторон уравнения (62), оно распадается на два уравнения:
![]() (63)
(63)
Рассмотрим уравнение (63), которое после умножения левой и правой частей на ![]() сводится к уравнению для
сводится к уравнению для ![]() :
:
![]() (65)
(65)
Из (65) видно, что коэффициент ![]() комплексная величина и может быть представлен как
комплексная величина и может быть представлен как
![]() (66)
(66)
где ![]() – действительная часть
– действительная часть ![]() :
: ![]() – дает вклад в инкремент крупномасштабной неустойчивости,
– дает вклад в инкремент крупномасштабной неустойчивости, ![]() – мнимая часть
– мнимая часть ![]() дает вклад в частоту колебаний крупномасштабных возмущений. Подставляя (66) в (65) получим систему уравнений для
дает вклад в частоту колебаний крупномасштабных возмущений. Подставляя (66) в (65) получим систему уравнений для ![]() и
и ![]() :
:
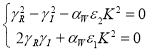 (67)
(67)
Отсюда легко найти значения ![]() и
и ![]() :
:
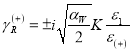 ,
, 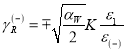 ,
, ![]() ,
, ![]() (68)
(68)
Здесь введены обозначения: ![]() ,
, ![]() .
.
Используя определение (66) находим общие выражения для коэффициента ![]() :
:
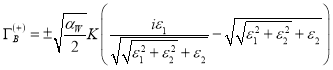 (69)
(69)
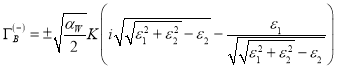 (70)
(70)
Согласно формуле (69) положительная часть ![]() дает вклад в инкремент крупномасштабной неустойчивости:
дает вклад в инкремент крупномасштабной неустойчивости:
![]() (71)
(71)
а мнимая часть ![]() дополнительную поправку к частоте колебаний:
дополнительную поправку к частоте колебаний:
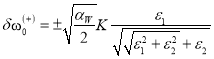 (72)
(72)
Аналогично находятся вклады в инкремент и частоту колебаний из решения (70):
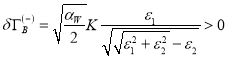 (73)
(73)
![]() (74)
(74)
Таким образом, учет источника мелкомасштабного магнитного поля приводит к перенормировке коэффициентов усиления и частот колебаний для ГД и МГД ![]() - эффектов:
- эффектов:
![]()
![]() (75)
(75)
где ![]() ,
, 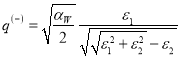
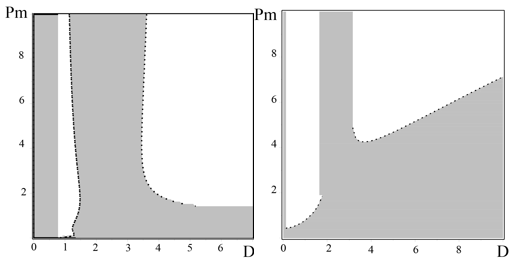
Рис. 7. Слева – светлая часть рисунка соответствует области неустойчивости вихревых возмущений, асправа – темная часть рисунка соответствует области неустойчивости магнитных возмущений при включенном источнике турбулентности ![]() ипараметрах
ипараметрах ![]() ,
, ![]()
Максимальные значения инкрементов соответственно принимают вид:
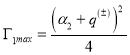 при
при ![]() (77)
(77)
![]() при
при ![]() (78)
(78)
Нетрудно заметить, что в полученные здесь добавки ![]() входят коэффициенты
входят коэффициенты ![]() посредством которых осуществляется влияние вихревых движений на магнитные поля и наоборот. Включение источника мелкомасштабного магнитного поля
посредством которых осуществляется влияние вихревых движений на магнитные поля и наоборот. Включение источника мелкомасштабного магнитного поля ![]() , как видно из выражений (77)-(78), приводит к перестройке порога неустойчивости. При помощи численных методов мы можем определить области неустойчивости для вихревых и магнитных возмущений. Для вихревых возмущений эта область изображена на Рис. 7 в плоскости
, как видно из выражений (77)-(78), приводит к перестройке порога неустойчивости. При помощи численных методов мы можем определить области неустойчивости для вихревых и магнитных возмущений. Для вихревых возмущений эта область изображена на Рис. 7 в плоскости ![]() для фиксированных значений
для фиксированных значений ![]() ,
, ![]() и амплитуд безразмерных внешних источников равных десяти:
и амплитуд безразмерных внешних источников равных десяти: ![]() . Аналогичным образом определяются области неустойчивости для магнитных возмущений, которые изображены также на Рис.7.
. Аналогичным образом определяются области неустойчивости для магнитных возмущений, которые изображены также на Рис.7.
Заключение.
В заключении приведем количественные оценки характерных масштабов и времен крупномасштабной неустойчивости на примере галактической среды. Начнем анализ оценок масштабов для неустойчивости типа гидродинамического ![]() -эффекта. Выше мы получили максимальное значение для инкремента неустойчивости вихревых возмущений
-эффекта. Выше мы получили максимальное значение для инкремента неустойчивости вихревых возмущений ![]() и соответственно – характерный масштаб неустойчивой моды
и соответственно – характерный масштаб неустойчивой моды ![]() и характерный временной масштаб ее нарастания
и характерный временной масштаб ее нарастания ![]() . Очевидно, что для нахождения этих масштабов нужно оценить коэффициент
. Очевидно, что для нахождения этих масштабов нужно оценить коэффициент ![]() . Из теории динамо [1–7] известно определение гидродинамической спиральности
. Из теории динамо [1–7] известно определение гидродинамической спиральности ![]() , которую выразим через безразмерную амплитуду источника:
, которую выразим через безразмерную амплитуду источника:
здесь ![]() — безразмерная амплитуда силы, входящая в формулы (49)-(50). При выводе этой формулы мы полагали установление баланса между источником и диссипацией в стационарном случае. Далее из формулы (49) коэффициент усиления
— безразмерная амплитуда силы, входящая в формулы (49)-(50). При выводе этой формулы мы полагали установление баланса между источником и диссипацией в стационарном случае. Далее из формулы (49) коэффициент усиления ![]() при малых числах параметра вращения
при малых числах параметра вращения ![]() (для центральной части нашей Галактики
(для центральной части нашей Галактики ![]() ) принимает вид:
) принимает вид:
![]()
Для оценок часто полагают ![]() (см. например [6]), и в итоге характерные пространственный и временной масштабы соответственно равны:
(см. например [6]), и в итоге характерные пространственный и временной масштабы соответственно равны:
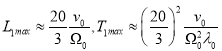
Используя эспериментальные данные для нашей Галактики: ![]() (центральная часть Галактики),
(центральная часть Галактики), ![]() ,
, ![]() (
(![]() ),
), ![]() [6] легко найти численные оценки
[6] легко найти численные оценки ![]() и
и ![]() :
: ![]() ,
,![]() . Это вполне приемлемые оценки характерных масштабов для галактической генерации крупномасштабной вихревой структуры спирального типа. Проводя аналогичные рассуждения можно вычислить характерные пространственные
. Это вполне приемлемые оценки характерных масштабов для галактической генерации крупномасштабной вихревой структуры спирального типа. Проводя аналогичные рассуждения можно вычислить характерные пространственные ![]() и временные масштабы
и временные масштабы ![]() для крупномасштабной неустойчивости МГД
для крупномасштабной неустойчивости МГД ![]() -эффекта:
-эффекта:
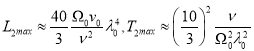
Численные оценки ![]() и
и ![]() показывают, что в галактической среде, в результате развития данной неустойчивости, крупномасштабное магнитное поле генерируется быстрее
показывают, что в галактической среде, в результате развития данной неустойчивости, крупномасштабное магнитное поле генерируется быстрее ![]() и имеет меньший характерный масштаб
и имеет меньший характерный масштаб ![]() , чем крупномасштабная вихревая структура. Заметим, что проделанные здесь оценки для характерных масштабов крупномасштабной неустойчивости справедливы при выполнении условия
, чем крупномасштабная вихревая структура. Заметим, что проделанные здесь оценки для характерных масштабов крупномасштабной неустойчивости справедливы при выполнении условия ![]() , т. е. когда характерный масштаб турбулентности
, т. е. когда характерный масштаб турбулентности ![]() и стратификации
и стратификации ![]() примерно равны:
примерно равны: ![]() , а характерный временной масштаб турбулентности:
, а характерный временной масштаб турбулентности:
![]()
Зная определение джинсовой частоты ![]() можно оценить плотность галактической среды:
можно оценить плотность галактической среды:![]() . Это типичная плотность для галактических дисков [6, 27].
. Это типичная плотность для галактических дисков [6, 27].
Применяя асимптотический метод многих масштабов, получены условия возникновения крупномасштабной неустойчивости во вращающейся стратифицированной самогравитирующей электропроводящей среде при наличии внешней мелкомасштабной силы с нулевой спиральностью и малым числом Рейнольдса. Это условие позволило использовать число Рейнольдса в качестве малого параметра асимптотического разложения. В нулевом порядке теории возмущений показана возможность генерации спиральности мелкомасштабного поля скорости (или спиральной турбулентности) во вращающейся стратифицированной самогравитирующей элекропроводящей среде в результате действия внешней неспиральной силы [25]. Именно этот факт приводит к возникновению крупномасштабной неустойчивости типа ![]() -эффекта, вследствие которого происходит генерация крупномасштабных вихревых и магнитных возмущений. Причем темпы роста магнитных возмущений выше, чем у вихревых. Мелкомасштабные пульсации магнитного поля, возбуждаемые стационарным источником с нулевой спиральностью, оказывают влияние на эволюцию крупномасштабных возмущений. В этом случае меняется порог крупномасштабных неустойчивостей и на Рис. 7 показаны области где проявляется гидродинамический и магниогидродинамический
-эффекта, вследствие которого происходит генерация крупномасштабных вихревых и магнитных возмущений. Причем темпы роста магнитных возмущений выше, чем у вихревых. Мелкомасштабные пульсации магнитного поля, возбуждаемые стационарным источником с нулевой спиральностью, оказывают влияние на эволюцию крупномасштабных возмущений. В этом случае меняется порог крупномасштабных неустойчивостей и на Рис. 7 показаны области где проявляется гидродинамический и магниогидродинамический ![]() -эффекты. С ростом амплитуды эти неустойчивости выходят на нелинейную стадию и формируют стационарные крупномасштабные структуры. Исследование этих вопросов можно провести также с использованием метода многих масштабов [16].
-эффекты. С ростом амплитуды эти неустойчивости выходят на нелинейную стадию и формируют стационарные крупномасштабные структуры. Исследование этих вопросов можно провести также с использованием метода многих масштабов [16].
Литература:
- Штеенбек М., Краузе Ф. Возникновение магнитных полей звезд и планет в результате турбулентного движения их веществ. // Магнитная гидродинамика. 1967. № 3. С. 19–44.
- Моффат Г. Возбуждение магнитного поля в проводящей среде. М.: Мир. 1980. 343 с.
- Зельдович Я. Б., Рузмайкин А. А., Соколов Д. Д. Магнитные поля в астрофизике. Инст. комп. иссл. РХД.: Ижевск. 2006. 384 с.
- Паркер Ю. Беседы об электрических и магнитных полях в космосе. Инст. комп. иссл. РХД.: Ижевск. 2010. 208 с.
- Краузе Ф., Рэдлер К.-Х. Магнитная гидродинамика средних полей и теория динамо. М.: Мир. 1984. 314 с.
- Рузмайкин А. А., Соколов Д. Д., Шукуров А. М. Магнитные поля галактик. М.: Наука. 1988. 279 с.
- Соколов Д. Д., Степанов Р. А., Фрик П. Г. Динамо на пути от астрофизических моделей к лабораторному эксперименту. // УФН. 2014. Т. 184. С. 318–335.
- Моисеев С. С., Оганян К. Р., Руткевич П. Б., Тур А. В., Хоменко Г. А., Яновский В. В. Вихревое динамо в спиральной турбулентности. В сб.: Интегрируемость и кинетические уравнения для солитонов. Наук. Думка: Киев. 1990. С. 280–382.
- Моффат Г. Некоторые направления развития турбулентности. Соврем. гидродинамика. Успехи и проблемы. М.: Мир. 1984. С. 48–76.
- Krause F., Rudiger G. On the Reynolds stresses in mean-field hydrodynamics. I. Incompressible homogeneous isotropic turbulence. // Astron. Nachr. 1974. V. 295. P. 93–99.
- Моисеев С. С., Сагдеев Р. З., Тур А. В., Хоменко Г. А., Яновский В. В. Теория возникновения крупномасштабных структур в гидродинамической турбулентности. // ЖЭТФ. 1983. Т. 85. С. 1979–1987.
- Петросян А. С. Дополнительные главы теории турбулентности. Спиральная турбулентность. Москва: ИКИ РАН. 2013. 60 с.
- Moiseev S. S., Rutkevitch P. B., Tur A. V., Yanovsky V. V. Vortex dynamos in a helical turbulent convection. // Sov. Phys. JETP. 1988. V. 67. P. 294–303.
- Новиков Е. А. Функционалы и метод случайных сил в теории турбулентности. // ЖЭТФ. 1964. Т. 47. Вып. 5(11). С.1919–1926.
- Кляцкин В. И. Стохастические уравнения и волны в случайно-неоднородных средах. М.: Наука. 1980. 337 с.
- Frishe U., She Z. S., Sulem P. L. Large Scale Flow Driven by the Anisotropic Kinetic Alpha Effect. // Physica D. 1987. V. 28. P. 382.
- Дружинин О. А., Хоменко Г. А. Нелинейная теория гидродинамического альфа-эффекта в сжимаемой среде и обратный каскад энергии. В тр. Межд. конф.: Нелинейные и турбулентные процессы в физике. Киев: Наук. думка. 1982. Т. 2. С. 83–86.
-
Rutkevitch P. B., Sagdeev R. Z., Tur A. V., Yanovsky V. V. Nonlinear dynamic theory of the
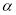 -effect in compressible fluid. Proceeding of the IV Intern. Workshop on Nonlinear and Turb. Pros. in Physics. Kiev.1989. V. 2. P. 172–175.
-effect in compressible fluid. Proceeding of the IV Intern. Workshop on Nonlinear and Turb. Pros. in Physics. Kiev.1989. V. 2. P. 172–175.
- Tur A. V., Yanovsky V. V. Large-scale instability in hydrodynamics with stable temperature stratification driven by small-scale helical force. ArXiv:1204.5024 V.1 [physics. Flu-dyn.] (2012).
- Tur A. V., Yanovsky V. V. Non Linear Vortex Structure in Stratified Driven by Small- scale Helical Forse. // Open Journal of Fluid Dynamics. 2013. V. 3. P. 64–74.
- Копп М. И., Тур А. В., Яновский В. В. Крупномасштабная конвективная неустойчивость в электропроводящей среде с мелкомасштабной спиральной турбулентностью. // ЖЭТФ. 2015.Т. 147. С. 846–866.
- Kopp M., Tur A., Yanovsky V. The Large Scale Instability in Rotating Fluid with Small Scale Force // Open Journal of Fluid Dynamics. 2015. V. 5. P. 128–138.
- Kopp M., Tur A., Yanovsky V. Nonlinear Vortex Structures in Obliquely Rotating Fluid. // Open Journal of Fluid Dynamics. 2015. V. 5. P. 311–321.
- Копп М. И. Крупномасштабное магнитовращательное динамо. I. Линейная теория без внешнего магнитного поля // Альманах современной науки и образования. 2016. № 4 (106). С. 59–73.
- Копп М. И. Генерация крупномасштабных вихревых структур во вращающейся самогравитирующей среде с мелкомасштабной неспиральной силой // Молодой ученый. 2016. № 11(115). С. 101–110.
- Чхетиани О. Г. Самоорганизация и турбулентность в отражательно-несимметричных плазменно-гидродинамических средах. Дисс. на соиск. уч. степени докт. физ.-мат. наук. Москва. 1999. 262 с.
- Рольфс К. Лекции по теории волн плотности. М.: Мир. 1980. 205 с.
- Долгинов А. З., Урпин В. А. Термомагнитная неустойчивость неоднородной плазмы. // ЖЭТФ. 1978. Т. 77. С. 1921–1932.
- Вайнштейн С. И., Зельдович Я. Б., Рузмайкин А. А. Турбулентное динамо в астрофизике. М.: Наука.1980. 354 с.
- Вайнштейн С. И. Магнитные поля в космосе. М.: Наука.1983. 237 с.
- Montgomery D., Chen H. Turbulent amplification of large-scale magnetic fields. // Plasma Physics and Controlled Fusion. 1984. V. 26. № 10. P. 1199–1210.
- Rudiger G. On the α-Effect for Slow and Fast Rotation. // Astron. Nachr. 1978. V.299. № 4. P. 217–222.







