В данной работе проводится анализ математической модели взаимодействия агентов коррупционного процесса в условиях неполной информации. Описан алгоритм нахождения нормальной формы игры с неполной информацией и оптимальных стратегий участников. Найдены средние ожидаемые выигрыши участников коррупционной сделки в конечно повторяющейся игре с неполной информацией. Анализ модели проведен с помощью инструментов теории игр с неполной информацией.
Ключевые слова: коррупционная сделка, игра с неполной информацией, средний ожидаемый выигрыш
Исследования в области описания коррупционных процессов с помощью построения математических моделей возникли в 70х годах 20ого века [3]. В работе рассматривается математическая модель взаимодействия участников коррупционной сделки в условиях асимметрии информации. Асимметрия информации означает, что один из участников обладает «большей» информацией или имеет доступ к ней в то время, как остальные участники обладают «меньшей» информацией или не обладают ей вовсе.
Постановка задачи
Рассматривается процесс заключения коррупционной сделки между агентами в условиях неполной информации.
Пусть:
![]() — множество агентов, участвующих в коррупционной сделке.
— множество агентов, участвующих в коррупционной сделке.
![]() — множество коррупционных эпизодов, возникающих в следствии асимметрии информации.
— множество коррупционных эпизодов, возникающих в следствии асимметрии информации.
![]() — множество стратегий
— множество стратегий ![]() - ого агента в коррупционном эпизоде
- ого агента в коррупционном эпизоде ![]() .
.
![]() — функция выигрыша
— функция выигрыша ![]() - ого агента в коррупционном эпизоде
- ого агента в коррупционном эпизоде ![]() .
.
Формализация модели
Рассматривается модель, в которой взаимодействуют два агента: коррумпированный Чиновник и Клиент. В процессе этого взаимодействия, Чиновник и Клиент заключают коррумпированную сделку, следуя которой Клиент платит Чиновнику сумму в определенном размере. Чиновник также заинтересован в получении взятки.
Следуя данной модели, Чиновник стремится максимизировать размер взятки, а Клиент стремится минимизировать размер предлагаемой взятки. Процесс заключения сделки между Чиновником и Клиентом проходит одним из двух способов: ![]() или
или ![]() . Каждый участник решает, каким именно способом он хочет провести сделку. Пусть буква «
. Каждый участник решает, каким именно способом он хочет провести сделку. Пусть буква «![]() » означает, что сделка проводится первым способом, а буква «
» означает, что сделка проводится первым способом, а буква «![]() », что сделка проводится вторым способом. Если агенты решают провести сделку разными способами, то коррупционная сделка не совершается.
», что сделка проводится вторым способом. Если агенты решают провести сделку разными способами, то коррупционная сделка не совершается.
Неопределенность ситуации заключается в том, что размер взятки зависит от предпочтений Чиновника. Пусть Чиновник имеет два типа предпочтений ![]() . Пусть в роли коррупционных эпизодов выступают тип предпочтений Чиновника.
. Пусть в роли коррупционных эпизодов выступают тип предпочтений Чиновника.
Рассмотрим два коррупционных эпизода ![]() и
и ![]() . В коррупционном эпизоде
. В коррупционном эпизоде ![]() предпочтения Чиновника принадлежат к первому типу, а в
предпочтения Чиновника принадлежат к первому типу, а в ![]() принадлежат ко второму типу. Пусть тип предпочтений Чиновника принадлежит к первому типу с вероятностью равной
принадлежат ко второму типу. Пусть тип предпочтений Чиновника принадлежит к первому типу с вероятностью равной ![]() .
.
Предполагается, что Клиент не осведомлен о предпочтениях Чиновника. Коррупционные эпизоды ![]() и
и ![]() представлены в виде игры в нормальной форме [4]. Числа в ячейках матрицы обозначают размер взятки, которую Клиент передаст Чиновнику (Таблица 1.).
представлены в виде игры в нормальной форме [4]. Числа в ячейках матрицы обозначают размер взятки, которую Клиент передаст Чиновнику (Таблица 1.).
Таблица 1
|
Клиент |
|
|||
|
|
|
|||
|
Чиновник |
|
3 |
0 |
|
|
|
0 |
0 |
||
|
Клиент |
|
|||
|
|
|
|||
|
Чиновник |
|
0 |
0 |
|
|
|
0 |
2 |
||
Представим коррупционные эпизоды ![]() и
и ![]() в развернутой форме в виде игры
в развернутой форме в виде игры ![]() , где левая ветвь графа описывает коррупционный эпизод
, где левая ветвь графа описывает коррупционный эпизод ![]() , а правая ветвь графа коррупционный эпизод
, а правая ветвь графа коррупционный эпизод ![]() (Рисунок 1.)
(Рисунок 1.)
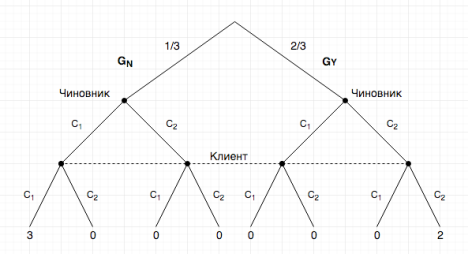
Рис. 1.
Оптимальные стратегии чиновника при совершении одной сделки
Значение игры
Рассмотрим нормальную форму игры ![]() (Таблица 2.), в которой Чиновник имеет 4 стратегии: {
(Таблица 2.), в которой Чиновник имеет 4 стратегии: {![]() ,
, ![]() ,
, ![]() ,
, ![]() }, в которых, например (
}, в которых, например (![]() ), означает что Чиновник в коррупционном эпизоде
), означает что Чиновник в коррупционном эпизоде ![]() выбирает стратегию
выбирает стратегию ![]() , а в коррупционном эпизоде
, а в коррупционном эпизоде ![]() стратегию
стратегию ![]() . [1] Клиент имеет только 2 стратегии {
. [1] Клиент имеет только 2 стратегии {![]() ,
, ![]() }. В ячейках матрицы обозначены ожидаемые выигрыши Чиновника:
}. В ячейках матрицы обозначены ожидаемые выигрыши Чиновника:
Пусть ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Таблица 2
|
Клиент |
|||
|
Чиновник |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вторая строка в матрице игры (Таблица 2.) доминирует первую, третью и четвертую. Так как ![]() , то ожидаемый выигрыш Чиновника(значение игры) в игре
, то ожидаемый выигрыш Чиновника(значение игры) в игре ![]() обозначим за
обозначим за ![]() . Стратегия
. Стратегия ![]() является оптимальной. [2]
является оптимальной. [2]
На Рисунке 2. представлены оптимальные стратегии Чиновника и Клиента. Пунктир на Рисунке 2. означает, что Клиент не знает предпочтений Чиновника.
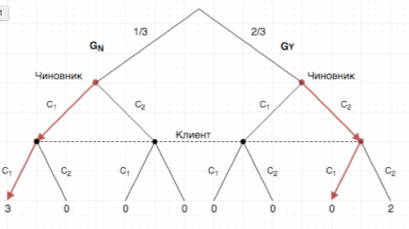
Рис. 2.
Стрелки на графе показывают оптимальные стратегии Чиновника и Клиента. Обозначим за ![]() — выигрыш Чиновника, если оба участника следуют оптимальным стратегиям в коррупционном эпизоде
— выигрыш Чиновника, если оба участника следуют оптимальным стратегиям в коррупционном эпизоде ![]() , а за
, а за ![]() — выигрыш Чиновника, если оба участника следуют оптимальным стратегиям в коррупционном эпизоде
— выигрыш Чиновника, если оба участника следуют оптимальным стратегиям в коррупционном эпизоде ![]() .
.
![]() ;
;
Напомним, что ![]() .
.
![]()
![]()
Оптимальные стратегии чиновника и клиента при совершении n- сделок
Рассмотрим коррупционный эпизод, в котором Чиновник и Клиент должны заключить несколько сделок в один день. Таким образом, коррупционный эпизод ![]() или
или ![]() будет повторяться
будет повторяться ![]() — раз, где
— раз, где ![]() — количество сделок, совершенных в определенный день. Чиновник после совершения каждой сделки, Клиент будет точно знать какую стратегию выбрал Чиновник и объем взятки.
— количество сделок, совершенных в определенный день. Чиновник после совершения каждой сделки, Клиент будет точно знать какую стратегию выбрал Чиновник и объем взятки.
Рассмотрим случай, в котором Чиновник будет пользоваться оптимальными стратегиями, предписанными ему в ![]() , а именно, выбирать стратегию
, а именно, выбирать стратегию ![]() , если перед ним коррупционный эпизод
, если перед ним коррупционный эпизод ![]() и стратегию
и стратегию ![]() , если перед ним коррупционный эпизод
, если перед ним коррупционный эпизод ![]() . Если
. Если ![]() — номер сделки и если
— номер сделки и если ![]() , тогда
, тогда ![]() представляется в развернутой форме как (Рисунок 3.):
представляется в развернутой форме как (Рисунок 3.):
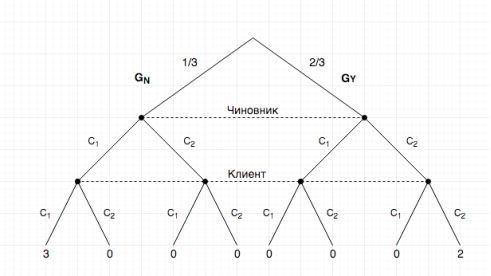
Рис. 3.
Клиенту известны стратегии и выигрыши Чиновника. Таким образом, если Чиновник при совершении первой сделки пользуется оптимальными стратегиями, то Клиент немедленно узнает предпочтения Чиновника.
Рассмотрим совершение второй сделки ![]() , в которой Клиент точно знает, какой перед ним коррупционный эпизод
, в которой Клиент точно знает, какой перед ним коррупционный эпизод ![]() или
или ![]() (Рисунок 4.):
(Рисунок 4.):
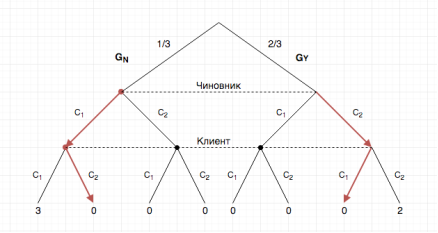
Рис. 4.
Ожидаемый выигрыш Чиновника в любой из двух ситуаций будет равен нулю.
Пусть ![]() — средний ожидаемый выигрыш Чиновника при совершении сделок в количестве
— средний ожидаемый выигрыш Чиновника при совершении сделок в количестве ![]() , тогда:
, тогда:
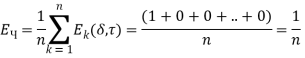 (1)
(1)
где:
– ![]() - количество совершаемых сделок;
- количество совершаемых сделок;
– ![]() - ожидаемый выигрыш Чиновника при совершении k-ой сделки, если Чиновник использовал стратегию
- ожидаемый выигрыш Чиновника при совершении k-ой сделки, если Чиновник использовал стратегию ![]() , а Клиент стратегию
, а Клиент стратегию ![]() ;
;
Таким образом, средний ожидаемый выигрыш Чиновника стремится к значению ![]() или
или ![]() .
.
Пусть рассматривается ситуация, в которой Чиновник игнорирует свои предпочтения в размере взятки. Выигрыши и стратегии Чиновника и Клиента остаются прежними и этот коррупционный эпизод обозначен как
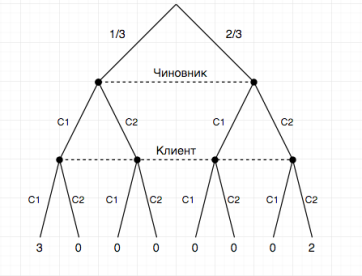
Рис. 5. Игра ![]()
Нормальная форма ![]() (Таблица 3.), в которой Чиновник игнорирует свои предпочтения:
(Таблица 3.), в которой Чиновник игнорирует свои предпочтения:
Таблица 3
|
Клиент |
|||
|
Чиновник |
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]()
Таблица 4
|
Клиент |
|||
|
Чиновник |
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, Чиновник будет выбирать стратегию ![]() с вероятностью
с вероятностью ![]() , а стратегию
, а стратегию ![]() с вероятностью
с вероятностью ![]() . Клиент будет следовать тем же смешанным стратегиям (Таблица 4.). Обозначим за
. Клиент будет следовать тем же смешанным стратегиям (Таблица 4.). Обозначим за ![]() ожидаемый выигрыш Чиновника (значение игры
ожидаемый выигрыш Чиновника (значение игры ![]() ) в
) в ![]() , тогда
, тогда ![]() .
.
Обозначим за ![]() ожидаемый выигрыш Чиновника в игре
ожидаемый выигрыш Чиновника в игре ![]() , а за
, а за ![]() — ожидаемый выигрыш Чиновника в ситуации
— ожидаемый выигрыш Чиновника в ситуации ![]() .
.
– Пусть ![]() –матрица выигрышей Чиновника в
–матрица выигрышей Чиновника в ![]() :
:
– Пусть ![]() –матрица выигрышей Чиновника в
–матрица выигрышей Чиновника в ![]() :
:
![]()
– Пусть ![]() - вектор смешанных стратегий Чиновника, а
- вектор смешанных стратегий Чиновника, а
![]() - вектор смешанных стратегий Клиента.
- вектор смешанных стратегий Клиента.
Тогда, ![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Рассмотрим случай, в котором Чиновник будет пользоваться стратегиями, описанными выше, в коррупционном эпизоде ![]() , тогда его средний ожидаемый выигрыш будет
, тогда его средний ожидаемый выигрыш будет ![]() (
(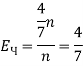 ). Так как -целое число, то при
). Так как -целое число, то при ![]() .
.
Напомним, что ![]() . Получаем
. Получаем ![]()
![]() , а
, а ![]() .
.
Вывод: Если Чиновник игнорирует свои предпочтения в размере взятки, то при заключении коррумпированных сделок в количестве равном ![]() , его средняя ожидаемая прибыль от этих сделок, будет выше чем средняя ожидаемая прибыль, если бы Чиновник следовал своим предпочтениям.
, его средняя ожидаемая прибыль от этих сделок, будет выше чем средняя ожидаемая прибыль, если бы Чиновник следовал своим предпочтениям.
Проверка секретности информации, доступной чиновнику, при совершении n сделок
Проверим, что Чиновник, пользуясь стратегиями, описанными в
Рассмотрим коррупционный эпизод ![]() и
и ![]() со стороны Клиента. Пусть Клиент после совершения первой сделки, оценивает вероятность возникновения коррупционного эпизода
со стороны Клиента. Пусть Клиент после совершения первой сделки, оценивает вероятность возникновения коррупционного эпизода ![]() и
и ![]() .
.
Клиент знает, что Чиновник будет выбирать стратегию ![]() с вероятностью
с вероятностью ![]() , а стратегию
, а стратегию ![]() с вероятностью
с вероятностью ![]() . Клиент оценивает вероятность возникновениякоррупционного эпизода
. Клиент оценивает вероятность возникновениякоррупционного эпизода ![]() и
и ![]() , пользуясь формулами условной вероятности.
, пользуясь формулами условной вероятности.
Рассмотрим стратегии Чиновника при совершении ![]() -ой сделки (Рисунок 6.). Пусть
-ой сделки (Рисунок 6.). Пусть ![]() - вероятность, с которой Чиновник выбирает стратегию
- вероятность, с которой Чиновник выбирает стратегию ![]() в коррупционном эпизоде
в коррупционном эпизоде ![]() , а
, а ![]() - вероятность, с которой Чиновник выбирает стратегию
- вероятность, с которой Чиновник выбирает стратегию ![]() в коррупционном эпизоде
в коррупционном эпизоде ![]() .
. ![]() - вероятность появления коррупционного эпизода
- вероятность появления коррупционного эпизода ![]() .(
.(![]() )
)
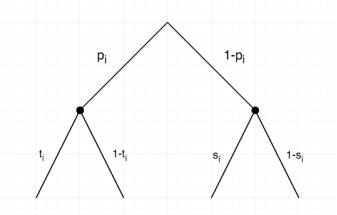
Рис. 6.
Рассмотрим первую коррупционную сделку, то есть ![]() (Рисунок 7.).
(Рисунок 7.).
![]() ;
;
![]() ;
;
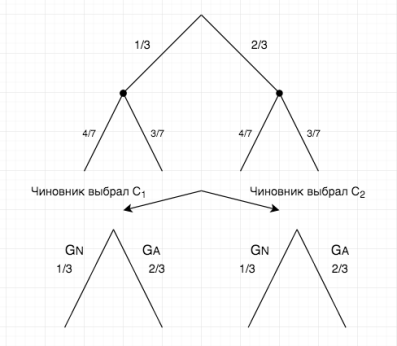
Рис. 7.
Таким образом, если после каждой коррупционной сделки, Клиент оценивает вероятность появления коррупционного эпизода
Вывод
В работе проведен анализ математической модели взаимодействия коррумпированного чиновника и клиента в условиях асимметрии информации. В роли информации в данной модели выступают вкусы и предпочтения одного из игроков. Рассмотрен конкретный пример и сделан вывод, что в конечно повторяющейся игре с неполной информацией игрок, обладающий информацией, должен действовать, не опираясь на свои предпочтения.
Литература:
- Guillermo Ordonez Notes on Bayesian Games URL: http://www.sas.upenn.edu/~ordonez/pdfs/ECON %20201/NoteBAYES.pdf
- Robert J. Aumann Repeated games with incomplete information Robert/J. Aumann and Michael B. Mashler with collaboration of Richard B. Strearns — MIT Press. 1995. — 323 p.
- Зенюк Д. А., Малинецкий Г. Г., Фаллер Д. С. Социальная модель коррупции в иерархических структурах // Препринты ИПМ им. М. В. Келдыша. 2013. № 87. 27 с. URL: http://library.keldysh.ru/preprint.asp?id=2013–87
- Петросян, Л. А. Теория игр / Л. А. Петросян, Н. А. Зенкевич,
- Е. А. Семина. — М.: Высшая школа, 1998. — 304 с.







