Суда с малой площадью ватерлинии (далее СМПВ) представляют собой разновидность катамарана, опирающуюся на два полностью погруженных корпуса. Подобная конструкция позволяет без особых усилий преодолевать бортовую качку, однако при определенной скорости суда данной конструкции могут терять устойчивость в вертикальной плоскости. Это происходит из-за так называемого «эффекта Мунка», который заставляет судно крениться на корму. Для предотвращения возникновения этого эффекта необходимо грамотное применение стабилизирующих рулей, что и является предметом данной работы.
Для формализации поставленной задачи необходимо рассмотреть математическую модель движения СМПВ. Используя второй закон Ньютона и разложение в ряд Тейлора для обеспечения линейности уравнений, получаем следующее представление движений судна [1]:
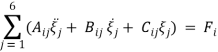
где ![]() продольное смещение судна,
продольное смещение судна, ![]() — поперечное смещение судна,
— поперечное смещение судна, ![]() — вертикальное смещение судна,
— вертикальное смещение судна, ![]() — крен,
— крен, ![]() — дифферент,
— дифферент, ![]() — курс (рис. 1),
— курс (рис. 1), ![]() — возмущающие силы и моменты волн,
— возмущающие силы и моменты волн, ![]() — сумма матрицы массы и матрицы присоединенных масс,
— сумма матрицы массы и матрицы присоединенных масс, ![]() — матрица демпфирования,
— матрица демпфирования, ![]() — матрица восстанавливающих сил (restoring forces).
— матрица восстанавливающих сил (restoring forces).
Учитывая продольную симметрию данного типа судов, а также линейности уравнений становится возможным выделить уравнения движения СМПВ в вертикальной плоскости:
![]()
![]()
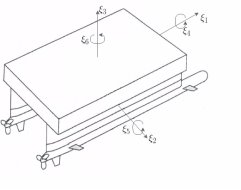
Рис. 1. Система координат
Теперь становится возможным переписать эти уравнения в матричной форме, добавив гидродинамические коэффициенты при стабилизирующих рулях:

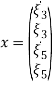
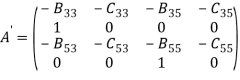
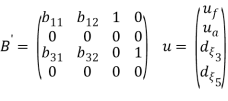
![]()
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() — углы отклонения переднего и заднего стабилизирующего руля а также силы и моменты, задействованные в их активации и влияющие на вертикальное движение судна.
— углы отклонения переднего и заднего стабилизирующего руля а также силы и моменты, задействованные в их активации и влияющие на вертикальное движение судна.
В итоге данные уравнения запишутся в виде ![]() , которые в свою очередь очевидными алгебраическими преобразованиями приводятся к классической форме модели в пространстве состояний:
, которые в свою очередь очевидными алгебраическими преобразованиями приводятся к классической форме модели в пространстве состояний:
![]()
![]()
Коэффициенты матрицы управления B определяются следующим образом [5]:
![]() ;
; ![]()
![]() ;
; ![]()
Основная особенность данной модели состоит в том, что её коэффициенты заданы в частотной области и зависят от многих параметров, большинство из которых невозможно учесть явно [2]. Поэтому при моделировании пользуются одним из основных частотных показателей судна в условиях волнения: частотой встречи
![]()
где U — собственная скорость судна по курсу, ![]() — частота волнения моря/океана,
— частота волнения моря/океана, ![]() — угол между курсом судна и направлением волнения (0° для курса по волнам и 180° для курса строго против волн). Следовательно, для использования данной модели должна быть выбрана определенная частота
— угол между курсом судна и направлением волнения (0° для курса по волнам и 180° для курса строго против волн). Следовательно, для использования данной модели должна быть выбрана определенная частота ![]() .
.
Для универсализации модели в нее включают параметрическую неопределенность, которая вычисляется следующим образом: в первую очередь частота волнения дискретизируется в некотором диапазоне. Затем вычисляется частота встречи, основываясь на основных скоростных режимах рассматриваемого судна и интересующего угла ![]() . Для каждого значения
. Для каждого значения ![]() вычисляются коэффициенты модели в пространстве состояний и составляется диапазон вариаций каждого коэффициента. Затем рассматривается уже возмущенная модель вида:
вычисляются коэффициенты модели в пространстве состояний и составляется диапазон вариаций каждого коэффициента. Затем рассматривается уже возмущенная модель вида:
![]()
![]()
Здесь коэффициенты с индексом n обозначают номинальные значения и равны среднему значению среди всех вычисленных вариантов соответствующих коэффициентов, а коэффициенты с индексом r равны половине диапазона возможных значений. ![]() представляют собой изменения соответствующего коэффициента и ограничены по норме (
представляют собой изменения соответствующего коэффициента и ограничены по норме (![]() ).
).
Теперь, для применения современных методов теории робастности, необходимо представить систему в виде номинальной модели, замкнутой обратной связью с неопределенностями в коэффициентах (![]() представление). Это выполняется с помощью верхнего дробно-линейного преобразования (рис. 2):
представление). Это выполняется с помощью верхнего дробно-линейного преобразования (рис. 2):
![]()
где
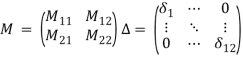
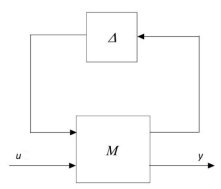
Рис. 2. ![]() конфигурация
конфигурация
Матрица M представляет собой комбинацию номинальной модели и границы вариаций её коэффициентов.
![]()
После построения модели для синтеза управления применялся ![]() и
и ![]() синтез, которые позволяют учесть указанную параметрическую неопределенность.
синтез, которые позволяют учесть указанную параметрическую неопределенность.
В частности, в рамках данной работы была рассмотрена модель СМПВ судна водоизмещением 400 тонн (CHINA 2001), введенная в [4], и произведено моделирование в среде MATLAB.
Номинальные коэффициенты модели следующие:
![]()

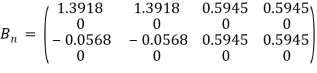
![]()
![]()
Вариации соответствующих коэффициентов указаны в таблице 1.
Таблица 1
Вариации коэффициентов модели
|
|
0.0626 |
|
|
1.7952 |
|
|
0.1149 |
|
|
8.4392 |
|
|
0.0004 |
|
|
0.1656 |
|
|
-0.0215 |
|
|
-0.9618 |
|
|
0.2784 |
|
|
0.2784 |
|
|
0.0114 |
|
|
0.0114 |
Затем была составлена ![]() -
-![]() конфигурация. Блок M состоит из номинальной модели и вариаций её коэффициентов:
конфигурация. Блок M состоит из номинальной модели и вариаций её коэффициентов:
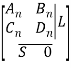
где ![]() ,
, ![]() — вектор-строка размерности
— вектор-строка размерности ![]() . Если обозначить ненулевые элементы
. Если обозначить ненулевые элементы ![]() в виде
в виде ![]() , то все элементы матрицы
, то все элементы матрицы ![]() равны нулю, кроме
равны нулю, кроме ![]() ,
, 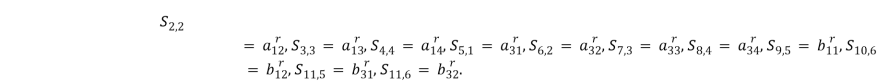 Блок
Блок ![]() , где
, где ![]() для
для ![]() и
и ![]() для
для ![]() .
. ![]() ,
, ![]() .
.
Номинальная модель устойчива (все её собственные значения лежат в левой открытой полуплоскости), однако существуют возмущения, способные сделать движение неустойчивым. Отсюда следует, что необходим синтез регулятора, обеспечивающего робастную устойчивость и качество динамического процесса замкнутой системы. Разумно применить ![]() — синтез.
— синтез.
Для этого сначала необходимо задать весовые функции ![]() и
и ![]() , которые будут определять качество динамического процесса и ограничения на управляющие элементы [3]. В данном случае, угол отклонения рулей не должен превышать
, которые будут определять качество динамического процесса и ограничения на управляющие элементы [3]. В данном случае, угол отклонения рулей не должен превышать ![]() .
. ![]() представляет собой диагональную передаточную матрицу размерности
представляет собой диагональную передаточную матрицу размерности ![]() :
:
![]()
где соответствующие элементы
График амплитудно-частотной характеристики данных весовых функций представлен на рисунке 3.
В свою очередь, ![]() — диагональная передаточная матрица
— диагональная передаточная матрица ![]() , c постоянными элементами, которые отражают масштабирование сигнала
, c постоянными элементами, которые отражают масштабирование сигнала ![]() в соответствии с наложенными ограничениями.
в соответствии с наложенными ограничениями.
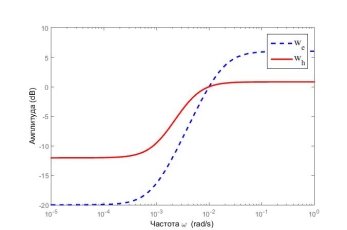
Рис. 3: АЧХ весовых функций
Полученный регулятор стабилизирует номинальную модель и отвечает требованиям качества динамического процесса: амплитуда в режиме с ненулевым волнением выходного сигнала замкнутой системы в несколько раз ниже, чем у разомкнутой системы при соблюдении ограничений на динамику рулей (рис. 4), однако система не отвечает требованиям робастной устойчивости. Так как ![]() , то должно выполняться [7]:
, то должно выполняться [7]:
![]()
![]()
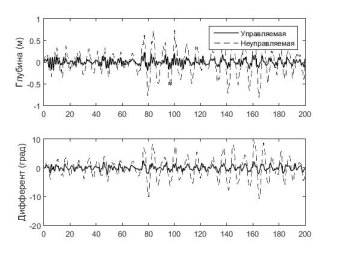
Рис. 4. Реакция на волнение в 3 балла

Рис. 5. Реакция на волнение в 5 баллов
где ![]() называется структурированным сингулярным числом системы. Однако верхняя граница структурированного сингулярного числа больше 1 на некоторых частотах, что означает, что существуют такие возмущения
называется структурированным сингулярным числом системы. Однако верхняя граница структурированного сингулярного числа больше 1 на некоторых частотах, что означает, что существуют такие возмущения ![]() , которые могут сделать систему неустойчивой.
, которые могут сделать систему неустойчивой.
Следовательно, нужно расширить границы робастной устойчивости с помощью ![]() синтеза методом D-K итераций, используя регулятор, полученный при
синтеза методом D-K итераций, используя регулятор, полученный при ![]() синтезе в качестве начального для алгоритма. В итоге был выбран регулятор, полученный на 10 итерации с минимальной достигнутой границей структурированного сингулярного числа равной 0.8951, который был редуцирован до 9 порядка. Результат его работы для волнения в 5 баллов можно видеть на рисунке 5.
синтезе в качестве начального для алгоритма. В итоге был выбран регулятор, полученный на 10 итерации с минимальной достигнутой границей структурированного сингулярного числа равной 0.8951, который был редуцирован до 9 порядка. Результат его работы для волнения в 5 баллов можно видеть на рисунке 5.
В результате данной работы был проведен синтез управления, которое отвечает требованиям робастной устойчивости и обеспечивает меньшую амплитуду управляемого выходного сигнала по сравнению с неуправляемым. Следовательно, примененные методы решают поставленную задачу и могут использоваться для обеспечения устойчивости вертикального движения СМПВ в условиях волнения.
Литература:
- Chinn N. L., Roberts G. N., Scrace R. G., Owens D. H. Mathematical modelling of a small waterplane area twin hulled (SWATH) vessel // Control’94 International Conference. 1994. № 2. С. 1560–1565.
- Dubrovsky V. A., Matveev K., Sutulo S. Small waterplane area ships. Backbone Publishing Company, 2007. 255 с.
- Gu D. W., Petkov P.Hr., Konstantinov M. M. Robust Control Design with MATLAB. Springer, 2005. 389 с.
- Lihua Liang, Baohua Wang, Ming Ji Adaptive Fuzzy Control for SWATH Ship Seakeeping Characteristics // International Conference on Mechatronics and Automation. 2012. С. 440–445.
- Omar Bin Yaakob Development of a semi-SWATH craft for Malaysian waters. Malaysia: University of Technology, 2006. 198 с.
- Веремей Е. И. Линейные системы с обратной связью. СПб.: Лань, 2013. 445 с.







