Рассмотрим свободные колебания упругого пространства, имеющего цилиндрическую полость.
We shall Consider the own fluctuations cylindrical of the hole in boundless springy ambience.
Рассмотрим свободные колебания упругого пространства, имеющего цилиндрическую полость. Эту задачу будем решать с использованием потенциалов в цилиндрической системе координат. Волновые уравнения имеют вид [1]:
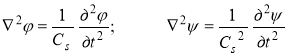 (1)
(1)
где и — являются потенциалами перемещения, Ср и Сs- фазовые скорости распространения волн расширения и сдвига. Предполагаем, что при r=a поверхностьцилиндрической полости свободна от напряжения, т. е.
rr|r=a= r|r=a=0. (2)
При собственных колебаниях на бесконечности ставятся укороченные условия Зоммерфельда, т. е.
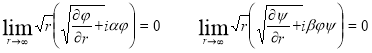 .
.
Решение уравнения (1) ищется в виде
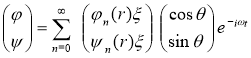 , (3)
, (3)
где - частота; n-число волн; t-время;
Подставляя (3) в (1), получим уравнения Гельмгольца, решения которых имеет вид:
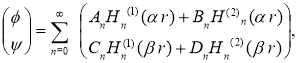 (4)
(4)
где Hn(1),(2) (z) — функции Ханкеля 1-го и 2-го рода n-го порядка; =ω/ср и =ω/Сs — волновые числа; An, Bn, Cn, Dn, — произвольные постоянные, которые определяются из граничных условий (2).
Из условия (2) следует, что ![]() (z) описывает сходящуюся волну, поэтому решения (4) примет вид
(z) описывает сходящуюся волну, поэтому решения (4) примет вид
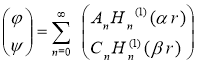 (5)
(5)
После подстановки (5) в граничные условия (2) получим систему алгебраических уравнений с комплексными коэффициентами
[D] {q}=0, (6)
где {q}={An, Cn} — вектор столбец произвольных постоянных; [с] — квадратная матрица, элементы которой выражаются через функции Ханкеля первого рода n-го порядка. Для того, чтобы система (6) имела нетривиальное решение необходимо и достаточно
[с]=0. (7)
Корни трансцендентного (7) уравнения описывают частоту собственных колебаний полости. Частотное уравнение (7) принимает следующий вид:
Dp = xHp-1 ([(p2–1)yHp-1 (y)-(p3-p+y2/2) Hp (y)] –
—Hp(x) [(p3-p+y2/2) y Hp-1(y) — (p2+p-y2/4)y2Hp(y)],(8)
где
= wa (ρ/(+2))1/2; y = wa (ρ/) 1/2,
и -коэффициенты Ляме; ρ- плотность материала.
Уравнение (8) после некоторых преобразований можно записать в следующим виде:
(p2–1) F(x) F(y)-(y2/2) (F(x)+F(y)+p2-(p2-y2/2)2=0,
где F(x) = xHp1(x)/Hp(x), р = 1, 2, 3… (9)
Сопровождаемые излучением продольных звуковых волн, что приводит к потере энергии, и тем самым, к затуханию колебаний. При Ср >> СS рассматриваемая задача эквивалентна задаче о собственных колебаниях тела. Частотное уравнение (9) принимает следующий вид:
![]() , отсюда
, отсюда ![]()
где k = ω / Ср, а — радиус.
Корни характеристического уравнения (9) находим по методу Мюллера [1].
Таблица 1 (=0,25)
|
№ |
Наши результаты |
Рао и ow [1] |
B nronиParnes [2] |
|
0 |
0,44741–0.44420 i |
0.44647–0.44127 i |
0.4464–0.4410 i |
|
1 |
1,09272–0,77653 i |
1.09272–0.7653 i |
1.0929–0.441 i |
|
2 |
1,907554–0,89782 i |
1.90754–0.8978 i |
1.9076–0.897 i |
|
3 |
2,75652–0,99151 |
2.75652–0.9915 i |
- |
|
4 |
3,63132–1,06662 i |
3.63132–1.0666 i |
- |
|
5 |
4.52440–1.13140i |
4.52440–1.1314 i |
- |
На основе приведенных исследованию выявлено, что рассматриваемая механическая система имеет дискретный комплексный собственный частоты.
В таблице 1 приведено сравнение численной результатов с другими авторами [2,3]. Полученные результаты показывают, что с увеличением модуля упругости соответствующие собственные частоты механической системы медленно увеличиваются.
Литература:
1. Сафаров И. И. Колебания и волны в диссипативно неоднородных средах и конструкциях.// Ташкент: Фан, 1992, -C. 250.
2. Pao Y. H., and Mow C. C., 1973, Diffraction of Elastic Waves of Dynamic stress concentrations, crane, Russakand Company, New York.
3. Baron. M.L., and Parnes A. T. 1961, “Diffraction of a Pressure Wave by a cylindrical Cavity in an Elastic medium” ASME Jourwal of ApplitedMechawics, Vol. 28, pp. 347–354.







