В данной статье рассматривается вопрос влияния высших гармоник тока на активное сопротивление цилиндрического провода в диапазоне частот от 50 до 2000 Гц. Выведена расчетная формула для активного сопротивления цилиндрического провода на произвольной частоте. Проанализированы закономерности изменения активного сопротивления медных и алюминиевых проводов в зависимости от частоты и площади поперечного сечения.
Ключевые слова: поверхностный эффект, несинусоидальность, активное сопротивления медного провода, активное сопротивление алюминиевого провода
This article has shown the problem of high-harmonics influence on cylindrical wire resistance according to the frequency range from 50 to 2000 Hz. Cylindrical wire resistance estimation for any frequency has been deduced.We have also analyzed cylindrical wire resistance dependence of copper and aluminum wires due to the frequency and cross section area.
Keywords: skin effect, high-harmonics, copper wire resistance, aluminum wire resistance
В Российской Федерации системы электроснабжения общего назначения работают на фиксированной частоте 50 Гц. Кроме основной гармоники, в сетях присутствуют также высшие гармоники токов и напряжений [1]. Исследования указывают на то, что при наличии в сети нелинейных нагрузок, наибольшим искажениям подвергается форма кривой тока, в то время как кривая напряжения практически не изменяется [5, 6]. Это объясняется тем, что реальные генераторы по своим свойствам близки к идеальным источникам ЭДС. Высшие гармоники тока приводят к дополнительному нагреву проводников линии электропередачи, в результате чего, с одной стороны возникают дополнительные потери мощности, с другой происходит ускоренный износ изоляции, изоляторов, растяжение проводов и другие негативные последствия [2]. По мере увеличения частоты, начинает проявляться поверхностный эффект, приводящий к перераспределению плотности тока в сечении проводника, от центра к поверхности, в результате изменяется его сопротивление, что в свою очередь влияет на потери мощности и энергии в линиях электропередачи электрической распределительной сети.
Задача данного исследования: определить степень изменения плотности тока в сечении провода и его сопротивления в зависимости от частоты гармоники тока протекающего по проводнику. Это позволит более точно рассчитать дополнительные потери мощности на нагрев проводов, обусловленные несинусоидальностью питающего напряжения электрической распределительной сети.
Провод можно приближенно представить в виде цилиндрического проводника, длина которого многократно превышает радиус. Для нахождения плотности тока используют уравнения Максвелла, решение которых производится в цилиндрической системе координат [3]. В результате выражения для плотности тока и напряженности магнитного поля в любой точке сечения цилиндрического проводника:
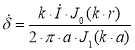 (1)
(1)
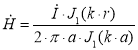 (2)
(2)
где ![]() — комплексная плотность тока, А/м2;
— комплексная плотность тока, А/м2; ![]() — напряженность магнитного поля, А/м;
— напряженность магнитного поля, А/м; ![]() — комплексный ток, А; J0 — функция Бесселя 1-го рода 0-го порядка; J1 — функция Бесселя 1-го рода 1-го порядка; r — радиус текущей поверхности тока в проводе, м; a — радиус провода, м;
— комплексный ток, А; J0 — функция Бесселя 1-го рода 0-го порядка; J1 — функция Бесселя 1-го рода 1-го порядка; r — радиус текущей поверхности тока в проводе, м; a — радиус провода, м; ![]() — комплексное волновое число, м-1;
— комплексное волновое число, м-1; ![]() — круговая частота, рад/с; f — циклическая частота, Гц;
— круговая частота, рад/с; f — циклическая частота, Гц; ![]() — абсолютная магнитная проницаемость, Гн/м; µ — относительная магнитная проницаемость; µ 0= 4·π·10–7 Гн/м — магнитная постоянная.
— абсолютная магнитная проницаемость, Гн/м; µ — относительная магнитная проницаемость; µ 0= 4·π·10–7 Гн/м — магнитная постоянная.
Формулы (1), (2) не учитывают «эффект близости», т. к. для этого необходимо точно знать пространственное расположение проводников. При расстоянии между проводами многократно превышающем радиус и невысоких значениях тока «эффектом близости» можно пренебречь.
Мощность рассеиваемую цилиндрическим проводом определяют по закону Джоуля-Ленца в комплексной форме:
![]() (3)
(3)
С другой стороны рассеиваемую мощность находим, используя теорему Умова-Пойнтинга [3]:
![]() (4)
(4)
Приравнивая выражения (3) и (4) получаем:
![]() (5)
(5)
В результате комплексное сопротивление выражаем формулой:
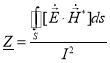 (6)
(6)
Вектор напряженности электрического поля ![]() вычисляем по формуле:
вычисляем по формуле:
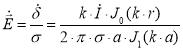 (7)
(7)
где σ — удельная проводимость, См/м.
Учитывая, что площадь боковой поверхности цилиндрического проводника равна S=2·π·a·lи радиус поверхности равен радиусу провода r=a получаем:
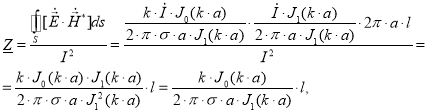
где l — длина проводника, м.
Таким образом, окончательное выражение для комплексного сопротивления цилиндрического провода приняло вид:
![]()
Активное сопротивление при этом определяем, как действительную часть полного комплексного сопротивления:
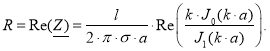 (8)
(8)
Рассчитаем сопротивления медных проводов и алюминиевых проводов марок А, АКП, АН, АНКП, АЖ, АЖКП. Сечения выберем самые распространенные: 16, 25, 35, 50, 70, 95, 120, 150, 185 мм2 [4], хотя каких-либо ограничений по сечению проводов нет. Единственное условие данного метода: длина должна быть много больше радиуса l>>a. Удельная проводимость меди σCu=56·106 См/м, а удельная проводимость алюминия σAl=37·106 См/м. Относительная магнитная проницаемость обоих материалов приблизительно равна µ=1 (медь является диамагнетиком, а алюминий парамагнетиком). Радиус провода выражаем из формулы площади круга:
![]() ,
,
где s — площадь сечения провода, мм2.
Расчета активного сопротивления медных проводов различных сечений, выполнен в диапазоне частот 0–2 кГц (рисунок 1.). Аналогичный расчет проведен для алюминиевых проводов (рисунок 2.). Выбор диапазона обосновывается тем, что согласно ГОСТ Р54149–2010, гармоники нормируются до 40-й включительно, что соответствует наибольшему значению частоты 2кГц [1].
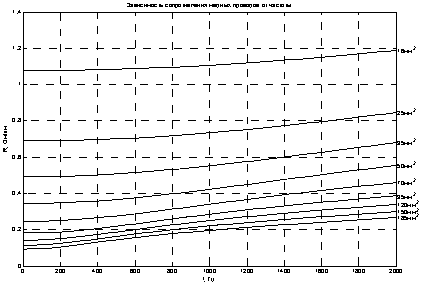
Рис. 1. Зависимость активного сопротивления медных проводов различных сечений от частоты
Семейства графиков (рисунки 1, 2) показывает зависимость погонного сопротивления проводов как от их сечения, так и от частоты. В полосе частот от 0 до 2000 Гц (рисунок 1.) величина возрастания сопротивления от 10,4 % до 183,9 %, в зависимости от сечения провода. Причем наибольший, в процентном отношении, прирост сопротивления наблюдается на больших сечениях. Например, при сечении 16 мм2 погонное сопротивление увеличивается с 1,08 до 1,19 Ом/км, что составляет 10,4 %, а при наибольшем сечении 185 мм2 погонное сопротивление увеличивается с 0,09 до 0,27 Ом/км, что в пересчете на проценты составляет 183,9 %. Это объясняется большей неравномерностью плотности тока при большем радиусе сечений проводов.
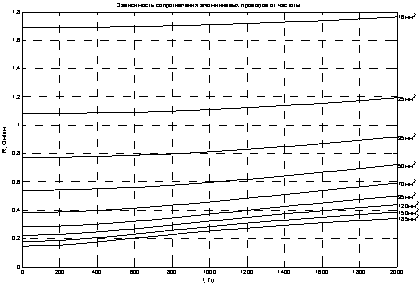
Рис. 2. Зависимость активного сопротивления алюминиевых проводов различных сечений от частоты
Результаты, полученные для алюминиевых проводов (рисунок 2.), аналогичны результатам для медных проводов. Сопротивление возрастает на величину от 4,4 % до 133,8 %, в зависимости от сечения провода, наименьший прирост погонного сопротивления наблюдается при сечении 16 мм2, в этом случае погонное сопротивление увеличивается с 1,69 до 1,76 Ом/км, что составляет 4,4 %, а при наибольшем приведенном на графике сечении 185 мм2 погонное сопротивление увеличивается с 0,15 до 0, 34 Ом/км, что в пересчете на проценты составляет 133,8 %.
Таким образом для проводников большего сечения поверхностный эффект оказывает более выраженное влияние на сопротивление (для меди сопротивление возросло на 183,9 %, а для алюминия на 133,8 %, в полосе частот от 0 до 2000 Гц), уменьшение же сечения приводит к существенному возрастанию активного сопротивления (рисунки 1,2.). Проводники с большей удельной проводимостью более подвержены влиянию поверхностного эффекта. При равном сечении, по мере увеличения частоты, активное сопротивление медного провода возрастает быстрее, чем активное сопротивление алюминиевого провода.
Литература:
- ГОСТ 32144–2013 Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. [Текст] — М.: Стандартинформ — 2014г. — 38 с.
- Григорьев О. Высшие гармоники в сетях электроснабжения 0,4 кВ/ О. Григорьев, В. Петухов, В. Соколов, И. Красилов [Текст] //«Новости электротехники», № 6(18) 2002–1(19) 2003.
- Бессонов Л. А. Теоретические основы электротехники [Текст] — М.: Высшая школа — 1964г. — 750 с.
- Будзко И. А. Элетроснабжение сельского хозяйства/ И. А. Будзко, Т. Б. Лещинская, В. И. Сукманов [Текст] — М: Колос — 2000 г. — 536 с.
- Бессонов Л. А. Линейные электрические цепи / Л. А. Бессонов. — М: Высшая школа, 1983. — 336 с.
- Лосев А. К. Теория Линейных электрических цепей / А. К. Лосев. — М: Высшая школа, 1987. — 512 с.







