Для линейного оператора 
в гильбертовом пространстве 
с областью определения 
множество 
называется его числовым образом. Известно, что точечный спектр 
оператора 
лежит в 
, а его аппроксимативно точечный спектр 
содержится в 
, см. например [1].
Для того, чтобы получить более точную информацию о спектре, в работе [2] введено понятие квадратичный числовой образ, затем изучена в работе [3]. Это множество определено, если дано разложение 
и 
, где 
и 
гильбертово пространство, а 
пространство линейных ограниченных операторов в гильбертовом пространстве 
. Тогда оператор 
всегда записывается в виде блочно–операторной матрицы
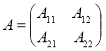(1)
с линейными ограниченными операторами 
, 
.
Для полноты дадим определение квадратичной численной области значений оператора 
. Пусть 
и 
–скалярное произведение и норма в 
, 
, соответственно. Множество всех собственных значений матрицы
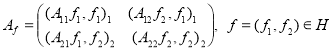
таких, что 
, 
называется квадратичной числовой образ оператора 
, соответствующей представлению (1) блочно-операторной матрицы 
и обозначается как 
, т. е. 
.
Пусть теперь дано прямая сумма 
трех гильбертовых пространствах , 
и 
, а также оператор 
. Тогда оператор 
всегда записывается в виде блочно–операторной матрицы
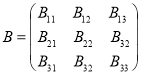(2)
с линейными ограниченными операторами
, 
.
Множество всех собственных значений матрицы
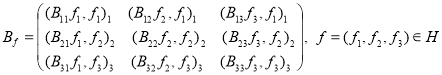
таких, что , 
называется кубической числовой образ оператора 
, соответствующей представлению (2) блочно-операторной матрицы 
и обозначается как 
, т. е. 
.
Для двум различным разложениям гильбертово пространства 
, могут соответствовать различные кубические числовые образы. Приведем некоторые факты и примеры. Заметим, что кубическая числовая образ всегда содержится в числовом образе: 
. При этом если операторная матрица 
имеет нижнюю или верхнюю треугольную форму, т. е.
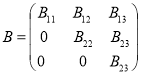или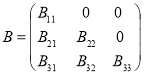 
,
то 
.
Аналогично числового образа значений, кубическый числовой образ ограниченной блочно-операторной матрицы 
является ограниченным подмножеством множество 
: 
и оно замкнуто если 
.
Пример 1. Кубический числовой образ матрицы 
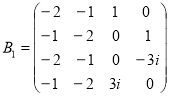
соответствующий разложений 
имеет вид:
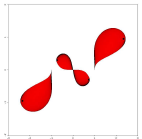
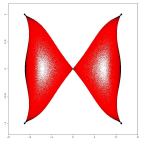
Пример 2. Кубический числовой образ матрицы
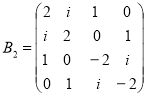
соответствующий разложений 
имеет вид:
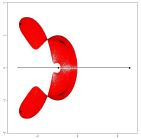
Пример 3. Кубический числовой образ матрицы
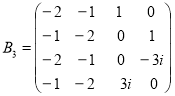
соответствующий разложений 
имеет вид:
Пример 4. Кубический числовой образ матрицы
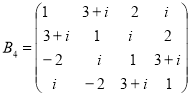
соответствующий разложений
имеет вид:
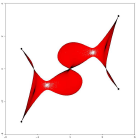
Литература:
- Т. Като. Теория возмущения линейных операторов. М.: Мир, 1972.
- H. Langer, C. Tretter. Spectraldecomposition of some nonselfadjoint block operator matrices. J. Operator Theory, 39:2 (1998), 339–359.
- H. Langer, A. S. Markus, V. I. Matsaev, C. Tretter. A new concept for block operator matrices: the quadratic numerical range. Linear Algebra Appl., 330:1–3 (2001), 89–112.
