В данной статье исследованы математические модели построения метеопрогноза, основанные на работе нейронных сетей, которые позволяют вычислить предположительные метеопараметры искомой местности на основе предыдущих метеоданных. Предложен новый метод группировки нейронных сетей для получения более точного результата на выходе. Представлен алгоритм, опираясь на который, исходя из результатов исследования, был получен наиболее точный метеопрогноз. Данный алгоритм может быть использован в широком спектре ситуаций, таких как: получение данных для эксплуатации оборудования в данной локации, исследование метеорологических параметров локации и т. п.
Для построения данной модели были использованы данные полученные с персональных погодных станций (ППС) компании WeatherUndergroundи Национальной Цифровой Метеопрогнозной Базы Данных США (USNationalDigitalForecastDatabase (NDFD)). А также, для сравнения результатов с уже имеющимися на рынке продуктами, была использована удаленная обучающаяся машина компании Google.
Алгоритм построения прогнозной модели затрагивает несколько локаций расположенных на территории США для сравнения эффективности в различных погодных зонах. А также были рассмотрены разные методы обучения машины для получения самого эффективного результата метеопрогноза.
Одной из самых распространенных проблемой обеспечения научной, производственной и других деятельностей человека была и остается проблема своевременного получения информации об окружающей среде в необходимый момент времени. Особенно важной данная проблема становится для поддержки технических систем (ТС), зависимых от метеоусловий, и работающих в автономном режиме. Их параметры не могут быть откалиброваны в зависимости от метеоусловий на данный момент, что ставит перед создателями таких систем необходимость решения проблемы предсказания метеоусловий на продолжительном отрезке времени. В то время как предсказание значений для однопараметрических технических систем (ОТС) не представляет особых проблем, МТС требует вдумчивого подхода к созданию алгоритма построения прогнозной модели, что делает данную проблему весьма актуальной.
На данный момент известны различные методы и средства получения и прогнозирования метеоданных на искомой локации (её параметрах), таких как:
- Исследование погодных явлений на текущей локации при помощи физических законов. (WeatherResearch&ForecastingModelhttp://www.wrf-model.org)
- Исследование погодных условий при помощи математических преобразований данных полученных с Зондов.
Целью данногоисследования является описание и анализ алгоритма построения прогнозной модели для МТС для конкретной местности на примере данных полученных с ППС для определенных регионов при помощи самообучающихся машин, а так же их сравнение.
Современное количество решений проблемы построения метеопрогнозных моделей и их анализа поражают. Одним из самых успешных, но в то же время, самых затратных решений является решение предоставленное WeatherResearch&Forecasting, которое сводится к построению математической модели физических явлений и применение на текущих данных определённой локации, однако такой подход редко даёт точный результат, так как требует огромных ресурсов для решения и требует постоянного расчёта с учётом меняющихся параметров системы, а также требует таких-же построений моделей для соседних регионов, что увеличивает расходы на точный прогноз экспоненциально, а также не учитывает колебания вызванные многими параметрами, которые не могут зафиксировать зонды.
Нейронные сети используют один из наиболее перспективных методов прогнозирования МТС, которым является математическая экстраполяция, так как этот метод основывается только на статистическом анализе данных. Минусом же данного подхода является невозможность экстраполировать развитие процесса вперед на длительный временной интервал, для этого они строят закономерности между входными и выходными значениями, опираясь на обучающие данные, в случае с метеопрогнозом такими данными являются предыдущие наблюдения, собранные ППС.
В данной работе используется обучающая парадигма, в которой конечное количество нейронных сетей обучаются по одинаковым данным для получения искомого результата, такая парадигма называется группировкой нейронных сетей.
1.Описание и применение нейронных сетей.
1.1 Описание математической модели D-PNN
Рассмотрим математическую модель построения метеопрогноза использующую самообучающуюся машину, основанную на решении дифференциального многочлена (DifferentialpolynomialneuralnetworkD-PNN). D-PNN описывает функциональные зависимости входных параметров и исследование их свойств, которые часто используют для прогноза, анализа временных рядов и выявления скрытых взаимосвязях в данных [1]. Того удаётся достичь путём шаблонизирования зависимостей между данными. Главной идеей D-PNN является аппроксимация функций, описываемых дифференциальными уравнениями, которые описывают взаимосвязи между входными параметрами системы. Связи между данными описываются аналогично, представленному в 1971 году, многочлену Колмогорова-Габора [2]:
![]() , (1)
, (1)
где: m-кол-во переменных, ![]() - вектора входных переменных,
- вектора входных переменных,
![]() - вектора параметров.
- вектора параметров.
Данный многочлен можно разбить на более простой многочлен применимый к каждой паре входных значений:
![]() , (2)
, (2)
Данный подход строит многочленную комбинацию входных данных. (Group Method of Data Handling GMDH)
D-PNN подход состоит в аппроксимации полученных зависимостей во входных данных.
![]() , (3)
, (3)
где: ![]() - функциональные зависимости входных данных,
- функциональные зависимости входных данных, ![]() - параметры
- параметры
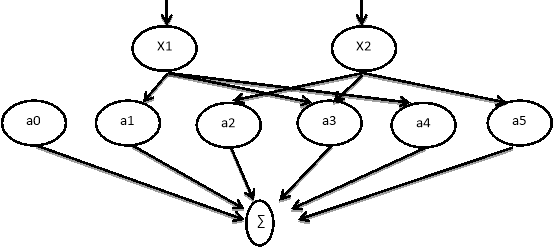
Рис. 1: Многочленный нейрон GMDH
Элементарные методы общего решения дифференциального уравнения — выразить решение в специальных элементарных функциях — полиномах (таких как степенные ряды). Численное интегрирование дифференциальных уравнений основано на аппроксимации их с помощью интегральных функций. В данной работе я использовал метод интегральных аналогий, путём замены математических операторов в уравнении с отношением соответствующих значений.
![]() , (4)
, (4)
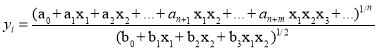 , (5)
, (5)
где: n — степень n входных значений числителя, m- степень знаменателя (m
Полиномы 4 описывают частичную зависимость n входных значений от каждого нейрона и применяются в дифференциальном уравнении 3. Они создают многопараметрическую нелинейную функцию, которая описывает зависимость переменных. Числитель уравнения 4 это полином полных n-входных комбинаций одного нейрона и используется как функция z в формуле 6. Знаменатель же является производной, которая даёт частичное взаимное изменение входных переменных определенного нейрона. (m
где: z — функция n входных параметров,
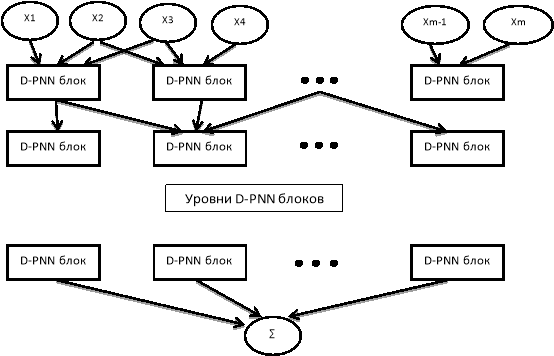
Рис. 2: Схема D-PNN
1.2. Описание математической модели RBFN
RadialBasisFunctionNetwork (RBFN) использует абсолютно иной подход в построении математической модели, предсказывающей будущие значения [4]. Данная нейронная сеть использует радиально-базисные функции как активационные, общий вид которых представляет собой:
где: x — вектор входных сигналов нейрона,
RFBN очень популярна для аппроксимации функций, предсказаний ременных рядов и классификаций. В таких сетях очень важно определить количество нейронов в скрытом слое (hiddenlayer), так как это сильно влияет на сложность сети и её обобщающие возможности [5]. В скрытом слое каждый нейрон имеет активирующую функцию. Гауссова функция, которая имеет параметр управляющий поведением функции, является наиболее предпочтительной функцией активации.
где: a,b,c — вещественные числа.
Обучение RBFN также включает в себя оптимизацию параметров каждого нейрона, затем весовые коэффициенты между скрытым и выходным слоями должны быть выбраны соответствующим образом и наконец, смещения, которые добавляются с каждым выходом, определяются на этапе обучения модели. Такая сеть состоит из трёх слоёв: входной слой, скрытый слой и выходной слой, при этом скрытый уровень представляет собой Радиально-базисные функции.
![]()
![]() (6)
(6)
![]() — весовой коэффициент
— весовой коэффициент
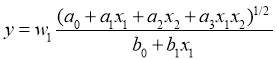 (7)
(7)
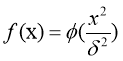 (8)
(8)
![]() - ширина окна функции,
- ширина окна функции, ![]() - убывающая функция (чаще всего, равная нулю вне некоторого отрезка).
- убывающая функция (чаще всего, равная нулю вне некоторого отрезка).
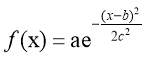 (9)
(9)
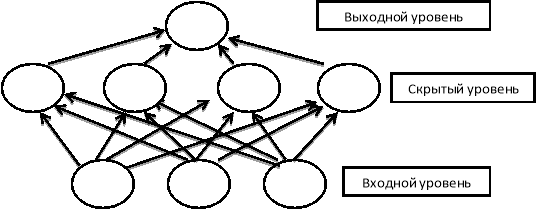
RBFN с m выходами можно выразить как:
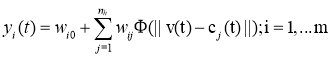 (10)
(10)
где: ![]() - весовой коэффициент для i-го блока в j-й выход.
- весовой коэффициент для i-го блока в j-й выход.
В данной работе использовалось дополнительные линейные соединения, позволяющие входным значениям соединяться напрямую к выходному узлу образуя линейную модель параллельно с не линейным стандартом RBF модели. Такой подход был придуман Годсом и Калантаром в 2010 году. Новую RBFN с m выходами, n входами и n1 линейными входными соединениями можно описать:
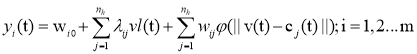 (11)
(11)
где: ![]() и vl — весовой коэффициент и входной вектор для линейных соединений, который может состоять из предыдущих входных и выходных параметров. Количество необходимых линейных соединений, как правило, гораздо меньше, чем число скрытых узлов в сети RBF.
и vl — весовой коэффициент и входной вектор для линейных соединений, который может состоять из предыдущих входных и выходных параметров. Количество необходимых линейных соединений, как правило, гораздо меньше, чем число скрытых узлов в сети RBF.
1.3 Описание математической модели MLPN
Самой распространенной нейронной сетью является Многослойныйперцептрон (Multilayerperceptron MLP). Этот тип известен тем, что требует наличие желаемого результата в массиве обучающих данных, в нашем случае, необходимо подавать дополнительное значение, которое будет являться правильным результатом для входных данных [6]. Иными словами, данная модель связывает входные значения с их результатом, используя исторические данные погоды, для предсказания в будущем.
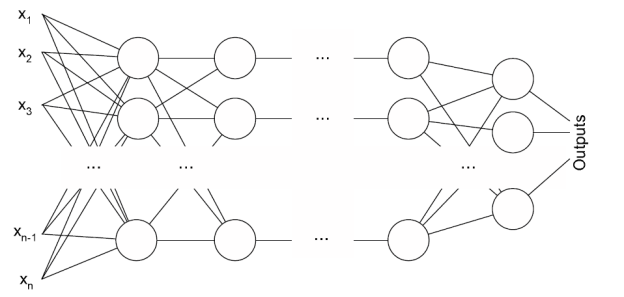
Рис. 4: Схема многослойного перцептрона
Такая сеть имеет простую интерпретацию в форме вход-выход модели с весовыми и пороговыми значениями свободных параметров. Такие сети могут моделировать функции почти произвольной сложности. Важной особенностью MLP является количество скрытых слоев и количества узлов на этих слоях. Как только количество слоёв и узлов определено нужно установить весовые коэффициенты и пороговые значения так, чтобы минимизировать погрешности при прогнозе. Эту роль берёт на себя обучающий алгоритм, называемый алгоритмом обратного распространения ошибки. Современные алгоритмы, например алгоритм Левенберга-Маркуарда, заметно быстрее выбранного, однако выбранный алгоритм обладает большей надежностью и прост для понимания и реализации.
Суть обратного распространения ошибок состоит в распространении сигналов ошибки от выходов сети к её входам, в направлении, обратном обычной работе сети [7]. Пусть имеется сеть с множеством входов ![]() , множеством выходов Outputs и множеством узлов, тогда обозначим весовой коэффициент
, множеством выходов Outputs и множеством узлов, тогда обозначим весовой коэффициент![]() стоящий на ребре i-й и j-й узлы, а через
стоящий на ребре i-й и j-й узлы, а через ![]() выход i-го узла, тогда если нам известен правильный ответ
выход i-го узла, тогда если нам известен правильный ответ ![]() для обучающего набора данных, то функция ошибки, полученная при использовании метода наименьших квадратов, выглядит так [8]:
для обучающего набора данных, то функция ошибки, полученная при использовании метода наименьших квадратов, выглядит так [8]:
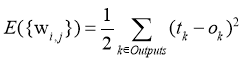 (12)
(12)
Затем подправляются весовые коэффициенты после каждого обучающего примера и, таким образом, они «двигаются» в многомерном пространстве весов. Чтобы добиться минимума ошибки нужно «двигаться» в сторону противоположную градиенту, иными словами, на основании каждой группы правильных ответов, добавлять к каждому весовому коэффициенту ![]() , таким образом получаем:
, таким образом получаем:
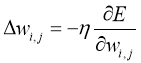 (13)
(13)
где 0<![]() <1 — множитель, задающий скорость «движения»
<1 — множитель, задающий скорость «движения»
Производная считается следующим образом. Пусть интересующий нас весовой коэффициент входит в нейрон последнего уровня (![]() ), тогда
), тогда ![]() - сумма весового коэффициента для входа j-го узла. Так как
- сумма весового коэффициента для входа j-го узла. Так как ![]() влияет на выход сети только как часть этой суммы, то:
влияет на выход сети только как часть этой суммы, то:
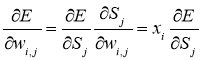 (14)
(14)
![]() аналогично влияет только на общую ошибку в рамках выхода j-го узла. Поэтому:
аналогично влияет только на общую ошибку в рамках выхода j-го узла. Поэтому:
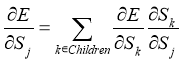 (15)
(15)
где Children — выходы узла, расположенного не на последнем уровне.
Ну а
1.4. Описание математической модели группировки нейронных сетей
Группировка нейронных сетей — это подход к построению самообучающейся машины, в которой совокупность конечного числа нейронных сетей обучается по одной и той же задаче. Этот подход берёт своё начало от Хансена и Саламона [9] в работе, которой показывает, что система нейронных сетей может существенно улучшиться при подходе группировки, а это значит, что и предсказания которые производит такая машина намного точнее. В целом, группировку нейронных сетей можно разделить на два этапа: обучение нескольких нейронных сетей и затем объединение и обработка предсказаний каждой. Результатом работы такой системы является усредненное значение выводов каждой нейронной сети в отдельности, объединенное с функцией, описывающей сравнительное отклонение значений относительно друг друга, полученное на этапе обучения. Результаты работы таких систем существенно повышают точность прогнозов.
В данной работе будет рассмотрен новый подход для обучения данных систем. Весовые коэффициенты пропорциональны соответствующим выходным значениям. Суть подхода в том, чтобы определить какая нейронная сеть выдаёт более точный прогноз. Рассмотрим на примере: предположим, что имеется две нейронные сети, которые должны выполнить простую классификационную задачу, если на вход подано значение 1, то выдать единицу, если 0, то выдать 0. Пусть такие нейронные сети на определённом шаге выдают 0,6 и 0,9 соответственно. В таком случае вторая машина получает намного более достоверные данные, так-как 0,9 ближе к единице.
Для начала рассмотрим некоторые прошлые исследования, связанные с группировкой нейронных сетей. Пусть имеем n сетей, обучающихся на некотором массиве данных ![]() и решающую задачу классификации.
и решающую задачу классификации.
1.4.1 “Наивный” классификатор
Пусть функция, возвращаемая i-той сетью ![]() . Если сеть обучается на вывод 0 или 1 для негативной или позитивной классификации, можно считать значение 0,5 проблематичным для определения класса. «Наивный» подход состоит в перекрестной валидации этого значения
. Если сеть обучается на вывод 0 или 1 для негативной или позитивной классификации, можно считать значение 0,5 проблематичным для определения класса. «Наивный» подход состоит в перекрестной валидации этого значения ![]() и выборе сети
и выборе сети ![]() , которая минимизирует среднеквадратичное отклонение на значении CV. Среднеквадратичное отклонение для каждой сети:
, которая минимизирует среднеквадратичное отклонение на значении CV. Среднеквадратичное отклонение для каждой сети:
![]()
![]() (13)
(13)
Данный подход выводит любое значение, содержащееся в других сетях [10]. Хотя этот метод очень производительный, точность такого подхода, по понятным причинам, очень мала.
1.4.2 Простой метод группировки
Одним из самых простых способом является объединение выводов сетей путём нахождение среднего значения между ними. Такой метод носит название Простой метод группировки (Basicensemblemethod BEM) и определяется как:
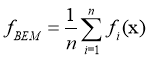 (14)
(14)
Такой подход ведёт к повышению производительность, однако не принимает в расчёт то, что некоторые сети могут быть более точными чем другие [10]. К плюсам этого метода также можно отнести простоту реализации.
1.4.3 Общий метод группировки
Обобщением для BEM метода заключается в нахождении весовых коэффициентов для каждого вывода, это минимизирует Среднеквадратичное отклонение группировки.
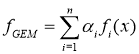 (15)
(15)
где: ![]() коэффициенты, которые выбираются для минимизации среднеквадратичного отклонения в отношении к применяемой функции. Пусть
коэффициенты, которые выбираются для минимизации среднеквадратичного отклонения в отношении к применяемой функции. Пусть ![]() ошибочное значение для сети
ошибочное значение для сети ![]() , такое что
, такое что![]() ,
, ![]() — корреляционная матрица, тогда нужно найти весовой коэффициент
— корреляционная матрица, тогда нужно найти весовой коэффициент ![]() , который минимизирует:
, который минимизирует:
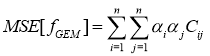 (16)
(16)
получаем:
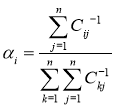 (17)
(17)
Такой метод обладает лучшей производительностью, чем BEM и даёт лучший результат, однако на практике такой метод очень часто содержит ошибки.
1.4.4 Методы динамической группировки
Если выход нейронной сети
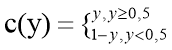 (18)
(18)
Вероятность принадлежности классу при y<0,5 растёт при уменьшении y, и наоборот при y![]() 0,5 при увеличении y. Можно сказать, что вывод сети
0,5 при увеличении y. Можно сказать, что вывод сети ![]() имеет меньшую вероятность попадания в класс относительно
имеет меньшую вероятность попадания в класс относительно ![]() , если
, если ![]() . Стоит учесть, что вероятности симметричны относительно позитивных и негативных предположений. Например, вероятность вывода 0,1 идентична вероятности при выводе 0,9 но при разных предположениях.
. Стоит учесть, что вероятности симметричны относительно позитивных и негативных предположений. Например, вероятность вывода 0,1 идентична вероятности при выводе 0,9 но при разных предположениях.
Если вместо выбора статических весовых коэффициентов, полученных из функций ![]() при единице входных данных использовать их в качестве регулировки c(y), то можно достичь большей производительности. Такой метод называется метод динамически усредненной сети (Dynamicallyaveragednetwork DAN) [12].
при единице входных данных использовать их в качестве регулировки c(y), то можно достичь большей производительности. Такой метод называется метод динамически усредненной сети (Dynamicallyaveragednetwork DAN) [12].
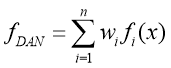 (19)
(19)
где ![]() :
:
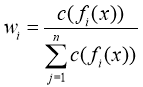 (20)
(20)
Сумма ![]() равна 1, поэтому
равна 1, поэтому ![]() это усредненный весовой коэффициент вывода сети. Разница заключается в том, что вектор весовых коэффициентов пересчитываются каждый раз при получении вывода сети вместо статически выбранного весового коэффициента, который даёт оптимальное решение в отношении поперечного набора данных. Вклад каждой сети в сумме пропорционален ее достоверности с(y). Например, значение близкое к 0,5 будет мало влиять на сумму, в отличии от таких значений как 0,99; 0,01. Этот метод очень схож с идеей использования соглашений между множества классификаторов, чтобы получить меру уверенности в решении, при этом каждый классификатор используется для получения окончательного решения. Каждая нейронная сеть, подключенная к группе, генерирует случайные весовые коэффициенты, затем каждая сеть обучается отдельно на предоставленных данных [13].
это усредненный весовой коэффициент вывода сети. Разница заключается в том, что вектор весовых коэффициентов пересчитываются каждый раз при получении вывода сети вместо статически выбранного весового коэффициента, который даёт оптимальное решение в отношении поперечного набора данных. Вклад каждой сети в сумме пропорционален ее достоверности с(y). Например, значение близкое к 0,5 будет мало влиять на сумму, в отличии от таких значений как 0,99; 0,01. Этот метод очень схож с идеей использования соглашений между множества классификаторов, чтобы получить меру уверенности в решении, при этом каждый классификатор используется для получения окончательного решения. Каждая нейронная сеть, подключенная к группе, генерирует случайные весовые коэффициенты, затем каждая сеть обучается отдельно на предоставленных данных [13].
1.4.5 Обзор предлагаемого алгоритма группировки нейронных сетей
Сети обратного распространения устанавливают начальные весовые коэффициенты случайным образом, чтобы уменьшить среднеквадратичное отклонение. Разница в начальных весовых коэффициентах даёт разные результаты. Таким образом, группировка нейронных сетей интегрируют эти независимые сети для улучшения обобщающей способности. Этот метода также гарантирует увеличение точности с точки зрения среднеквадратичного отклонения [14].
Рассмотрим одну нейронную сеть, которая обучается на некотором массиве данных. Пусть x — входной вектор, который появляется впервые в данной сети, а d — желаемый результат. x и d представляют реализацию случайного вектора X и случайной величины D соответственно. Пусть F(x) — функция ввода-вывода, реализованная с помощью сети. Тогда:
где: E [D|X=x] — математическое ожидание, ![]() - квадрат смещения:
- квадрат смещения:
![]() (22)
(22)
и ![]() - разница:
- разница:
![]() (23)
(23)
Ожидание ![]() по множеству D называется множеством, охватывающим распределение всех обучающих данных, таких как входные и выходные значения, и распределение всех начальных условий. Существует несколько способов индивидуального обучения нейронной сети и несколько способов группировки их выходных данных. В данной работе предполагается, что сети имеют одинаковые конфигурации, но начинают своё обучение с разных начальных условий. Для объединения выходных данных группы нейронных сетей используется усредненную простую группировку. Пусть
по множеству D называется множеством, охватывающим распределение всех обучающих данных, таких как входные и выходные значения, и распределение всех начальных условий. Существует несколько способов индивидуального обучения нейронной сети и несколько способов группировки их выходных данных. В данной работе предполагается, что сети имеют одинаковые конфигурации, но начинают своё обучение с разных начальных условий. Для объединения выходных данных группы нейронных сетей используется усредненную простую группировку. Пусть ![]() - множество всех начальных условий,
- множество всех начальных условий, ![]() - усредненное значение ввода-вывода функций сети. Тогда по аналогии с уравнением 21 получаем:
- усредненное значение ввода-вывода функций сети. Тогда по аналогии с уравнением 21 получаем:
![]() (24)
(24)
где ![]() — квадрат отклонения, определяемый множеством
— квадрат отклонения, определяемый множеством ![]() :
:
![]() (25)
(25)
и ![]() - соответствующая разница:
- соответствующая разница:
![]() (26)
(26)
Математическое ожидание
Из определения множества D можно представить его в качестве множества начальных условий ![]() и оставшееся множество обозначается через D’. По аналогии с уравнением 21 получаем:
и оставшееся множество обозначается через D’. По аналогии с уравнением 21 получаем:
![]() (27)
(27)
где ![]() - квадрат отклонения, определяемый множеством D’:
- квадрат отклонения, определяемый множеством D’:
![]() (28)
(28)
и ![]() - соответствующая разница:
- соответствующая разница:
![]() (29)
(29)
Из определения множеств D, ![]() , D’ очевидно, что:
, D’ очевидно, что:
![]() (30)
(30)
Из этого следует, что уравнение 28 может быть переписано в эквивалентной форме:
![]() (31)
(31)
Учитывая разницу
![]() (32)
(32)
или
![]() (33)
(33)
Стоит учесть, что среднеквадратичное значение функции F(x) на множестве D должно быть больше или равно среднеквадратичному значению функции ![]() на множестве D’.
на множестве D’.
![]() (34)
(34)
Учитывая уравнения 32 и 33:
![]() (35)
(35)
Отсюда, учитывая уравнения 31 и 35 можно сделать два вывода:
-
Смещение функции
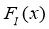 , относящееся к нескольким классифицирующим системам точно такое же, как смещение функции F(x) относящееся к одной нейронной сети.
, относящееся к нескольким классифицирующим системам точно такое же, как смещение функции F(x) относящееся к одной нейронной сети.
-
Разница функции
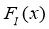 меньше чем функции F(x).
меньше чем функции F(x).
Группировка линейных нейронных сетей продемонстрировала повышение производительности по отношению к отдельным сетям. В данной работе представлена группировка нелинейных упреждающих сетей, порожденных конструктивным алгоритмом. Аналогичный подход был применён для, рассмотренных ранее, D-PNN, RBGN, MLP.
2. Обзор результатов работы рассмотренных математических моделей
Таким образом, входными параметрами будут исторические данные, полученные с ППС и результатом обучения будет функция зависимости этих параметров друг от друга, тогда при вводе достаточных данных в запросе на прогноз в будущем мы получим необходимые нам данные. Для построения прогноза на основе вышеупомянутых математических моделей нужно упорядочить полученные данные в виде массива перечисляемых параметров:
Таблица 1
Пример входных данных для обучения
|
Temp |
City |
Daytime |
Day_of_year |
Year |
Humidity% |
WindSpeedkph |
PressureinmBar |
WeatherConditions |
|
12.0 |
1 |
3 |
1 |
2001 |
14 |
5 |
1200 |
2 |
|
12.5 |
1 |
4 |
1 |
2001 |
15 |
4 |
1150 |
3 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
В данном случае, так как модель оперирует числовыми данными, городам и описанию погоды были выделены определённые индексы, например 1 в графе города означает Лос-Анджелес. В процессе исследования было проведено несколько способов обучения, путём манипуляции подаваемы значений.
Определим, как работают модели для разных сезонов, для этого подаём на вход данные за 5 лет и сравним полученные данные с реальными значениями за разные периоды (0:00–23:00 1-го января 2015, 0:00–23:00 1-го апреля 2015, 0:00–23:00 1-го июля 2015 и 0:00–23:00 1-го октября 2015).
Таблица 2
Средние отклонения прогнозных значений температуры
|
|
D-PNN |
RBFN |
MLPN |
Assemble |
|
Зима |
17 % |
14 % |
14 % |
12 % |
|
Весна |
15 % |
13 % |
12 % |
10 % |
|
Лето |
13 % |
15 % |
10 % |
8 % |
|
Осень |
13 % |
15 % |
11 % |
9 % |
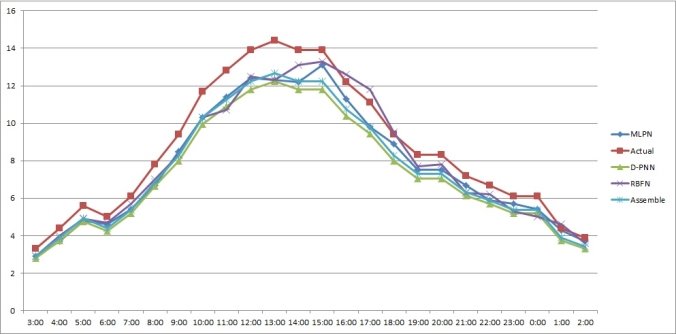
Рис. 5: График прогнозных значений, полученных каждым методом на 1-е января 2015 года
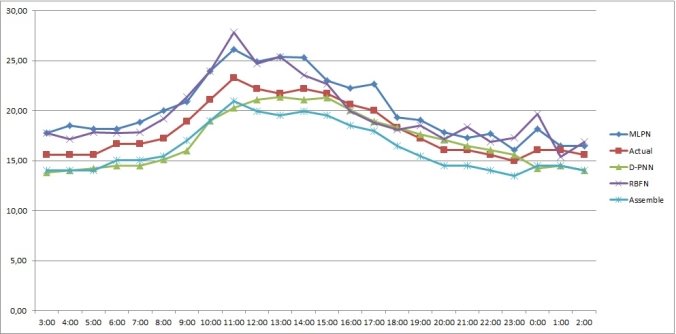
Рис. 6. График прогнозных значений, полученных каждым методом на 1-е апреля 2015 года
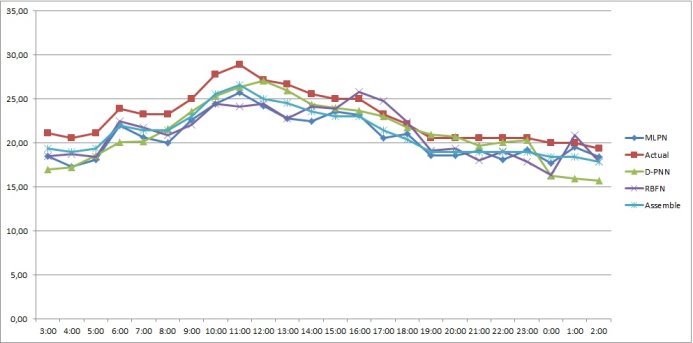
Рис. 7: График прогнозных значений, полученных каждым методом на 1-е июля 2015 года
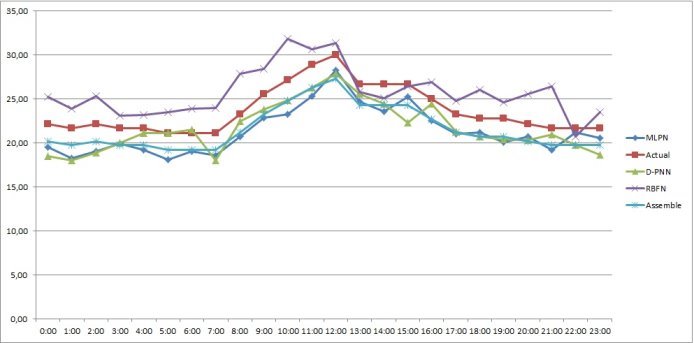
Рис. 8. График прогнозных значений, полученных каждым методом на 1-е октября 2015 года
Таким образом, созданный нами метод группировки нейронных сетей имеет лучшую точность во всех сезонах и имеет приемлемую точность ![]() 91 %.
91 %.
Заключение
В данной статье был разработан и исследован алгоритм построения метеопрогноза при помощи группировки нейронных сетей. Был рассмотрен алгоритм, построения математической модели предсказания будущих состояний параметров метеосистемы на основе Дифференциального многочлена, Радиально-базисных функций, Многослойного перцептрона и группировки нейронных сетей. Можно сделать вывод, что комбинация математических моделирования и «правильных» входных данных, связанных с погодными явлениями могут сделать метеопрогнозную модель более точной.
Автор данной статьи продолжает исследование моделей метеопрогноза путём усовершенствования не только порядка и точности входных данных, но и изменения математической основы построения самой модели.
Литература:
- Galkin I., Polynomial neural networks, 2000, стр. 307
- Zyavka L., Polynomia; neural network. Proceeding of the 7th European Conference Information and Communication Technologies, 2005, стр. 277–280.
- Obitko M., Generic algorithm, 2006, стр.205
- Paul J. and J. W. Sandberg, Universal approximation using RBFN, 1996, стр. 506–507
- Omania N., Improving the performance of back propagation, стр. 1343–1354
- Bishop C., Neural networks for pattern recognition, 1995, стр. 363–367
- Breiman L., Combining prediction, 1999, стр. 31–49
- Jiang Y, Rule learning based on neural network, 2002, стр. 1450–1453
- Krogh A., Vedelsky K., Neural network ensembles, 1995, стр 231–238
- Moro Q., Application of neural network to weather forecasting, 2004, стр. 68–70
- Rosen B., Ensemble learning using neural networks, 1997, стр. 372–383
- Zhou Z., Ensemble neural networks, 2003, стр. 239–263
- Zurada J., Introducing to artificial neural systems., 1993, стр. 283–291
- Luo. L, Application of radial basis function, 2010, стр. 97–117







