Принцип квазиэквивалентного укрупнения состояний марковских моделей



Использование математических моделей для проектирования сложных систем часто приводит к проблеме большой размерности пространства конструктивных параметров и сложности зависимостей между конструктивными и выходными параметрами. Аналитические марковские модели являются мощным и достаточно универсальным математическим аппаратом анализа характеристик сложных систем. Однако при их применении возникают известные проблемы размерности — рост пространства состояний модели и связей между состояниями при увеличении количества элементов анализируемой системы. В общем случае размерность пространства состояний марковской модели , где n — количество элементов системы, K_i — количество состояний, в которых может находиться i-й элемент системы. Если элемент может находиться в двух состояниях, работоспособном и неработоспособном, то размерность марковской модели будет 2ⁿ.

Укрупнение состояний марковской модели процесса может быть эквивалентным (точным) или квазиэквивалентным (приближенным). В теории марковских процессов рассматриваются условия, которым должна удовлетворять структура графа переходов для того, чтобы процесс допускал эквивалентное укрупнение. На практике же часто применяется именно квазиэквивалентное укрупнение.

Рис. 1. Структура модели

Проиллюстрируем применение методов эквивалентного и квазиэквивалентного укрупнения состояний графа переходов марковской модели. Рассмотрим модель, показанную на рис. 1, но с учетом возможных отказов и восстановления ЭВМ. Допустим, что интервалы безотказной работы и времена ремонта ЭВМ — независимые случайные величины, имеющие экспоненциальные распределения; их средние значения соответственно Т₀ = 1/α и Т_в = 1/β.

Состояние системы в момент времени t описывается вектором x(t) = (x1(t), x2(t)), где x1(t)ϵ{0, 1} — число неисправных ЭВМ; x2(t)ϵ{0, N} — число задач в очереди и ЭВМ. Граф переходов марковского процесса x(t) имеет структуру, показанную на рис. 2а. Для системы уравнений, соответствующей этому графу переходов, написать решение в явном виде не удается. Чтобы получить хотя бы приближенные алгебраические соотношения, связывающие выходные параметры с внутренними параметрами базисной модели, для предварительной прикидки, оценки вариантов, получения зависимостей качественного характера соотношения, проведем квазиэквивалентное укрупнение состояний графа переходов процесса x(t). Введём следующие обозначения: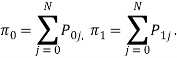

Рис. 2. Графы переходов марковского процесса: а) граф исходного процесса; б) граф процесса с эквивалентным укрупнением состояний; в) граф процесса с квазиэквивалентным укрупнением состояний

Запишем уравнения Колмогорова для стационарного распределения. Сложим уравнения, соответствующие состояниям верхнего ряда графа переходов, а затем уравнения, соответствующие состояниям нижнего ряда. В итоге имеем два уравнения относительно вероятностей π0 и π1, соответствующих укрупненному графу, изображенному на рис. 2б, полученному из исходного графа объединением в макросостояния состояний верхнего и нижнего ряда. В данном случае укрупнение состояний является эквивалентным, так как оно соответствует эквивалентному преобразованию исходной системы уравнений относительно стационарных вероятностей.

Укрупнённый граф позволяет легко найти коэффициент готовности системы (среднюю долю времени, соответствующую исправному состоянию):

Чтобы вывести простые формулы для , можно попытаться укрупнить граф «по вертикали», объединив состояния каждого столбца. Обозначим . Однако, если сложить соответствующие уравнения Колмогорова для исходного графа, обнаружим, что записанные уравнения, кроме стационарных вероятностей макросостояний , содержат вероятности исходных состояний :

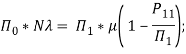
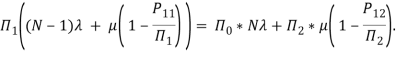
Таким образом, укрупнения достичь не удалось. Укрупненный граф можно получить при следующем допущении: . Однако данные соотношения выполняются лишь приближенно, поэтому укрупнение графа является квазиэквивалентным. В результате получается система уравнений, соответствующая укрупненному графу, изображенному на рис. 2в.

Для рассматриваемой модели квазиэквивалентное укрупнение состояний графа соответствует замене исходной модели системы с ненадежной ЭВМ системой с абсолютно надежной ЭВМ, имеющей производительность , то есть сниженную с до .

Рассмотрим изложенную выше процедуру квазиэквивалентного укрупнения на примере модели двухпроцессорной системы с отказами и восстановлением процессоров. Структура системы представлена на рис. 3.

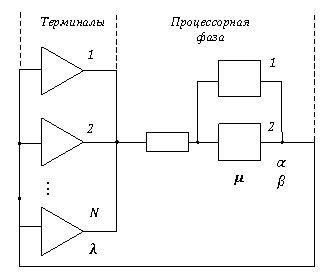
Рис. 3. Структура модели двухпроцессорной системы c отказами/восстановлением

В модели имеется N терминалов и 2 процессора. Как и в случае с однопроцессорной моделью, допустим, что интервалы безотказной работы и времена ремонта процессоров — независимые случайные величины, имеющие экспоненциальные распределения, их средние значения, соответственно, Т₀ = 1/α и Т_в = 1/β.

Состояние системы в момент времени t описывается вектором где число неисправных процессоров в момент , где число задач в момент , обрабатываемых в процессорах или ожидающих в очереди начала обработки.

При введенных допущениях о распределениях случайных величин, вызывающих изменения состояния системы вектор представляет собой марковский процесс. Исходный граф переходов этого процесса имеет структуру, показанную на рис. 4а, а на рис. 4б и 4в изображены графы переходов макросостояний, полученных в результате объединения в группы состояний исходного марковского процесса.

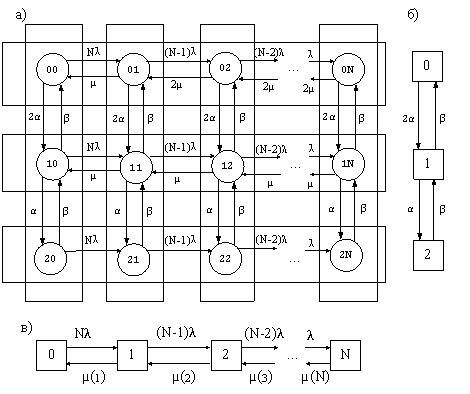
Рис. 4. Графы переходов для двухпроцессорной системы: а) граф исходного процесса; б) граф процесса с эквивалентным укрупнением состояний; в) граф процесса с квазиэквивалентным укрупнением состояний

Запишем уравнения Колмогорова, соответствующие стационарному режиму (производные в левой части уравнений равны нулю), для всех состояний исходного процесса.

Сложим уравнения для состояний верхнего ряда, сократим члены, входящие в правую часть уравнений с разными знаками, и вынесем общие множители за скобки. В результате получим уравнение , где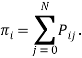

При внимательном рассмотрении структуры графа исходного процесса (рис. 4а) становится ясно, что если что если сложить уравнения, записанные для состояний верхнего ряда, то в них сократятся члены с интенсивностями перехода, соответствующими горизонтальным дугам, потому что они в одно уравнение входят со знаком плюс, а в другое уравнение из этой же группы со знаком минус. Остаются только члены с интенсивностями перехода, соответствующими вертикальным дугам, а эти интенсивности одинаковы для всех состояний горизонтального ряда, поэтому они выносятся за скобки. Из этого следует, что уравнение можно записать непосредственно из структуры графа исходного процесса. В это уравнение входят только вероятности макросостояний (групп состояний, имеющих одинаковый первый индекс — число неисправных процессоров).

Совершенно аналогично записываются уравнения для макросостояний среднего и нижнего ряда. Итого, имеем СЛАУ 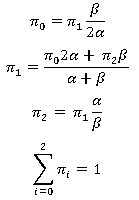(1):

(1)

Сопоставляя представленные выше уравнения со структурой графа на рис. 4б, видно, что они полностью соответствуют друг другу. Таким образом, укрупнение состояний исходного графа «по горизонтали», то есть объединение состояний с одинаковым первым индексом (числом неисправных процессоров), получилось эквивалентным. Эквивалентность означает, что если решить СЛАУ для вероятностей стационарных состояний исходного графа и потом сложить вероятности состояний с одинаковым первым индексом, то получится тот же результат, как при решении СЛАУ для графа на рис. 4б, которое записывается в явном виде просто по формулам для процесса размножения-гибели.

Попытаемся проделать аналогичную процедуру с группами уравнений «по вертикали», объединив в макросостояния состояния с одинаковым вторым индексом (числом задач в процессорной фазе). Обозначим при этом 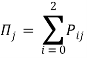, где .

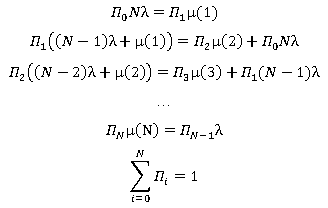(2)

Принимая во внимание допущение , имеем:

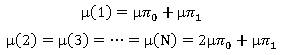(3)

Возьмём N=5, α=0,001, β=0,01, λ=0,1, μ=0,2. С учётом (3) СЛАУ (2) примет следующий вид:

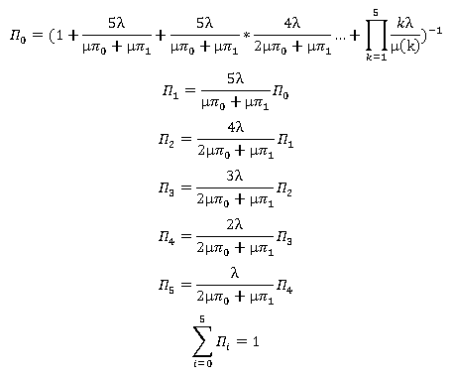(4)

Рассчитаем с учётом допущения :

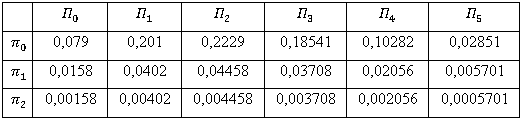(5)

Определим выходные параметры:

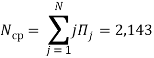— среднее число заявок в системе «процессоры-каналы»,

— среднее время реакции системы

Проверим правильность проведённых расчётов при помощи таблицы Excel (рис. 5):

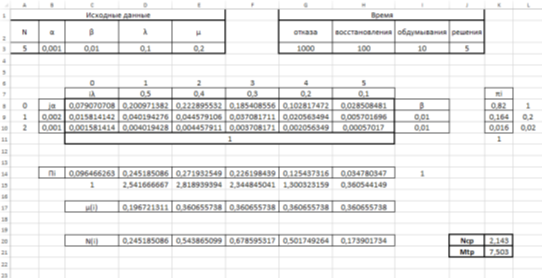
Рис. 5. Метод квазиэквивалентного укрупнения состояний

Исследуем, как ведут себя N_ср и M [t_р] при изменении исходных данных λ и μ и построим соответствующие графики зависимости (рис. 6):

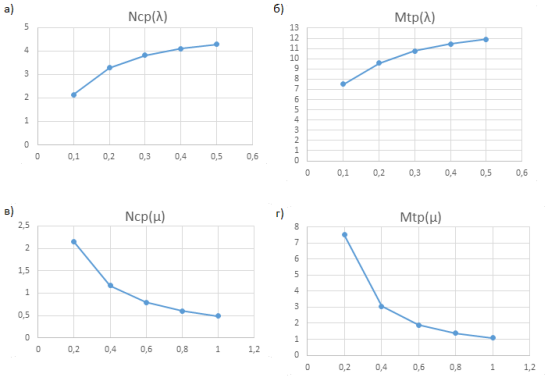
Рис. 6. Графики зависимости: а) N_ср(λ); б) M [t_р](λ); в) N_ср(μ); г) M [t_р](μ)

Как видим, значения выходных данных N_ср и M [t_р] растут увеличением λ и уменьшаются с ростом μ., следовательно, их поведение можно описать как закономерное. Это означает, что метод квазиэквивалентного укрупнения имеет право на существование и заслуживает более детального изучения. В дальнейшем будет исследована методическая погрешность данного метода и её влияние на итоговый результат работы АИС.

Литература:

1. Шкатов П. Н. Стохастические модели в анализе информационно-вычислительных систем. Учебное пособие
2. Г. Н. Церцвадзе, «Асимптотическое укрупнение состояний марковских цепей. I. Принцип стационарности потоков вероятностей», Автомат. и телемех., 1974, № 8, 31–38
3. http://lektsiopedia.org/lek-46079.html
4. http://lektsii.net/1–26000.html