Очевидно, что любой прямоугольник вида 4mx 4n разбивается на Т-тетрамино (см. рис.1). Пример такого разбиения при m=2, n=3 представлен на рис. 2.
![]()
Рис. 1. Т-тетрамино

Рис. 2. Разбиение 8х12 на Т-тетрамино
Кроме того, D. W. Walkup доказал, что только прямоугольники вида 4mx 4n разбиваются на Т-тетрамино. (см. [1])
Изучим структуру разбиений таких прямоугольников на Т-тетрамино.
Определение. Назовем сеткой m xn плоский граф G, множество вершин которого равно {1,…,m}x{1,…,n}, а ребрами соединены те вершины (i, j), (i`, j`), у которых |i — i`|+|j — j`|=1. На рисунке 3 приведен пример сетки 4х6. На рис. 4 — один из возможных способов разбиения сетки на простые циклы.
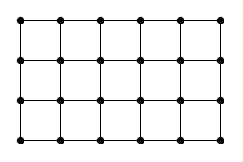
Рис. 3. Сетка 4х6
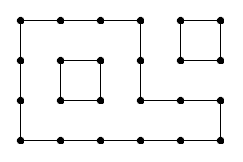
Рис. 4. Разбиение сетки 4х6 на простые циклы
Сопоставим разбиения прямоугольников 4mx 4n на Т-тетрамино и разбиения сеток 2mx 2n на простые циклы.
Разобьём прямоугольник 4mx 4n на квадраты 2 x 2. На центрах этих квадратов построим сетку, размер которой будет 2mx 2n со стороной 2 клетки. Сетка прямоугольника с m=2, n=3 (см. рис. 2) изображена на рис. 3. Заметим, что разбиение этой сетки на рис. 4 можно соотнести с разбиением прямоугольника 8х12 на Т-тетрамино на рис.2. Наглядное сопоставление приведено на рис. 5.

Рис. 5. Сопоставление разбиения прямоугольника 8х12 на Т-тетрамино и разбиения сетки 4х6 на простые циклы
Определение. Цикл разбивает плоскость на две области: конечную и бесконечную. Назовём конечную — внутренней областью, а бесконечную — внешней областью цикла.
Направим одно ребро цикла в любую сторону.Направление остальных рёбер определим по следующему принципу: два соседних ребра направим в одну сторону (то есть из их общей вершины одно ребро выходит, другое входит). Тем самым, если идти по направлению цикла, то можно вернуться в ту же вершину.
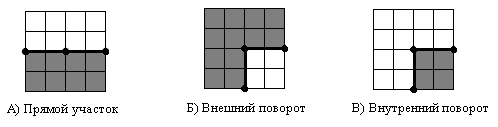
Рис. 6.
Определение. Рассмотрим два последовательных ребра цикла. Достроим квадрат 4 х 4 клетки так, чтобы в его центре была общая вершина этих рёбер (считаем, что ребро цикла имеет длину 2 клетки). Далее рассмотрим внутренние и внешние клетки цикла, принадлежащие квадрату. Если отношение внутренних к внешним 1:3, назовём совокупность этих двух рёбер внешним поворотом, если 3:1 — внутренним поворотом, если 1:1 — прямым участком. Объединение прямых участков будем так же считать прямым участком. Вершиной поворотаназовем общую вершину рёбер поворота. Иллюстрация к определениям приведена на рис. 6, где серым обозначена внутренняя область цикла.
Определение. Назовём двуповоротом два поворота, вершины которых соединены прямым участком, который в свою очередь назовём прямым участком двуповорота, а количество рёбер, принадлежащих прямому участку — длиной двуповорота. Выделим два вида двуповоротов: косой, один поворот которого внешний, другой внутренний, и прямой, у которого либо оба внутренних, либо внешних поворота. Косой двуповорот назовем хорошим (здесь и далее — по отношению к Т-тетрамино), если его длина кратна 2. Прямой двуповорот назовем хорошим, если его длина не кратна 2. Назовём циклхорошим, если все двуповороты в нём хорошие. На рис. 7 А) показан хороший прямой двуповорот длины 3, на рис. 7 Б) — хороший косой двуповорот длины 2.

Рис. 7.
![]()
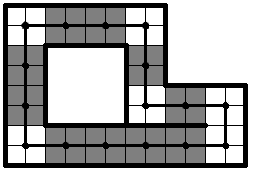
Определение. Назовём трубой множество клеток, хотя бы одна вершина которых принадлежит циклу, а границей трубы — множество всех границ клеток трубы, которые не касаются цикла. Граничная клетка трубы — клетка, одна из границ которой принадлежит границе трубы. Доминошкой двуповорота назовём множество из двух соседних граничных клеток, общая граница которых принадлежит прямому участку двуповорота.Прямым участком трубы назовём объединение доминошек одного из двуповоротов. Последняя доминошка двуповорота— доминошка двуповорота, которая является последней доминошкой двуповорота по направлению цикла. На рис. 8 приведен пример трубы, на котором жирным выделена её граница, а серым обозначены прямые участки её двуповоротов.
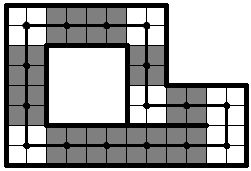
Рис. 8.
Будем говорить, что двуповорот можно разбить на Т-тетрамино, если существует цикл, сожержащий данный двуповорот, труба которого разбивается на Т-тетрамино.
Определение.Хорошей трубой назовём трубу, образованную хорошим циклом. Наконец, последнюю доминошку двуповорота будем называть хорошей, когда данный двуповорот можно разбить на Т-тетрамино.
Замечание 1. Рассмотрим разбиение прямого участка трубы на Т-тетрамино. Заметим, что доминошки можно разбить на 4 группы, в которых идентичным образом будут состыковываться Т-тетрамино. А каждая четвертая доминошка трубы будет принадлежать одной группе. (см. рис. 9)

Рис. 9. Доминошки
Расположим на плоскости поворот так, как показано на рис. 10 (стрелочкой обозначено направление трубы). Рассмотрим Т-тетрамино, касающееся тремя клетками верхней горизонтально расположенной границы трубы и находящейся ближе всех к левой вертикальной границе (на рис. 10 обозначено серым цветом). Заметим, что существует два варианта того, как Т-тетрамино может «входить в поворот»: первый — когда выбранное нами Т-тетрамино касается левой вертикальной границы (см. рис. 10 А); второй — когда не касается (см. рис. 10 Б). Будем говорить «двуповорот начинается первым (вторым) способом».
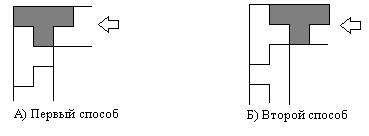
Рис. 10. Способы начала двуповорота
Теорема 1. Двуповорот хороший тогда и только тогда, когда его можно разбить на Т-тетрамино.
Доказательство.
Докажем индукцией по длине двуповорота — d.
База.d=1
Прямой двуповорот длины 1 можно разбить на Т-тетрамино двумя способами в зависимости от способа начала. (см. рис. 11)
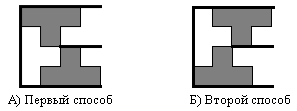
Рис. 11. Разбиение прямого двуповорота длины 1
Косой двуповорот длины 1 разбить на Т-тетрамино невозможно вне зависимости от способа начала. (см. рис. 12)
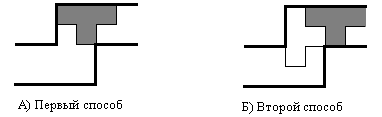
Рис. 12. Попытка разбиения косого двуповорота длины 1
d=2
Прямой двуповорот длины 2 разбить на Т-тетрамино невозможно вне зависимости от способа начала. (см. рис. 13)

Рис. 13. Попытка разбиения прямого двуповорота длины 2
Косой двуповорот длины 2 можно разбить на Т-тетрамино двумя способами в зависимости от способа начала. (см. рис. 14)
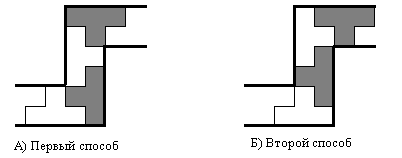
Рис. 14. Разбиение косого двуповорота длины 2
Индукционный переход.
По замечанию 1 очевидно, что последние доминошки двуповоротов длины d и d+2 принадлежат одной группе, значит если одна из них хорошая, то и вторая. Следовательно, двуповорот длины d можно замостить Т-тетрамино тогда и только тогда, когда двуповорот длиной d+2 можно замостить Т-тетрамино. Теорема доказана.
Утверждение. Если двуповорот начинался первым (вторым) способом и он разбит на Т-тетрамино, то следующий по направлению двуповорот также будет начинаться первым (вторым) способом.
Доказательство.
Докажем индукцией по длине изначального двуповорота d.
База. Рассмотрим прямой двуповорот (d=1) и косой двуповорот (d=2). Из рис. 11 и 14 видно, что следующий по направлению двуповорот начитается тем же способом, что и изначальный.
Индукционный переход. По замечанию 1 очевидно, что последние доминошки двуповоротов длины d и d+2 принадлежат одной группе, следовательно, следующие по направлению двуповороты будут начинаться одинаковым способом.
Замечание 2. Если двуповорот хороший, то его можно разбить на Т-тетрамино ровно двумя способами, определенными способом начала поворота.
Теорема 2. Труба хорошая тогда и только тогда, когда она разбивается на Т-тетрамино.
Доказательство.
Пусть труба хорошая. По утверждению верно, что, начав разбиение какого-то двуповорота и двигаясь по направлению трубы, мы сможем корректно разбивать трубу на Т-тетрамино и, дойдя до предыдущего по отношению к первому двуповороту, мы его начнём разбивать на Т-тетрамино тем же способом, каким начали заполнять первый двуповорот.
Пусть труба разбивается на Т-тетрамино.Если труба разбивается на Т-тетрамино, то все её двуповороты разбиваются на Т-тетрамино. По обратной Теореме 1 верно, что все двуповороты хорошие. Теорема доказана.
Утверждение. Для каждого разбиения прямоугольника 4mx 4n на K хороших труб существует ![]() разбиений этого прямоугольника на Т-тетрамино.
разбиений этого прямоугольника на Т-тетрамино.
Утверждение верно по замечанию 2.
В заключение сформулируем импликации, требующие отдельного рассмотрения.
Гипотеза 1. Если цикл хороший, то вершины сетки внутри него так же можно разбить на хорошие циклы.
Гипотеза 2. Для каждого хорошего цикла существует прямоугольник 4mx 4n, в разбиение сетки которого на простые циклы может входить данный цикл.
Гипотеза 3. Никаких других разбиений данного прямоугольника нет.
Литература:
- D. W. Walkup. Covering a rectangle with T-tetrominoes. Amer. Math. Monthly, 72:986–988, 1965.







