1. Introduction. Statement of the Problem.
In order to find an approximate representation of a function ![]() by elements of a certain finite collection, it is possible to use values of this function at some finite set of points
by elements of a certain finite collection, it is possible to use values of this function at some finite set of points ![]() ,
, ![]() . The corresponding problem is called the interpolation problem, and the points
. The corresponding problem is called the interpolation problem, and the points ![]() the interpolation nodes.
the interpolation nodes.
In the present paper we deal with optimal interpolation formulas. Now we give the statement of the problem of optimal interpolation formulas following by S. L. Sobolev. Now following we consider interpolation formula of the form
![]() (1.1)
(1.1)
where ![]() and
and ![]() (
(![]() ) are coefficients and nodes of the interpolation formula (1.1), respectively. We suppose that the functions
) are coefficients and nodes of the interpolation formula (1.1), respectively. We suppose that the functions ![]() belong to the Hilbert space
belong to the Hilbert space
![]()
equipped with the norm 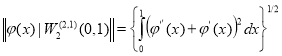 (1.2)
(1.2)
and 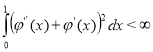 . The equality (1.3) is semi-norm and
. The equality (1.3) is semi-norm and ![]() if and only if
if and only if ![]() . The difference
. The difference ![]() is called the error of the interpolation formula (1.1). The value of this error at some point
is called the error of the interpolation formula (1.1). The value of this error at some point ![]() is the linear functional on functions
is the linear functional on functions ![]() , i.e.
, i.e.
![]()
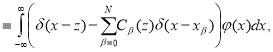 (1.3)
(1.3)
where ![]() is the Dirac delta-function and
is the Dirac delta-function and ![]() (1.4)
(1.4)
is the error functional of the interpolation formula (1.1) and belongs to the space
By the Cauchy-Schwarz inequality ![]()
the error (1.3) of formula (1.1) is estimated with the help of the norm
![]() of the error functional (1.4).
of the error functional (1.4).
Therefore from here we get the first problem.
Problem 1. Find the norm of the error functional ![]() of interpolation formula (1.1) in the space
of interpolation formula (1.1) in the space ![]() .
.
Obviously the norm of the error functional ![]() depends on the coefficients
depends on the coefficients ![]() and the nodes
and the nodes ![]() . The interpolation formula which the error functional in given number
. The interpolation formula which the error functional in given number ![]() of the nodes has the minimum norm with respect to
of the nodes has the minimum norm with respect to ![]() in the space
in the space ![]() is called the optimal interpolation formula. The main goal of the present paper is to construct the optimal interpolation formula in the space
is called the optimal interpolation formula. The main goal of the present paper is to construct the optimal interpolation formula in the space ![]() for fixed nodes
for fixed nodes ![]() , i.e. to find the coefficients
, i.e. to find the coefficients ![]() satisfying the following equality
satisfying the following equality ![]() (1.5).
(1.5).
Thus in order to construct the optimal interpolation formula in the space ![]() we need to solve the next problem.
we need to solve the next problem.
Problem 2. Find the coefficients ![]() which satisfy equality (1.5) when the nodes
which satisfy equality (1.5) when the nodes ![]() are fixed.
are fixed.
In this work we give the solution of Problem 1.
2. The extremal function and representation of the norm of the error functional
In this section we solve Problem 1, i.e. we find explicit form of the norm of
![]() The space
The space ![]() is the Hilbert space and the inner product in this space is given by the formula
is the Hilbert space and the inner product in this space is given by the formula 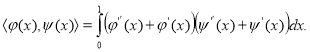 (2.1). According to the Riesz theorem any linear continuous functional
(2.1). According to the Riesz theorem any linear continuous functional ![]() in a Hilbert space is represented in the form of a inner product. So, in our case we have
in a Hilbert space is represented in the form of a inner product. So, in our case we have
![]() (2.2) for arbitrary function
(2.2) for arbitrary function ![]() from
from ![]() space. Here
space. Here ![]() is the function from
is the function from ![]() is defined uniquely by functional
is defined uniquely by functional ![]() and is the extremal function. Now we solve equation (2.2) and find
and is the extremal function. Now we solve equation (2.2) and find ![]() . Suppose
. Suppose ![]() belongs to the space
belongs to the space ![]() , where
, where ![]() is the space of functions, which are infinity differentiable and finite in the interval
is the space of functions, which are infinity differentiable and finite in the interval ![]() . Then from (2.1), integrating by parts, we obtain
. Then from (2.1), integrating by parts, we obtain
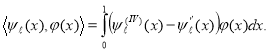 (2.3).
(2.3).
Keeping in mind (2.3) from (2.2) we get ![]() (2.4). So, when
(2.4). So, when ![]() the extremal function
the extremal function ![]() is a solution of equation (2.4). But, we have to find the solution of equation (2.2) when the functions
is a solution of equation (2.4). But, we have to find the solution of equation (2.2) when the functions ![]() belong to the space
belong to the space ![]() . Since the space
. Since the space ![]() is dense in the space
is dense in the space ![]() , then we can approximate arbitrarily exact functions of the space
, then we can approximate arbitrarily exact functions of the space ![]() by a sequence of functions of the space
by a sequence of functions of the space ![]() . Next for any
. Next for any ![]() we consider the inner product
we consider the inner product ![]() and, integrating by parts of (2.1), we have
and, integrating by parts of (2.1), we have
![]()
![]()
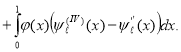
Hence from arbitrariness of ![]() and uniqueness of the function
and uniqueness of the function ![]() (up to the function
(up to the function ![]() and polynomials of degree
and polynomials of degree ![]() ), taking into account (2.4), it must be fulfilled the following equation
), taking into account (2.4), it must be fulfilled the following equation
![]() (2.5)
(2.5)
with boundary conditions
![]() (2.6);
(2.6);
![]() (2.7)
(2.7)
Thus, we conclude that the extremal function
Theorem 1. The solution of the boundary value problem (2.5)-(2.7) is the extremal function ![]() of the error functional
of the error functional ![]() of the interpolation formula (1.1) and has the following form
of the interpolation formula (1.1) and has the following form ![]() where
where 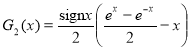 (2.8) is a solution of the equation
(2.8) is a solution of the equation
![]() (2.9)
(2.9) ![]() is any real number,
is any real number, ![]() is a polynomial of degree
is a polynomial of degree ![]() .
.
![]() (2.9),
(2.9),
![]() (2.10). Now we obtain representation for the norm of the error functional
(2.10). Now we obtain representation for the norm of the error functional ![]() . Since the space
. Since the space ![]() is a Hilbert space then by the Riesz theorem we have
is a Hilbert space then by the Riesz theorem we have ![]()
Hence, using (1.4) and Theorem 1, taking into account (2.9), (2.10), we get
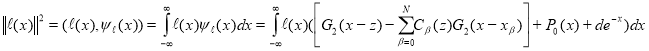
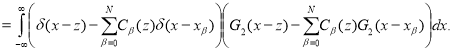 Hence and taking account that
Hence and taking account that ![]() is the even function, we have
is the even function, we have
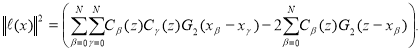 (2.11).
(2.11).
Thus Problem 1 is solved.
References:
- J. H. Ahlberg, E. N. Nilson, J. L. Walsh, The theory of splines and their applications, Mathematics in Science and Engineering, New York: Academic Press, 1967.
- S. L. Sobolev, Introduction to the Theory of Cubature Formulas, Nauka, Moscow, 1974, 808 p.







