Активные исследования алгебр Ли привели к возникновению нового алгебраического объекта — алгебр Лейбница. Алгебра Лейбница является обобщением алгебры Ли, для которого уникальное свойство алгебры Ли, а именно свойство оператора правого умножения быть дифференцированием, сохраняется. Понятие алгебры Лейбница было введено Лоде [4] как не антисимметрическое обобщение алгебр Ли. В течение последних 20 лет активно изучалась теория алгебр Лейбница, и многие результаты из теории алгебр Ли были продолжены до алгебр Лейбница. Из тождества Лейбница вытекает тот факт, что алгебры Лейбница заданной размерности образуют алгебраическое многообразие. Так как любое алгебраическое многообразие представляется в виде конечного объединения конечного числа неприводимых компонент, а они в свою очередь полностью описываются открытыми множествами, то важное значение при описании многообразий алгебр состоит в описании алгебр, у которых орбиты под действием линейной группы являются открытыми множествами. Алгебры с такими орбитами называются жесткими алгебрами.
Данная работа продолжает цикл изучения работ посвященной свойствам алгебр Лейбница начатой в работе [5]. В работе приводится пример такой алгебры изоморфной приведенной в работе [5].
Определение 1. Алгебра L над полем F называется алгеброй Лейбница, если для любых элементов x, y, zL выполняется тождество Лейбница:
[x, [y, z]] = [[x, y], z] — [[x, z], y],
Приведем определение групп когомологий для алгебр Лейбница. Для алгебры Лейбница L и ее представления М введем обозначения: Сn(L,M):=Hom(Ln,M), при n0 (при n<0, Сn(L,M) положим равным нулю). С*(L,M):= ![]() Сn(L,M). Элементы множества С*(L,M) будем называть коцепями L со значением в М, а элементы Сn(L,M) коцепями степени n.
Сn(L,M). Элементы множества С*(L,M) будем называть коцепями L со значением в М, а элементы Сn(L,M) коцепями степени n.
Пусть dn: Сn(L,M) Сn+1(L,M) гомоморфизм, определенный следующим образом:
(dnf)(x1,…,xn+1):= [x1,f(x2,…,xn+1)]+![]() (-1)i [f(x1,…,
(-1)i [f(x1,…, ![]() ,…,xn+1),xi]+
,…,xn+1),xi]+
+![]() (-1)j+1(f(x1,…,xi-1, [xi,xj],xi+1,…,
(-1)j+1(f(x1,…,xi-1, [xi,xj],xi+1,…,![]() ,…,xn+1),
,…,xn+1),
где fСn(L,M), хiL и символ ![]() означает отсутствие элемента х.
означает отсутствие элемента х.
Элементы ядра dn (обозначим Kerdn:=ZLn(L,M)) назовём n-коциклами, а элементы образа dn+1(обозначим Imdn+1:=BLn(L,M)) — n-кограницами. Очевидно, что BLn(L,M)ZLn(L,M). Фактор пространство HLn(L,M):=ZLn(L,M)/BLn(L,M) назовём пространством когомологий алгебры L степени n со значениями в М.
Для произвольной алгебры Лейбница L определим последовательности
L1=L, Lk+1= [Lk, L1], k 1.
L [1]=L, L [k+1] = [L [k], L [k]], k 1.
Определение 2. Алгебра Лейбница L называется нильпотентной (соответственно разрешимой), если существует sN такое, что Ls=0 (L [s]=0).
Определение 3. Алгебра Лейбница L размерности n называется филиформной, если dim Li= n–i, 2 i n.
Напомним, что в каждой размерности с точностью до изоморфизма существует одна естественным образом градуированная не разложимая и не Лиевая филиформная алгебра Лейбница. Такая алгебра обозначается через ![]() и в нём существуют базис {e1, e2, …, en}, такое, что умножение в этом базисе имеет вид [1]:
и в нём существуют базис {e1, e2, …, en}, такое, что умножение в этом базисе имеет вид [1]:
![]() : [e1,e1]=e3, [ei,e1]=ei+1,2≤i≤n–1.
: [e1,e1]=e3, [ei,e1]=ei+1,2≤i≤n–1.
В работе [3] получено описание разрешимых алгебр Лейбница с нильрадикалом ![]() .
.
Теорема 1 [3]. Пусть R1–разрешимая алгебра Лейбница с нильрадикалом ![]() , тогда dimR1=n+1 и существует базис {e1, e2, …, en, x} такой, что умножение в алгебре R1 имеет вид:
, тогда dimR1=n+1 и существует базис {e1, e2, …, en, x} такой, что умножение в алгебре R1 имеет вид:
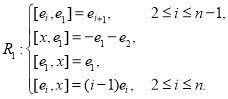
Напомним, что дифференцированием D алгебры L называется линейное преобразование, удовлетворяющее условию:
D(xy) = D(x)y + xD(y), x, y L.
В следующей предложении описаны пространства дифференцирований разрешимых алгебр Лейбница R1.
Предложение 1.Всякое дифференцирование алгебры ![]() , имеет следующий вид:
, имеет следующий вид:
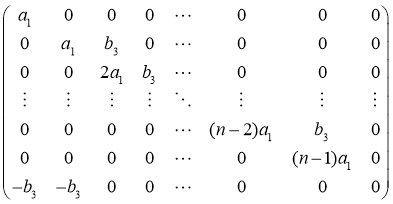 ,
,
Из определения множества BL2(R1, R1) и Предложения 1 нетрудно заключить, что DimBL2(R1, R1) = (n+1)2–2.
В следующей теореме мы приводим результат, в котором подсчитана размерность пространства ZL2(R1, R1).
Теорема 2.DimZL2(R1, R1)= (n+1)2–2.
Из определения второй группы когомологийHL2(R1,R1)=ZL2(R1,R1)/BL2(R1, R1) мы имеем, что HL2(R1, R1)=0.
Теорема 3.Aлгебра R1 жесткая в многообразия n+1 — мерных алгебр Лейбница.
Литература:
- Аюпов Ш. А. Омиров Б. А. О некоторых классах нильпотентных алгебр Лейбница. Сиб. Мат. Журнал, 2001. Т. 42. С. 18–29.
- Balavoine D. Déformations et rigidité géométrique des algebras de Leibniz. Comm. in Algebra. — 1996. — Vol. 24. — P. 1017–1034.
- Casas J.M, Ladra M., Omirov B. A. and Karimjanov I. A., Classication of solvable Leibniz algebras with naturally graded fililiform nilradical. Linear Algebra Appl., 438(7), p 2973–3000, 2013.
- Loday J.-L. Une version non commutative des algebres de Lie: les algebres de Leibniz. Enseign. Math. — 1993. — Vol. 39. — P. 269–293.
- Мамадалиев У. Х. Об одной жесткой разрешимой алгебре Лейбница. УзМЖ, 2013, № 3,-с70–78.







