Компенсация движения в цифровых динамических видеоизображениях является одной из важнейших задач компрессии видеоизображений по объёму кодируемой информации [1,2,3]. Сжатый по объёму сигнал при незначительном снижении качества декодируемого изображения, в общем случае, требует меньших энергетических затрат на его передачу по каналам связи, что оправдывает применение видеокодеков в составе современных цифровых телевизионных систем.
В современных видеокодеках компенсация движения проводится на фрагментарном уровне [1]. По результатам компенсации движения положения одних и тех же фрагментов изображения удаётся прогнозировать, сэкономив при этом машинное время.
Однако, вместе с тем, почти все современные видеокодеки используют анализ динамических свойств фрагментов по отдельности [1], в то время как очевидно, что можно обнаружить закономерности движения целых групп фрагментов.
С этой точки зрения перспективным представляется подход, использующий для анализа и прогнозирования движения математический аппарат векторных полей [4]. К примеру, (рис. 1.), при поступательном движении подвижного объекта навстречу видеокамере, фрагменты его плоскостных проекций удаётся охарактеризовать центральным векторным полем скоростей, абсолютные значения которых нарастают при удалении от центра поля к краям проекции.
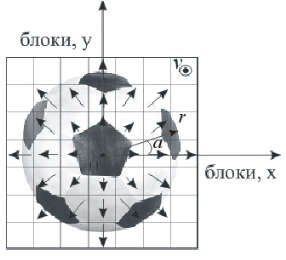
Рис. 1. Центральное векторное поле скоростей движения фрагментов изображения при поступательном движении пространственного объекта к кадровой плоскости
Абсолютные значения скоростей движения фрагментов проекции можно при этом задать пропорциональной зависимостью скорости от длины радиус-вектора, соответствующего определённому фрагменту (блоку):
![]()
где: v — вектор скорости в фиксированной точке изображения; r — радиус-вектор; k — коэффициент пропорциональности.
Тогда координаты очередного блока, при переходе от полярной системы координат к прямоугольной, можно вычислять по формуле:
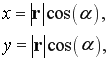
где: α — угол отклонения радиус-вектора в полярной системе координат, а для линейных скоростей движения блоков использовать формулы:
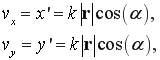
где: vx,vy — проекции вектора линейных скоростей в прямоугольной системе координат. При этом, угол отклонения радиус-вектора для каждого блока может быть однозначно определён по его индексам:
![]()
где: i,j — индексы блоков.
Отметим, что при движении пространственного объекта от видеокамеры, направления векторов скоростей движения блоков его проекции изменятся на противоположные, но поле при этом останется центральным (рис. 2.).
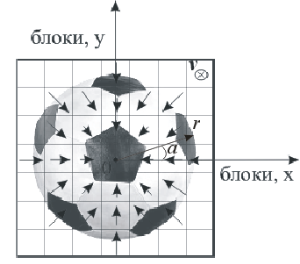
Рис. 2. Центральное векторное поле скоростей движения фрагментов изображения при поступательном движении пространственного объекта от кадровой плоскости
Формулы для расчёта модулей скоростей блоков, координат блоков и угла отклонения радиус-вектора, в этом случае, останутся прежними, а изменившееся направление векторов скоростей блоков можно учесть, поменяв знак коэффициента пропорциональности:
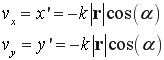
В любом случае, вне зависимости от того, каков характер поступательного движения пространственного объекта (к видеокамере или от неё), для использования центрального поля в декодере необходимо вычислить и передать на сторону декодирования всего три параметра: значение коэффициента пропорциональности, координаты центральной точки поля, а также признак того, что это поле центральное. При этом, характер поля будет уточнять положительное или отрицательное значения коэффициента пропорциональности.
Суть такого подхода состоит в том, чтобы по небольшому числу выбираемых предварительно опорных блоков восстановить параметры векторного поля скоростей блоков, а затем применить его для прогнозирования движения большого числа соседних блоков.
Данный подход иллюстрирует рисунок, представленный ниже (рис. 3.), где выбрано три опорных блока. Теоретически, для расчета значения коэффициента пропорциональности достаточно и двух опорных блоков. Однако, использование трёх блоков даёт более гибкий подход к анализу и идентификации параметров векторного поля.
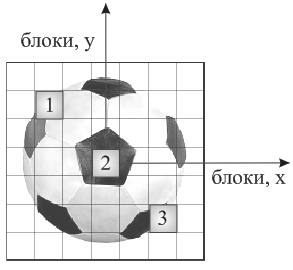
Рис. 3. Пример выбора опорных блоков для идентификации типа и параметров векторного поля.
В частности, открывает возможность использования математического аппарата векторных полей и объектов, связанных с этим разделом (градиент, дивергенция, ротор). Так, например, градиент (вектор частных производных) векторного поля скоростей блоков можно использовать проверяя по опорным блокам пару условий, согласно которым модули градиентов скоростей первого и третьего блоков должны быть равны между собой, а модуль градиента второго блока (центрального) должен стремиться к нулю:
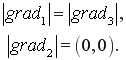
Одновременное выполнение указанных условий свидетельствует о том, что, возможно обнаружено центральное векторное поле. Таким образом, через градиенты некоторого набора опорных блоков изображения можно идентифицировать центральное векторное поле скоростей. Для того, чтобы дополнительно уточнить характер этого поля и определить направление скоростей блоков (от центра или к центру), достаточно проанализировать направление градиентов по углу α (градиенты могут быть противоположными, либо направленными друг к другу).
Используя дополнительно дивергенцию и ротор, удаётся обнаруживать не только центральное поле скоростей, но вихревое, безвихревое и другие виды векторных полей. Применение векторных полей, в свою очередь, позволяет охватить целую группу подвижных объектов, что впоследствии позволяет экономить машинное время на прогнозирование движения в кадре. Согласно результатам моделирования, по тройке опорных блоков удаётся выявлять векторные поля и прогнозировать движения групп блоков количеством 15–20 блоков.
При условии, что в кадре содержатся только крупные подвижные объекты неизменяемой геометрической формы, процесс компенсации движения в таких изображениях удаётся ускорить в несколько раз. Это, в свою очередь, позволяет на стороне декодирования в режиме on-line сделать процесс воспроизведения кадрового потока более плавным.
Литература:
- Ричардсон Я. Видеокодирование. Н.264 и МРЕG-4 — стандарты нового поколения. — М.: Техносфера, 2005. — 368с.
- Минаков Е. И. Калистратов, Д. С. Режимы формирования кадровых прогнозов в компенсаторах движения видеообъектов / Е. И. Минаков, Д. С. Калистратов // Известия Тул ГУ. Технические науки. Вып.11 Ч.2. Тула: Изд-во ТулГУ, 2012. С.188–193.
- Патент на изобретение № 2552139. Способ компенсации движения в цифровых динамических видеоизображениях / Минаков Е. И., Калистратов Д. С. Приоритет от 16.12.2013, опубл. 29.04.2015.
- Гаврилов В. Р., Иванова Е. Е., Морозова В. Д. Кратные и криволинейные интегралы. Элементы теории поля. — М.: Изд-во МГТУ им. Баумана,2003. — 496с.







