Перспективы развития швейной промышленности является одной из ведущих отраслей легкой промышленности. Ускорение научно-технического прогресса и рост эффективности производства неотделимы от резкого повышения качества продукции, что является самым точным и обобщающим показателем научно-технического прогресса. За качеством продукции на всех стадиях ее жизненного цикла несет ответственность те, кто причастен к ее разработке: ученые, конструкторы и дизайнеры. Решение проблем качества — первейшая обязанность каждого специалиста.
Проектирование в современном понимании — это совокупность (комплекс) работ по созданию нового образца изделия, включая исследование, технико-экономические расчеты и обоснования, создание эскизов, моделей, расчеты и построение чертежей изделий и деталей, изготовление и испытание опытных образцов.
На этапе математической обработки и хранения геометрической информации о лекалах швейных изделий выполняются следующие задачи:
‒ математическое описание контуров лекал в удобном и компактном виде, основанное на использовании методов аппроксимаций;
‒ геометрическое преобразование плоскостного отображения лекал из одной формы в другую, включающее операции сдвига изображений, сжатия или растяжения, поворота, отсечения части изображения, перекоса и т. д.
Математическим аппаратом для решения задач геометрического проектирования является вычислительная геометрия. Рассмотрим некоторые методы математического описания кривых.
В условиях САПР геометрическая информация о контурах поступает в ЭВМ в виде набора координат дискретных точек лекал. Для считывания координат используются различные устройства ввода графической информации. В результате в памяти машин накапливается большой объем исходной информации и возникает задача сокращения этого объема при сохранении точности задания контура.
Традиционно для математического описания контуров криволинейных участков лекал используются методы интерполяции и аппроксимации.
Интерполяция в простейшем смысле — это конструктивное восстановление функции определенного класса по известным ее значениям.
Аппроксимация — это замена одних математических объектов другими, близкими к исходным. В геометрическом проектировании аппроксимация сводится к замене дискретно заданного контура лекал кривыми, которые могут быть выражены через различные функциональные зависимости.
Так как швейные лекала имеют разнообразную сложную конфигурацию, описать единым уравнением весь контур практически невозможно, поэтому аналитическое описание дается на отдельные расчлененные участки. Кусочно-аналитическая модель, используемая для этих целей, представляет собой совокупность аналитических описаний простых участков и структуру соединений этих участков.
Наибольшее распространение при описании контуров получили методы кусочно-линейной, линейно-круговой и сплайновой аппроксимации. При кусочно-линейной аппроксимации осуществляется замена участков криволинейного контура отрезками прямых. При этом отклонение аппроксимирующих отрезков от исходных линий контура, называемое погрешностью аппроксимации, должно быть меньше заданной величины А. В результате аппроксимации контур или другие замкнутые линии швейного лекала заменяются многоугольниками, вершины которого называются узлами аппроксимации. Координаты узловых точек фиксируются в порядке их обхода.
Запись линейной интерполяции может быть представлена следующим образом. Каждый узел (участок кривой) выражаем через функцию
fi = S (хi), Ф (хi) =У i
где, S — длина аппроксимируемого участка; t= 1, 2, 3,..., п — число узлов аппроксимации; хi, yi — координаты i-ro узла аппроксимации.
Для xi < x < xi+1 имеем S1(x) = (l-t)fi + tfi+1,
где t= (x — xi)/hi; ht = x i+1 — xi.
Допустимая погрешность приближения А зависит от шага аппроксимации hi: чем меньше шаг hi тем точнее и ближе аппроксимирующий контур подходит к исходному.
Основной недостаток кусочно-линейной аппроксимации — большое количество узлов аппроксимации и негладкая форма контура. Линейное интерполирование нашло широкое применение при воспроизведении контура в обрабатывающих устройствах чертежей и в графопостроителях.
В настоящее время известно несколько алгоритмов линейно-круговой аппроксимации. В простейшем случае аппроксимация осуществляется путем проведения окружностей через последовательно расположенные тройки точек. При аппроксимации дугами окружностей необходимо определить радиус искомой окружности.
Предположим, что требуется произвести аппроксимацию дугой окружности контура, заданного рядом точек. Сначала определяется начальное значение радиуса приближающей дуги. Для этого через начальную и конечную точки контура (рис. 1.) проводятся нормали к контуру (А01 и В01). Отметим, что за нормаль можно принять линию, перпендикулярную прямой, которая соединяет две соседние точки контура.
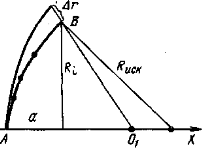
Рис. 1. Схематичное изображение аппроксимации контура дугой окружности с учетом допустимой ошибки: а — постоянный прогиб участка контура; Аг — абсолютное значение ошибки для конечной точки участка по отношению к выбранному значению
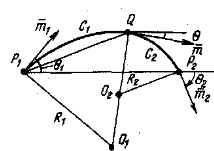
Рис. 2. Аппроксимация контура биарками при заданных углах: 01 = 50°; 0= –10°; 02= –70°
За начальное значение радиуса принимается расстояние от точки пересечения нормалей до начальной точки участка, т. е. Rн — А01. После этого строят дугу окружности радиуса А01 с центром в точке 01. Далее определяются постоянные для данного контура величины А г и а. А г — отклонение построенной дуги окружности от заданного контура определяется по формуле А г = В101 — В01.
Величина а определяется как проекция точки В1 на линию А01.
Для нахождения искомого радиуса Rиск используется формула
По этой формуле уточняется значение радиуса, которым и будет являться величина Rиск, а не Ri. По уточненному значению радиуса выбирается участок максимального отклонения точек заданного контура. Сравнивается выбранное значение с допустимым. Если Агмах превышает допустимое значение, то итерация продолжается; если нет — параметры аппроксимирующей дуги считаются найденными.
Для получения при аппроксимации более гладкой контурной линии может быть использован способ гладкой окружностной интерполяции, называемый способом биарок.
При аппроксимации через два соседних участка контура строится пара сопрягающихся дуг (С1 и С2) окружностей (рис. 2) так, чтобы дуга С1 проходила через точку Р1, касаясь вектора m1 а дуга С2 проходила через точку Р2, касаясь вектора m2.
Способом биарков можно практически аппроксимировать любой участок контура швейного лекала. В системах автоматизации процессов проектирования методы аппроксимации применяются не только для математического описания спроектированных контуров, но и прежде всего в целях конструирования кривых и поверхностей. При построении кривой в этих случаях утрачивает (или почти утрачивает) смысл такой математический критерий, как точность аппроксимации, и главную роль начинают играть такие критерии, как внешний вид и гладкость кривой, отсутствие осцилляций и т. п.
При аппроксимации швейных лекал математические методы не только позволяют сократить объем информации о контуре, но и улучшить эстетическое представление контура. Наибольшее распространение при математическом описании получили методы сплайн-аппроксимации. Термин «сплайн» возник от назначения чертежного инструмента — тонкой металлической линейки, которая может изгибаться так, чтобы проходить через заданные точки.
Предлагается два способа задания параметра t. В простейшем случае t задается как последовательность целых чисел: t j = j. При другом способе параметр t соответствует суммарной длине хорд, которая является аппроксимацией длины дуги между первой и j — й точками.
Литература:
- S.Tashpulatov, F.Alqarov, G.Alimova, Z.Xaqnazarova, B.Muxtorov, S.G’ofurova. Kiyimlarni kompyuterda loyihalash asoslari. — T., «Ilm ziyo». 2014.
- Д.Ткачев. Самоучитель AutoCAD. 2004. ЗАО. Издательский центр «Академия». 2010. — 176 с.
- Камилова Х. Х. и др. Методическое рекомендации по пользованию САПР одежды фирмы GERBER. ТИТЛП. — Ташкент, 2002.







