Интеграцияматематического и экономического знания в процессе обучения математики можно эффективно осуществить через специально составленную систему задач. Именно через задачи можно показать применение математических знаний для познания реального мира, познакомить учащихся с методами решения задач в науке и практической деятельности.
С такими задачами приходится иметь дело при оформлении в банке сберегательного вклада или кредита, покупке товаров в рассрочку, при выплате пени, налога, страховании ит.д.
Использование задач с экономическом содержанием на уроках и внеклассной работе по математике создает условия для:
а) разъяснения учащимся сущности экономических терминов, часто употребляемых в задачах;
б) формирования у учеников некоторых представлений об экономике страны;
в) воспитания у школьников бережного отношения к национальному богатству страны;
г) ознакомления учащихся с применением некоторых математических методов в экономике.
Задачи с экономическим содержанием мы подбираем к изучению из таких основных разделов математики, как числовые множества, алгебраические выражения, числовая последовательность и её предел, предел функции и непрерывность, производная и ее применение, интеграл т. д.
Пока в качестве поля деятельности здесь можно предложить следующий набор тем курса основ экономических знаний и соответствующих разделов курса математики.
|
Раздел математики |
Экономическое знание |
|
Числовые множества |
Затраты, доход, прибыль, проигрыш, себестоимость продукции, эффективность. Производительность труда и урожайность, средние величины, медиана, мода. Задачи экономического содержания на вычисления процентов |
|
Алгебраические выражения |
Валовой национальный продукт. Экономический рост. Вычисление уровня инфляции. Индексы цен. Закон денежного обращения. Уравнение Фишера. Реальная и номинальная заработная плата. Налоги. Вычисления налогов с заработной платы. Вычисление уравнения безработицы. Импорт и экспорт. Платежный баланс государства. Курсы валют |
|
Числовые последовательности и её пределы |
Банковские кредиты и проценты. Метод простых процентов. Амортизация займа. Вычисление кредитных процентов методом сложных процентов. Коэффициент наращения и сумма наращенного вклада. |
|
Функции и графики. Предел функции и непрерывность |
Постоянные и переменные издержки. Функция общих издержек. Валовой доход и функция прибыли. Производственные функции. Функции спроса и предложения. Определение рыночной (равновесной) цены. Совокупный спрос и совокупное предложение. Макроэкономическое равновесие. |
|
Производная и ее применение |
Эластичность спроса и предложения.Темпы изменения функций доходов, затрат и прибылей. Предельные (маржинальные) величины. Задачи на минимизации затрат и максимизацииприбыли. |
|
Интегральное исчисление функций одной переменной. |
Потребительские излишки и излишки производителя. Нахождение валового дохода, общих затрат и валовой прибыли с помощью функций маржинальных доходов, затрат и прибылей. Нахождение объёма выпуска предложения по известным функциям эластичностей спроса и предложения. Нахождение объёма выпуска продукции с помощью функции Кобба-Дугласа. Определение неравномерности распределения доходов среди населения (коэффициента Жини) |
Понятие числовой последовательности и её предел является одним из наиболее трудных понятий, вводимых в курс математики лицее. Поэтому особенно важно, кроме распространенных геометрических иллюстраций, рассмотреть с учащимися практические примеры экономического характера, помогающие лучше понять определение предела.
В некоторых экономических задачах, например, в задачах о денежных вкладах в сбербанке, возникает необходимость рассчитать так называемые «сложные проценты».
Мы говорим, что имеем дело со сложными процентами в том случае, когда величина в конце каждого этапа времени испытывает изменение на определенное число процентов, причем каждый раз начисление процентов происходит по отношению к тому значению рассматриваемой величины, которое образовалось в конце предыдущего этапа времени.
Выведем формулу для расчета сложных процентов. Допустим, что вкладчик открыл сберегательный вклад на сумму ![]() рублей сроком на
рублей сроком на ![]() лет, а ставка банковского процента составляет
лет, а ставка банковского процента составляет ![]() от суммы вклада на текущий период. Тогда по истечении первого года сумма начисленных банком процентов составит
от суммы вклада на текущий период. Тогда по истечении первого года сумма начисленных банком процентов составит ![]() рублей и на счете вкладчика будет
рублей и на счете вкладчика будет ![]() рублей (1)
рублей (1)
По прошествии второго года банк начислит ![]() уже на сумму
уже на сумму ![]() рублей и поэтому она увеличится на
рублей и поэтому она увеличится на ![]() , а в конце второго года на счете окажется
, а в конце второго года на счете окажется ![]() рублей.
рублей.
На основании равенства (1) получим, что
![]() (2)
(2)
Конце третьего года банк вновь начислит ![]() уже на сумму
уже на сумму ![]() рублей, а поэтому к концу года на счете вкладчика будет лежать уже
рублей, а поэтому к концу года на счете вкладчика будет лежать уже ![]() рублей, причем с учетом (2)
рублей, причем с учетом (2) ![]()
Аналогично можно показать, что по прошествии ![]() лет сумма денег на счете вкладчика достигает величины
лет сумма денег на счете вкладчика достигает величины
![]() (формула сложных процентов).
(формула сложных процентов).
Как видно из этой формулы, рост первоначальной суммы вклада по методу сложных процентов — это процесс, развивающийся по законам геометрической прогрессии, первый член которой равен ![]() , а знаменатель равен
, а знаменатель равен ![]() .
.
Пример 1. Фермер получил кредит в банке под определенный процент годовых. Через годфермер в счет погашения кредита вернул в банк от всей суммы, которую он долженбанку к этому времени, а еще через год в счет полного погашения кредита он внес в банк сумму на
Решение: Пусть ![]() — сумма кредита,
— сумма кредита, ![]() процент годовых по кредиту. В конце первого года фермер должен банку
процент годовых по кредиту. В конце первого года фермер должен банку ![]() рублей, а после частичной уплаты
рублей, а после частичной уплаты ![]() - рублей. К концу второго года фермер должен банку
- рублей. К концу второго года фермер должен банку ![]() рублей, что по условию задачи составило
рублей, что по условию задачи составило ![]() рублей. Таким образом, получаем уравнение тогда
рублей. Таким образом, получаем уравнение тогда ![]() , тогда
, тогда ![]() Ответ:
Ответ: ![]() годовых по кредиту в данном банке.
годовых по кредиту в данном банке.
К числу ![]() приводят решения многих прикладных задач статистики, физики, биологии, химии и др., анализ таких процессов, как рост народонаселения, распад радия, размножение бактерий и т. п.
приводят решения многих прикладных задач статистики, физики, биологии, химии и др., анализ таких процессов, как рост народонаселения, распад радия, размножение бактерий и т. п.
Рассмотрим задачу о непрерывном начислении процентов. Первоначальный вклад в банк составил ![]() денежных единиц. Банк выплачивает ежегодно
денежных единиц. Банк выплачивает ежегодно ![]() годовых. Необходимо найти размер вклада
годовых. Необходимо найти размер вклада ![]() через
через ![]() лет.
лет.
При использовании простых процентов размер вклада ежегодно будет увеличиваться на одну и ту же величину ![]() т. е.
т. е. ![]()
![]() …,
…,![]() На практике значительно чаще применяются сложные проценты. В этом случае размер вклада ежегодно будет увеличиваться в одно и то же число
На практике значительно чаще применяются сложные проценты. В этом случае размер вклада ежегодно будет увеличиваться в одно и то же число ![]() раз, т. е.
раз, т. е.
![]()
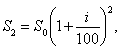 …,
…,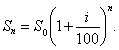
Если начислять проценты по вкладам не один раз в году, а ![]() раз, то при том же ежегодном приросте
раз, то при том же ежегодном приросте ![]() процент начисления за
процент начисления за ![]() ю часть года составит
ю часть года составит ![]() , а размер вклада за
, а размер вклада за ![]() лет при
лет при ![]() начислениях составит
начислениях составит 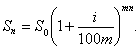
Будем полагать что проценты по вкладу начисляются каждое полугодие ![]() ежеквартально
ежеквартально ![]() ежемесячно
ежемесячно ![]() каждый день
каждый день ![]() каждый час
каждый час ![]() и т. д., непрерывно
и т. д., непрерывно ![]() Тогда размер вклада за
Тогда размер вклада за ![]() лет составит
лет составит

Формула выражает показательный (экспоненциальный) закон роста (при ![]() ) или убывания (при
) или убывания (при ![]() ). Она может быть использована при непрерывном начислении процентов.
). Она может быть использована при непрерывном начислении процентов.
Пример 2. Пусть темп инфляции составляет 20 % в год. Тогда реальная стоимость хранящихся дома денежных сбережений уменьшается. Насколько она уменьшается за месяц?
Решение. Применения формулы начисления непрерывных процентов дает
где ![]()
![]() хранящиеся дома денежные заначки приблизительно на 2 %.
хранящиеся дома денежные заначки приблизительно на 2 %.
Такие задачи выразительно демонстрируют практическую ценность математика и позволяют активизировать учебную деятельность.







