За последние годы количество устройств, которые работают с системами навигации резко возросло, и их становится все больше и больше с каждым днем. Область применения системы навигации действительно обширна — она находит свое приложение в совершенно различных сферах, таких как наука, технологии, экономика, туризм, исследования и наблюдения. А система повышения точности спутниковых сигналов (DGPS) при использовании спутниковой навигации может использоваться везде, где трехмерные геоданные играют особую роль.
Глобальные системы спутниковой навигации уже используются как нечто само собой разумеющееся в стандартной навигации (авиация и мореплавание), и чем дешевле и доступнее становится технология, тем больше появляется областей, в которых их применяют. К ним можно отнести: археологию, геофизику, геологию, картографию, географию, экологию, геодезию, физику, промышленность, тектонику, спутниковый мониторинг транспорта, активный отдых и геотеггинг. Также эта технология успешно используется в аэрокосмических и инженерных исследованиях, научных экспедициях, исследованиях леса и сельского хозяйства.
Наряду со спутниковой системой навигации существуют инерциальные системы навигации, которые имеют схожие области применения, но принципы их работы отличаются. Главной особенностью методов инерциальной навигации является автономность, то есть для того, чтобы определить координаты и параметры движения для инерциальной системы, в отличии от спутниковой, не требуется наличие внешних ориентиров или сигналов, поступающих извне, благодаря чему данные методы получают все более широкое применение.
На этапах тестирования и отладки комплексированной навигационной системы необходимо, чтобы все составляющие системы работали корректно и с большой точностью. Комплексированная навигационная система подвержена влиянию различных факторов, отрицательно влияющих на ее работу, что в конечном итоге отражается на результатах измерений. На этих этапах проводится тщательная проверка всех составных частей для обеспечения корректной работы всей системы.
Сегодня системы спутниковой навигации и инерциальные навигационные системы затрагивают многие аспекты нашей повседневной жизни, но в точных науках существуют задачи, где требуется высокая точность измерений. Так, для ряда задач в геодезии десятисантиметровой точности может быть недостаточно. В частности, при наличии десятисантиметровой ошибки площадь в 600 квадратных метров может измениться на 10 квадратных метров. В военном деле точность определения координат становится принципиальным вопросом, когда речь заходит о высокоманевренных объектах, к примеру, БПЛА или истребителях.
Для достижения требуемой точности измерений необходима организация решения множества мелких задач в режиме реального времени, в круг которых входят: прием и контроль данных информационных массивов первичных и вторичных навигационных параметров по; расчет из результатов измерений линейных ускорений и угловых скоростей по заданным осям объекта, номинального атмосферного давления, соответствующего высоте объекта, координат и векторов ускорений в различных системах координат (WGS-84, ПЗ-90.02, ПЗ-90.11 и другие), геодезических координат (широта, долгота, высота), ортометрической высоты, углов пространственной ориентации (курс, крен, тангаж); а также преобразование геодезических координат в пространственные прямоугольные и преобразование пространственных прямоугольных координат из одной системы в другую.
Для дальнейших расчетов будут использоваться некоторые данные, которые можно получить напрямую из навигационной аппаратуры (например, из сообщений протокола NMEA). К ним можно отнести:
‒ геодезические координаты,
‒ ортометрическую высоту,
‒ углы пространственной ориентации,
‒ вектор скорости относительно Земли в связанной с объектом геодезической системе координат.
Следующие параметры требуют расчета для обеспечения возможности проведения оценки.
Номинальное атмосферное давление, соответствующее высоте объекта-носителя.
Зависимость давления газа от высоты определяется барометрической формулой:
(1)
где h — разность высот — ортометрическая высота, м,
— молярная масса воздуха, 29 г/моль,
R — универсальная газовая постоянная, 8.31 Дж/(моль*К),
G — ускорение силы тяжести, 9.81 м/с2,
T — температура воздуха (К),
P0 — номинальное давление на исходной высоте (101 325 Па).
Таким образом, если в качестве
принять нормальное атмосферное давление (101 325 Па), то в качестве разности высот h будет выступать ортометрическая высота.
Координаты в прямоугольной связанной с Землёй системе координат получаем из геодезических координат и ортометрической высоты. Также для расчётов необходимо превышение геоида над референц-эллипсоидом, которое получаем из сообщения GGA протокола NMEA. Система координат, в которой получаем геодезические данные и высоту указана в сообщении DTM протокола NMEA.
Пересчёт геодезических координат в декартовы (координаты в прямоугольной связанной с Землёй системе координат) производится с помощью методов, установленных ГОСТ 51794–2008 «Глобальные навигационные спутниковые системы. Системы координат. Методы преобразований координат определяемых точек», который распространяется на системы координат, входящие в состав систем геодезических параметров «Параметры Земли», «Мировая геодезическая система» и координатной основы Российской Федерации и устанавливает методы преобразований координат и их приращений из одной системы в другую, а также порядок использования числовых значений элементов трансформирования систем координат при выполнении геодезических, навигационных, картографических работ с использованием аппаратуры потребителей глобальных навигационных спутниковых систем. Элементы трансформирования систем также приведены в ГОСТ 51794–2008 (WGS84 и ПЗ-90.2) и в справочном документе «ПАРАМЕТРЫ ЗЕМЛИ 1990 ГОДА» (ПЗ-90.11).
Преобразование геодезических координат в пространственные прямоугольные, в соответствии с указанными документами, производятся по следующим формулам:
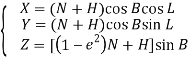(2)
где X, Y, Z — пространственные прямоугольные координаты точки,
B, L, H — геодезические координаты точки,
N — радиус кривизны первого вертикала,
e — эксцентриситет эллипсоида.
Радиус кривизны первого вертикала и квадрат эксцентриситета эллипсоида вычисляются по формулам:
(3)
(4)
где a — большая полуось эллипсоида,
— сжатие эллипсоида.
Углы пространственной ориентации (курс, крен, тангаж) получаем напрямую из информационных сообщений навигационной аппаратуры.
Введем нормальную систему координат OXgYgZg(по ГОСТ 20058–80), центр которой связан с центром масс объекта, ось OXg направлена на север по касательной к меридиану, ось OZg по касательной к параллели на восток, а ось OYg — вдоль вертикали места вверх. Также введём связанную систему координат OXYZ, центр которой связан с центром масс объекта, оси связаны с объектом. В таком случае углы курса (φ), крена (ψ) и тангажа (θ) — это углы поворота системы координат OXgYgZgдо системы координат OXYZ.
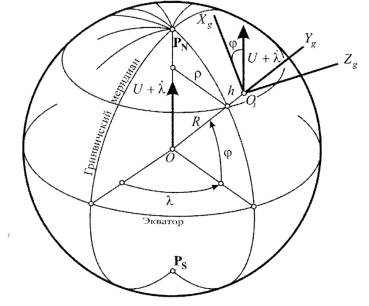
Рис. 1. Системы координат
Матрицу поворота (матрица направляющих косинусов) из связанной системы координат OXYZ (OBJ) в нормальную систему координат OXgYgZg (NORM) рассчитываем по формуле:
(5)
Таким образом, любой вектор 
в связанной системе координат (OBJ) может быть пересчитан в нормальную систему координат (NORM) по формуле:
(6)
Аналогичным образом рассчитываем матрицу поворота из нормальной системы координат, связанной с объектом, в геоцентрическую систему координат, связанную с Землёй (ECEF), учитывая, что широта и долгота объекта (B и L, геодезические координаты) — это и есть углы поворота ECEF до нормальной системы координат NORM. Тогда любой вектор
в нормальной системе координат, связанной с объектом (NORM) может быть пересчитан в геоцентрическую систему координат, связанную с Землёй (ECEF) по формуле:
(7)
Возможны и обратные преобразования, для этого достаточно определить обратную матрицу поворота по формуле:
(8)
Поскольку геодезические координаты могут быть посчитаны в системах координат WGS-84, ПЗ-90.02, ПЗ-90.11, то и матрицы поворота могут быть вычислены для любой из этих геоцентрических систем координат, связанных с Землёй (ECEF). Таким образом, имеется возможность пересчитать вектор в описанных системах координат в любую другую систему координат путём последовательных операций поворота.
Вектор скорости относительно Земли в связанной с объектом-носителем геодезической системе координат (ENU).
Компоненты вектора скорости 
, 
, 
относительно Земли в связанной с объектом-носителем геодезической системе координат (ENU) получаем напрямую из информационных сообщений навигационной аппаратуры. Система координат ENU — система координат, начало которой связано с центром масс объекта, а оси направлены на север, вертикально вверх и на восток. То есть эта система координат совпадает с нормальной системой координат, связанной с объектом (NORM), которая описана выше. Следовательно, компоненты вектора скорости относительно Земли в связанной с объектом-носителем геодезической системе координат (ENU) — это проекции вектора скорости относительно Земли на оси нормальной системы координат, связанной с объектом (NORM), а вектор выражается формулой:
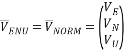(9)
Поскольку система координат ENU совпадает по ориентации с системой координат NORM, то и для поворота системы координат ENU можно применять матрицы поворота, рассчитанные для системы координат NORM.
Вектор скорости в прямоугольной связанной с Землёй системе координат.
Вектор скорости в прямоугольной связанной с Землёй системе координат получаем путём пересчёта вектора скорости относительно Земли в связанной с объектом-носителем геодезической системе координат (ENU) из системы координат, связанной с объектом, в систему координат, связанную с Землёй. Для этого используем матрицу поворота 
, рассчитанную выше. Итоговая формула:
(10)
Вектор ускорения относительно Земли в связанной с объектом-носителем геодезической системе координат (ENU).
Вектор ускорения относительно Земли в связанной с объектом‑носителем геодезической системе координат (ENU) получаем путём дифференцирования вектора скорости относительно Земли в той же системе координат. Формула выглядит следующим образом:
(11)
Вектор ускорения в прямоугольной связанной с Землёй системе координат.
Вектор ускорения в прямоугольной связанной с Землёй системе координат получаем путём пересчёта вектора ускорения относительно Земли в связанной с объектом-носителем геодезической системе координат (ENU) из системы координат, связанной с объектом, в систему координат, связанную с Землёй. Для этого используем матрицу поворота . Получается следующая формула:
(12)
Линейные ускорения по заданным осям объекта-носителя — это компоненты вектора ускорения относительно Земли в связанной системе координат объекта-носителя. Этот вектор определяем по формуле:
(13)
где 
— вектор ускорения относительно Земли в связанной с объектом-носителем геодезической системе координат (ENU),
— матрица поворота из геодезической системы координат, связанной с объектом в связанную систему координат объекта.
Угловые скорости по заданным осям объекта-носителя
Угловые скорости по заданным осям объекта-носителя получаем путём дифференцирования углов пространственной ориентации по следующим формулам:
(14)
Преобразование пространственных прямоугольных координат из системы А в систему Б.
Преобразование выполняется по формуле:
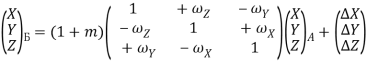(15)
В этой формуле приняты следующие обозначения элементов трансформирования:
, 
, 
— линейные элементы трансформирования систем координат при переходе из системы А в систему Б, м;
x, y,.z — угловые элементы трансформирования систем координат при переходе из системы А в систему Б, рад;
m — масштабный элемент трансформирования систем координат при переходе из системы А в систему Б.
С учетом представленных выше формул общая схема расчета выглядит следующим образом: при получении первичных и вторичных навигационных параметров, определяется системы координат, принятых данных, затем применяются формулы (2), (3), (4) для преобразования геодезических координат в пространственные прямоугольные. При необходимости производится трансформация пространственных прямоугольных координат из системы А в систему Б (15). Затем с использованием формул (5), (6), (7), (8) из геоцентрической системы координат, связанной с Землёй, производится перевод в нормальную систему координат, а из нормальной системы координат — в систему координат, связанную с объектом. Проводятся сопутствующие преобразования скорости и ускорения по формулам (10), (11), (12), (13). Таким образом, в системе координат, связанной с объектом, необходимо иметь данные, касающиеся линейных ускорений (13) и угловых скоростей (14).
В результате работы была исследована работа комплексированной навигационной аппаратуры и выработана общая последовательность преобразований и расчета параметров при ее оценке.
Литература:
- Яценков В. С. Основы спутниковой навигации. Системы GPS NAVSTAR и ГЛОНАСС. — М.: Горячая линия — Телеком, 2005. — 271 с.
- ГОСТ Р 51794–2008. Глобальные навигационные спутниковые системы. Системы координат. Методы преобразований координат определяемых точек // Помощь по ГОСТАМ. URL: http://www.gosthelp.ru/gost/gost48175.html (дата обращения: 20.04.2016)
- Богданов В. С., Кедров В. Д., Тазьба А. М. Особенности построения интегрированных инерциально-спутниковых навигационных систем // Информационно-управляющие системы. — 2005. — № 2. — С. 51–54.
