Ключевые слова:робастная статистика, непараметрическая статистика, регрессионный анализ, обработка данных
В современном мире все большую роль в промышленности приобретают автоматизированные системы. Для качественного управления технологическим процессом необходимо предварительное построение математической модели или идентификация и глубокое исследование процесса. Модели позволяют проводить качественный и количественный анализ объекта, а также прогнозировать его дальнейшее поведение.
Огромное влияние на адекватность будущей модели оказывают исходные данные, поэтому предварительная обработка данных приобретает особую значимость. Основная задача данного этапа — обработка аномальных измерений, выбросов (промахов), в исходной выборке. Причины появления аномальных наблюдений на практике очень разнообразны:
– сбой измерительной аппаратуры;
– искажение данных при их регистрации, передаче и хранении.
Присутствие нескольких выбросов может негативно отразиться на вычислении оценок параметров распределений и различных статистических характеристик.
Проблема обработки данных, содержащих резко выделяющиеся значения, давно известна. Даже одно такое незамеченное значение может значительно снизить точность анализа данных, а иногда и совсем его обесценить. Представление о том, какие значения считать резко выделяющимися, в большинстве случаев носят субъективный характер, так как оно основано на личном опыте исследователя. Исключение «плохих» данных по существу представляет «чистку» первичных данных перед обработкой и в ряде случаев является вполне допустимым. Однако, такая процедура тщательного просмотра данных возможна только для небольших выборок. Если объем данных велик, то их просмотр потребует столько времени и усилий, что вряд ли окажется реальным. Вместе с тем, практика обработки данных показывает, что появление резко выделяющихся значений в результатах наблюдений является скорее правилом, чем исключением. Таким образом, особое значение принимает возможность автоматизированной обработки резко выделяющихся наблюдений для больших объемов выборок.
Борьба с выбросами актуальна не только в идентификации, но и в любых вопросах, связанных со статистической обработкой данных. Проблемами определения выбросов и получения методов, устойчивых к выбросам, занимается раздел статистики называемый робастной статистикой. В статистике под робастностью понимают нечувствительность к малым отклонениям от предположений [1]. При обработке аномальных измерений были выработаны два подхода:
– исключение промахов из выборки;
– использование робастных методов обработки.
Термин «робастный» введен Джорджем Боксом в 1953 году для обозначения методов, устойчивых к малым отклонениям от предположений. Основы математической теории робастных оценок заложены Питером Хьюбером.
Выбросы (резко выделяющиеся наблюдения) — наблюдения, сильно отличающиеся от основной массы элементов выборки. Они обычно трактуются как грубые ошибки, возникающие в результате случайного просчета или неправильного чтения показаний измерительного прибора.
Робастная оценка — статистическая оценка, нечувствительная к малым изменениям исходной статистической модели. Также термин робастный переводится, как устойчивый, стабильный, помехоустойчивый.
Статистическая модель является приближением реальных процессов, если модель успешно описывает исследуемый объект, то говорят, что она адекватна, в противном случае неадекватна.
Непараметрическая статистика в самой исходной модели предполагает, что функциональный вид распределений, участвующих в задаче не известен. Приведем основные определения данного раздела статистики.
Непараметрическая задача — статистическая задача, в которой указываются только различия между классами распределений. По крайней мере, один из этих классов состоит из подчиняющихся некоторым довольно общим ограничениям, а в остальном неизвестных распределений. Такой класс распределений называется непараметрической гипотезой [3].
Непараметрическая статистика — ветвь математической статистики, занимающаяся рассмотрением непараметрических задач и связанных с ними теоретических проблем.
Непараметрические процедуры — алгоритмы решения непараметрических задач.
В непараметрическом случае оценка «параметров» возможна, если параметр есть известный функционал от неизвестного распределения. Оценка этого функционала, полученная без предположения о типе распределения, называется непараметрической.
Непараметрический факт — свойство выборки (или ее преобразований), которое не зависит от функционального вида распределения генеральной совокупности.
Методы непараметрической регрессии интенсивно развиваются в последние десятилетия. Повышенный интерес к сглаживанию обусловлен двумя причинами: статистики осознали, что параметрический подход не обладает необходимой гибкостью при оценивании, развитие вычислительной техники породило потребность в создании теории вычислительных методов непараметрического оценивания.
Регрессия описывает усредненную количественную связь между выходом и входом объекта. Методы непараметрической обработки информации работают при минимуме априорной информации, таким образом, иногда методы непараметрической регрессии применяют на начальной стадии анализа объекта для угадывания параметрического семейства зависимостей. Однако, универсальность методов компенсируется сложностью обработки исходной выборки, которую приходится хранить на протяжении всех вычислений. Вид функции регрессии может показать, для каких значений аргумента следует ожидать наибольшие значения наблюдений, также большой интерес представляют монотонность или унимодальность функции. Более того, иногда необходимо получить не функцию регрессии, а ее производные или другие функционалы.
При наличии наблюдений 
регрессионное соотношение может задаваться следующим образом:
(1)
где 
– неизвестная функция регрессии, а 
— ошибки наблюдения.
Цель регрессионного анализа состоит в осуществлении разумной аппроксимации неизвестной функции отклика 
. За счет уменьшения ошибок наблюдения становится возможным сконцентрировать внимание на важных деталях средней зависимости 
от 
при ее интерпретации. Эта процедура аппроксимации обычно называется «сглаживанием».
Главным вопросом, возникающим при построении непараметрической оценки, является степень сглаживания, которая определяется параметром сглаживания. Этот параметр управляет размером окрестности точки 
. Локальное усреднение по слишком большой окрестности не приводит к хорошим результатам. В этом случае происходит «чрезмерное сглаживание» кривой, приводящее к смещению оценки 
. Если определить параметр сглаживания так, что он будет соответствовать слишком малой окрестности, то в оценку регрессии будет вносить лишь небольшое количество точек, и мы получим грубое приближение.
Представим, что имеется процесс, общая схема которого изображена на рисунке 1.
Рис. 1. Общая схема процесса, принятая в теории идентификации: А — неизвестный оператор объекта; 
— выходная переменная процесса; 
— векторное управляющее воздействие; 
— векторное случайное воздействие; (
) — непрерывное время; 
— означают измерения 
, 
в дискретное время; 
— объем выборки; 
, 
— каналы связи, соответствующие различным переменным; 
, 
— случайные помехи измерений соответствующих переменных процесса
На вход объекта подается контролируемое воздействие 
, затем с помощью некоторого оператора преобразования получаем выходную переменную 
. Контроль переменных 
осуществляется через интервал времени 
через каналы связи 
и 
, то есть 
— выборка измерений переменных процесса 
. Случайные воздействия могут наблюдаться как в каналах связи, так и воздействовать на сам объект, поэтому аномальные измерения могут быть обнаружены, как при измерении входных, так и выходных данных. Таким образом, при исследовании объекта мы располагаем текущей информацией в виде выборки измерений 
, а также априорной информации о нем. В дальнейшем будем считать, что имеется объект с аддитивным шумом, помехи в каналах связи отсутствуют.
Пусть даны наблюдения 
случайных величин 
, 
распределенных с неизвестными плотностями вероятности 
(
— область значений 
), тогда непараметрическая оценка регрессии будет иметь следующий вид [2]:
(2)
где 
— точка, в которой восстанавливается функция регрессии 
или 
, при расчете не используется точка 
, 
— коэффициент размытости, главным образом определяющий степень сглаживания весовой функции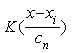 
, удовлетворяет некоторым условиям сходимости:
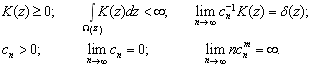(3)
На рисунке 2 приведены наиболее распространенные ядерные функции [2].
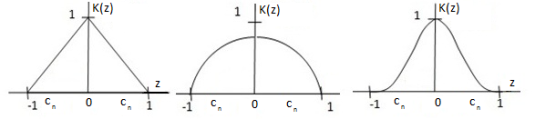
Рис. 2. Виды ядерных функций
(4)
(5)
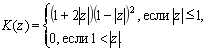(6)
В классическую непараметрическую регрессию 2 добавим весовую функцию 
, которая будет выполнять сглаживание по выходу 
.
Полученная робастная регрессия будет выглядеть следующим образом:
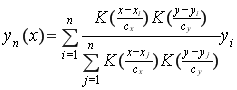(7)
Таким образом, оценка регрессии в точке будет строиться с учетом значений выходов соседних точек. Если точка, в которой восстанавливается значение, будет сильно отличаться от соседних, то такая точка является аномальной, и ядро 
будет равняться нулю.
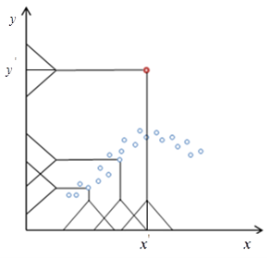
Рис. 3. Принцип работы алгоритма
На рисунке 3 красная точка является аномальной, значение 
сильно превосходит соседние точки в интервале 
, поэтому ни одна точка не попадает под весовую функцию 
, из чего следует, что оценка регрессии 
в точке 
будет равна нулю.
Параметр размытости 
определяется путем решения задачи минимизации квадратичного показателя соответствия выхода объекта и выхода модели, основанного на «методе скользящего экзамена», когда при построении модели не учитывается i-я пара измерений:
(8)
В многомерном случае, если каждой компоненте вектора 
соответствует компонента вектора 
, то во многих практических задачах 
можно принять скалярной величиной, если предварительно привести компоненты вектора 
, по выборке наблюдений, к одному и тому же интервалу, например, использовать операции центрирования и нормирования.
Настройку коэффициента размытости 
можно выполнять методом скользящего экзамена для обратной оценки регрессии.
В данной статье представлен алгоритм полного исключения выброса из исходной выборки. Если при изучении процесса имеется необходимое количество измерений, то при полном исключении точки из исходной выборки возможно более точное исследование.
Литература:
- Хьюбер П. Робастность в статистике. — М.: Мир, 1984. — 303 с.
- Рубан А. И. Методы анализа данных: учебное пособие. — 2-е изд. — Красноярск: ИПЦ КГТУ, 2004. — 319 с.
- Тарасенко Ф. П. Непараметрическая статистика. — Томск: изд. ТГУ, 1976. — 294 с.
