Пусть 
гильбертово пространство и 
линейный оператор с областью определения 
. Тогда множество 
называется числовым образом оператора 
[1–3]. Из определения видно, что множество 
является подмножеством комплексной плоскости и геометрические свойства дают некоторую информацию об операторе 
.
Изучение числового образа линейного оператора в гильбертовом пространстве является одним из основных методов в изучении местоположения спектра таких операторов. Это понятие впервые введено в работе [1] и доказано, что числовой образ матрицы содержит все её собственные значения.
В данной работе рассматривается 
симметричная матрица и исследован ее числовой образ в некоторых частных случаях.
Пусть 
— множество комплексных чисел. В пространстве 
рассмотрим матрицу вида:
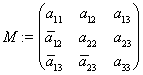
размера , где 
— произвольные вещественные числа, а 
— произвольные комплексные числа.
При этих предположениях матрица 
является линейным ограниченным и симметричным оператором в 
Лемма 1. Для числового образа матрицы 
имеет место равенство:
,
где 
собственные числа матрицы .
Доказательство. Пусть
— собственные числа матрицы . Обозначим через 
собственный вектор, соответствующий собственному числу 
матрицы 
а через 
собственный вектор, соответствующий собственному числу 
матрицы . Тогда имеет место соотношение:
, 
;
.
Очевидно, что квадратичная форма 
в единичной сфере 
достигает своего минимума при 
и достигает своего максимума при 
. Таким образом, .
Лемма 1 доказана.
Лемма 2. Если 
, то имеет место равенство:
.
Доказательство. Допустим , тогда:
.
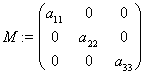Собственные числа матрицы являются нулями характеристического уравнения:
.
Отсюда следует, что для собственных чисел матрицы
верно 
. В силу леммы 1 имеем:
.
Лемма 2 доказана.
Лемма 3. Если 
, то имеет место равенство:
,где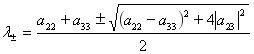 
.
Доказательство. Пусть . Тогда записывается как:
.
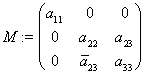Характеристическое уравнение матрицы имеет следующий вид:
(1)
Известно, что нули характеристического уравнения матрицы являются ее собственными числами. Таким образом, решение уравнения (1) приводится к решению уравнения:
и 
.
Отсюда следует, что:
.
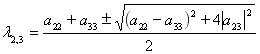Обозначим:
.
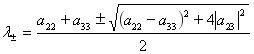Из леммы 1 следует, что:
.
Лемма 3 доказана.
Лемма 4. Пусть 
, тогда 
, где
.
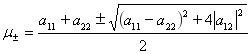Доказательство леммы 4 аналогично доказательству леммы 3.
Рассмотрим пример.
Вычислить числовой образ матрицы:
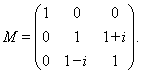
Решение. Видно, что 
. Так как 
, 
, следуя доказательству леммы 3 найдем остальные две собственные числа матрицы 
:
; 
.
В силу леммы 3 имеем 
.
Литература:
- Hausdorff F. Der Wertvorrat einer Bilinearform // Math. Z., 3:1 (1919), pp. 314–316.
- Heydari M. T. Numerical range and compact convex sets // Rend. Circ. Mat. Palermo, 60 (2011), pp. 139–143.
- Langer H., Markus A. S., Matsaev V. I., Tretter C. A new concept for block operator matrices: the quadratic numerical range // Linear Algebra Appl., 330:1–3 (2001), pp. 89–112.
