Расчет надежности железобетонных элементов конструкций



Расчет надежности железобетонных элементов конструкций

Неверова Елена Георгиевна, магистрант;

Гасратова Наталья Александровна, кандидат физико-математических наук, доцент

Санкт-Петербургский государственный университет

В работе приводится анализ надежности железобетонного изделия. В качестве объекта изучения рассматривается железобетонная балка. Исследованы особенности изменения физико-механических свойств бетона во времени. Построена функция надежности железобетонной балки при определенном типе нагружения (изгиб). Для решения поставленной задачи были использованы статистические данные, характеризующие прочность бетона на сжатие и арматуры — на растяжение.

Ключевые слова: надежность железобетонных изделий, функция надежности, расчет железобетонный балки, изгиб, прочность бетона на сжатие, прочность арматуры на растяжение

В современном строительстве одним из основных видов строительных материалов является железобетон. Обладая уникальными свойствами, железобетон позволяет решить множество проблем в строительстве: существенно снизить затраты, обеспечить прочность и долголетие, а также безопасную эксплуатацию конструкции при повышенной влажности, в экстремальных условиях и т. д.

Изучением параметров технических объектов, их закономерностей, анализом состояния и методами повышения работоспособности занимается теория надежности. Если речь идет о надежности строительных конструкций, то возникает необходимость в уточнениях в связи со спецификой изучаемых объектов. Важной особенностью механических систем, т. е. зданий и сооружений, является тот факт, что их надежность определяется надежностью отдельных несущих элементов конструкции, а также существенно зависит от ее структуры в терминах теории надежности (последовательная, параллельная или смешанная).

Определить надежность отдельно взятого элемента конструкции — непростая задача. Для ее решения необходимо предусмотреть множество определяющих факторов [16]. Однако эти факторы не всегда можно проанализировать детерминированными методами, например, точность монтажа конструкции или изменчивость условий изготовления конструкции. Поэтому, в данной работе будут рассмотрены наиболее существенные факторы, влияющие на надежность конструкции, такие как прочностные свойства материала [13,18]. Так, для железобетона необходимо учесть, что бетон — нелинейный материал [14, 19].

Основное требование к расчету надежности конструкции — это обеспечение ее прочности при эксплуатации. Прочность конструкции считается обеспеченной, если во всех поперечных сечениях ее элементов внутренние напряжения меньше предела прочности материала [7].

Произведем расчет надежности для элемента конструкции, одного из наиболее часто используемых в строительстве. Рассматривается балка, лежащая на двух шарнирных опорах, к которой приложена равномерно распределенная нагрузка. Вид нагружения балки — плоский изгиб (рис 1.).

Рис. 1. Расчетная схема

На рис. 1 — пролет балки, — прикладываемая нагрузка.

Расчет надежности элемента конструкции

Надежность строительного объекта — это свойство выполнять заданные функции в течение требуемого промежутка времени [11].

Надежность строительных объектов имеет определенную специфику. В ГОСТ 54257–2010 [1] в качестве основного показателя надежности строительных конструкций и оснований указана невозможность превышения предельных состояний, если на объект оказывает воздействие наиболее неблагоприятное сочетание нагрузок в течение некоторого срока службы.

С точки зрения теории надежности рассматриваемое в данной статье изделие является невосстанавливаемым объектом. Для невосстанавливаемых объектов основными критериями, определяющими надежность, являются [11]:

— вероятность безотказной работы объекта в течение времени ;

— вероятность отказа в течение времени ;

— наработка до отказа;

— плотность распределения времени безотказной работы;

— интенсивность отказа в момент времени .

Поскольку отказ элемента конструкции — это случайное событие, а момент времени до возникновения отказа — случайная величина, то надежность объекта можно описать некоторой функцией распределения продолжительности его безотказной
работы , определенной при . Таким образом, на основе данной функции распределения можно получить вероятность безотказной работы объекта в течение времени [11].

При анализе надежности элемента важно определить функцию распределения времени до отказа. Рассмотрим особенности построения функции надежности для решения поставленной задачи.

Вид нагружения балки — плоский изгиб, соответственно, при изгибе образуется сжатая и растянутая зоны. В растянутой зоне арматура работает на растяжение, в сжатой зоне бетон работает на сжатие (рис. 2).

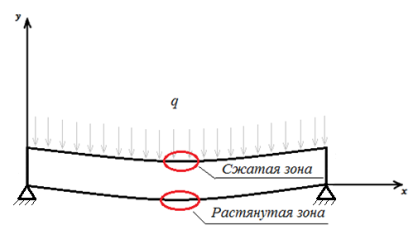
Рис. 2. Растянутая и сжатая зоны балки

Таким образом, необходимо рассмотреть прочностные свойства бетона на сжатие и арматуры — на растяжение [12, 17].

Расчет вероятности отказа ибезотказной работы элемента по прочности бетона на сжатие

Определим надежность бетонной части балки. Для этого рассмотрим изменение прочностных свойств бетона во времени, при этом необходимо учесть случайную природу значения величины прочности бетона.

Статистические данные позволяют проследить изменение прочности бетонного изделия во времени. В [10] приведена статистика данного параметра, а также коэффициент вариации прочности бетона, характеризующий изменчивость (колеблемость) значения случайной величины относительно среднего значения и, соответственно, однородность бетона (таблица 1).

Таблица 1

Изменение прочности бетона во времени

Возраст бетона, сутки	Количество образцов, шт.	Среднее значение прочности,	Коэффициент изменчивости,%
7 28 90 180 360 720	190 205 203 27 36 24	113 210 224 241 253 251	16,6 12,2 9,3 12,2 8,3 11,7

Считается, что при нормальных условиях твердения бетон принимает проектную прочность на 28 сутки.

Учитывая предположение о логарифмической зависимости прочности бетона от его возраста, предложенное Б. Г. Скрамтаевым [8], рассмотрим по имеющимся статистическим данным, приведенным в таблице 1, логарифмическую зависимость среднего значения прочности бетона от его возраста.

С помощью средств программы EXCEL построим график изменения прочности бетона во времени, построим линию тренда (аппроксимация и сглаживание) и выведем аппроксимирующую функцию (рис. 3).

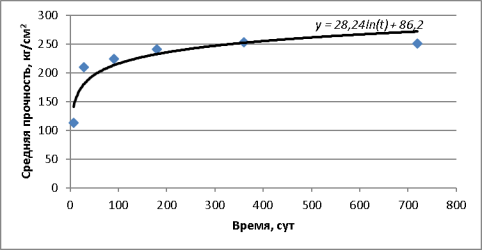
Рис. 3. Изменение прочности бетона во времени, аппроксимация логарифмической функцией

Получили функцию, имеющую вид

(1)

Таким образом, предложена новая зависимость прочности бетона от времени. Для практических расчетов такую зависимость целесообразно строить для каждого типа бетона.

Важно отметить, что вывод полученной выше функции изменения прочности бетона во времени (1) учитывает среднюю прочность определенного количества опытных образцов. Так как прочность опытного образца зависит от многих случайных факторов (качество заполнителя, влажность бетона, активность цемента и др.), то прочность каждого образца также является случайной величиной. Чтобы учесть случайную природу данного параметра, в нормах проектирования [4] предлагается использовать следующий способ получения расчетной прочности бетона: нормативная прочность умножается на коэффициенты надежности, определяемые с учетом факторов, влияющих на надежность конструкции, где нормативная прочность указана в нормативных документах для каждой марки бетона.

Во многих источниках [9, 10, 15] авторы, ссылаясь на статистику результатов экспериментов, указывают, что эмпирическое распределение прочности бетона может быть достаточно хорошо описано нормальным законом распределения. Хотя по данному вопросу у разных авторов есть противоречия [10].

Исходя из статистических данных (таблица 1) можно построить функцию распределения случайной величины значения кубиковой прочности бетона на сжатие в каждые сутки. Функция нормального распределения зависит от двух параметров: математического ожидания и среднего квадратического отклонения распределения. Данная функция может быть выражена через функцию Лапласа, значения которой берутся из соответствующей таблицы:

где

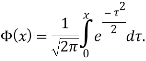
Значение параметра известны из Таблицы 1 (столбец 3). Значение параметра также можно вычислить из Таблицы 1 по значениям коэффициентов вариации прочности бетона (столбец 4) по формуле:

(2)

где — коэффициент вариации прочности бетона, и — математическое ожидание и среднее квадратическое отклонение, соответственно.

Исходя из специфики решаемой задачи — расчет балки, подверженной изгибу — в данном параграфе будем рассматривать только предел прочности бетона на сжатие, поскольку растягивающие напряжения принимаются арматурой.

По условию поставленной задачи необходимо, чтобы расчетные сжимающие напряжения не превышали некоторого допускаемого напряжения, то есть расчет проводится по допускаемым напряжениям. Для бетона условие прочности запишем в следующем виде [5, 7]:

(3)

где — наибольшие сжимающие напряжения в бетоне; — допускаемые напряжения сжатия бетона.

Допускаемое напряжение рассчитывается путем деления предела прочности на коэффициент запаса:

(4)

где предел прочности материала на сжатие, определяемые классом (маркой) бетона, — нормативный коэффициент запаса прочности, предписываемый нормами проектирования [3].

Согласно СНиП 2.03.01–84 [3] примем значение коэффициента запаса прочности равным

По данным таблицы 1 можно предположить, что испытанию на кубиковую прочность подвергались образцы бетона марки М200 (класса B15), так как на 28 сутки среднее значение предельной прочности на сжатие составило 210 кг/см². Предельная прочность бетона на сжатие для бетона марки М200 составляет [20].

Рекомендации по определению данного параметра представлены в ГОСТ 8462–85 [2]. Далее по формуле (4) рассчитывается допускаемое напряжение . Считаем, что — фиксированная величина.

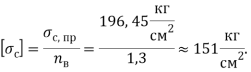(5)

Тогда можно рассчитать, с какой вероятностью прочность бетона не превысит допускаемого значения, то есть условие (3) запишем в виде

В случае нормального распределения вероятность того, что случайная величина примет значения в промежутке может быть вычислена по формуле [6]:

где — математическое ожидание случайной величины , — среднее квадратическое отклонение.

Пусть величина — прочность бетона на сжатие (случайная величина) в каждый момент времени , — средняя прочность бетона на сжатие, значения которой известны из таблицы 1, — среднее квадратическое отклонение из таблицы 1, определяемое по формуле (2). Тогда вероятность того, что прочность бетона будет в пределах вычисляется по формуле:

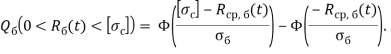(6)

Полученная формула позволяет рассчитать вероятность отказа бетонного изделия в момент времени . Тогда вероятность безотказной работы вычисляется по формуле

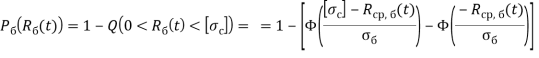(7)

По формуле (6) рассчитаем вероятность отказа бетона на сжатие на 28 сутки твердения. По формуле (1) значение равно

(8)

Подставим в (6) соответствующие значения из (5), из (8) и (известное из таблицы 1, причем, для расчета в другой момент времени, для которого нет табличного значения , используют приближенное значение [10]):

(9)

где и принимают табличные значения и по таблице значений функции Лапласа [21].

Из результатов данного расчета видно, что вторая часть в формуле (6) всегда принимает значение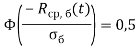 или, по крайней мере, стремится к этому значению при больших значениях . Иначе говоря, при расчете надежности бетонов высокой марки, средняя прочность на сжатие которых больше дисперсии не менее чем в пять раз, всегда имеем 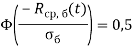, так как значение функции Лапласа при значении аргумента [6]. Тогда вероятность отказа будет определяться разницей между значениями и из первого слагаемого в формуле (9).

Найдем вероятность безотказной работы по формуле (7), подставив полученное значение из (9):

Далее рассмотрим прочностные свойства арматуры.

Расчет вероятности отказа ибезотказной работы элемента по прочности арматуры на растяжение

Согласно [10], распределение прочности арматуры чаще всего подчиняется нормальному закону. В [9] приведена гистограмма распределения прочности высокопрочной проволоки.

Данные гистограммы сведем в таблицу (таблица 2).

Таблица 2

Распределение прочности высокопрочной проволоки

Количество образцов, шт.	Значение прочности арматуры на растяжение ,
9 71 165 245 356 447 278 147 66 37 11	5123 5156 5180 5205 5238 5276 5303 5319 5367 5387 5424

Математическое ожидание для данного распределения равно , значение дисперсии , значение среднего квадратического отклонения .

Исходя из данных таблицы 2 можно предположить, что была рассмотрена арматура класса А500 [22].

Условие прочности арматуры на растяжение запишем аналогично (3) в виде

(10)

где — наибольшие растягивающие напряжения в арматуре; — допускаемые напряжения растяжения арматуры, значения которых определены для каждого класса арматура в [22]. Для арматуры класса А500 .

Функция надежности для нормального распределения случайной величины вычисляется по формуле [11]:

где 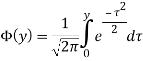— функция Лапласа, принимающая табличные значения [21], — математическое ожидание случайной величины , — среднее квадратическое отклонение случайной величины от математического ожидания.

Пусть — случайная величина прочности арматуры на растяжение, — математическое ожидание случайной величины , — среднее квадратическое отклонение случайной величины от математического ожидания , — допускаемые напряжения растяжения арматуры. Тогда вероятность безотказной работы арматуры при растяжении рассчитывается по формуле:

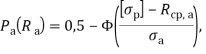(11)

Полученная формула обеспечивает выполнение условия (10).

Рассчитаем вероятность безотказной работы арматуры на растяжение по формуле (11) на примере арматуры, статистические данные для которой представлены в таблице 2.

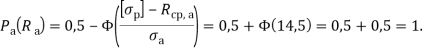
Исходя из полученного результата, можно сказать, что рассмотренный класс арматуры обеспечивает высокую степень надежности, что можно объяснить достаточным уровнем запаса прочности, установленного в нормах [22]. Из расчетов видно, что чем больше значение дисперсии случайной величины прочности арматуры на растяжение, тем меньше вероятность безотказной работы изделия, и чем меньше разница между математическим ожиданием случайной величины прочности арматуры на растяжение и допускаемым напряжением в арматуре, тем меньше вероятность безотказной работы.

Таким образом, зная вероятность безотказной работы бетона на сжатие (7) и вероятность безотказной работы арматуры на растяжение (11), получим вероятность безотказной работы железобетонной балки, работающей на изгиб (совместное появление двух событий), путем перемножения вероятностей:

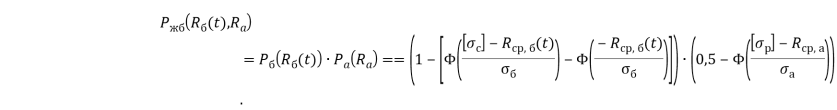(12)

Для примера, рассмотренного в данной работе, вероятность безотказной работы железобетонной балки будет определяться только работой бетона на сжатие, так как вероятность отказа арматуры равна 0, то есть

Расчет критериев надежности , , .

Далее рассмотрим такие критерии надежности, как плотность распределения времени безотказной работы , интенсивность отказа в момент времени и наработку до отказа [11].

Плотность распределения времени безотказной работы

Плотность распределения времени безотказной работы характеризует плотность
распределения случайной величины (момент времени до возникновения отказа). Эта величина наиболее полно характеризует
надежность конструкции в данный момент эксплуатации. Статистически может быть определено отношением числа отказавших образцов
конструкции (в единицу времени) к числу испытуемых образцов при условии, что
отказавшие образцы не восполняются исправными:

где — число отказавших образцов в течение промежутка времени
, — число испытуемых образцов.

С другой стороны, плотность распределения времени безотказной работы может быть найдена из следующей зависимости:

(13)

Вероятность безотказной работы элемента конструкции может быть вычислена по формуле (12). Перепишем эту формулу в виде:

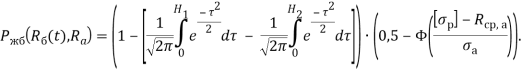
где , .

Тогда из (13) можно найти плотность распределения времени безотказной работы :

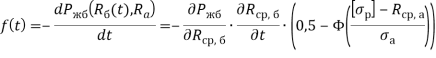
где 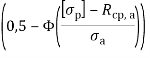не зависит от времени;

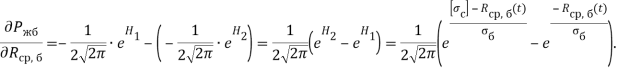
Тогда

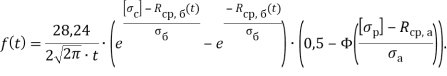
Определим значение данного показателя для железобетонной балки, характеризуемой статистическими данными из таблицы 1, в возрасте 28 суток.

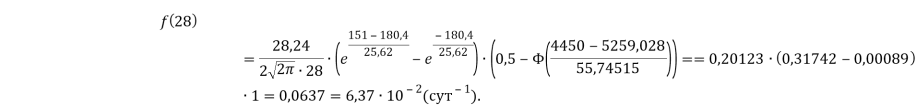
Таким образом, значение плотности распределение времени безотказной работы железобетонной балки в возрасте 28 суток равно . Полученная величина характеризует частоту отказов.

Интенсивность отказов

Интенсивность отказов определяется как отношение плотности распределения (13) времени безотказной работы к вероятности безотказной работы:

Рассчитаем значение на примере рассматриваемой в параграфе балки.

Статистически интенсивность отказов является отношением числа отказавших элементов к среднему числу исправно работающих образцов в течение времени :

где — среднее число исправных образцов в течение времени

Среднее время безотказной работы

Среднее время безотказной работы — это математическое ожидание времени безотказной работы элемента конструкции. Данный параметр можно вычислить, зная вероятность безотказной работы изделия, из следующего соотношения:

Рассчитаем значение для рассматриваемого в данном параграфе примера железобетонной балки:

Полученные результаты показывают, что статистические данные о материалах железобетонного изделия позволяют оценить надежность балки. В рассмотренном примере железобетонной балки, для бетона и арматуры которой была рассмотрена статистика (таблицы 1 и 2), низкий уровень надежности объясняется недостаточной обеспеченностью прочности бетона, тогда как арматура показала свою надежность благодаря большому запасу прочности на растяжение.

Выводы

Таким образом, в статье рассмотрены особенности построения функции надежности для железобетонной балки, лежащая на двух шарнирных опорах, к которой приложена равномерно распределенная нагрузка. Исследованы особенности изменения физико-механических свойств бетона во времени, оценены результаты теоретических исследований на конкретном примере, применен анализ статистических данных о кубиковой прочности бетона на сжатие и о прочности арматуры на растяжение. В результате были выведены формулы для расчета основных критериев надежности железобетонной балки.

Литература:

1. ГОСТ 54257–2010 «Надежность строительных конструкций и оснований». М., 2011.
2. ГОСТ 8462–85*. Материалы стеновые. Методы определения пределов прочности при сжатии и изгибе. М., 1985.
3. Пособие к СНиП 2.03.01–84* Бетонные и железобетонные конструкции. М., 1984.
4. СНиП 2.01.07–85*. Нагрузки и воздействия. М., 2003.
5. Аликин В. Н., Литвин И. Е., Сесюнин С. Г., Соколовский М. И., Ушин Н. В. Критерии прочности и надежность конструкций. М: Недра, 2005. 164 с.
6. Гмурман В. Е. Теория вероятностей и математическая статистика / Учебное пособие. М: Высшее образование, 2008. 479 с.
7. Дарков А. В., Шпиро Г. С. Сопротивление материалов. М: Высшая школа, 1975. 654 с.
8. Дворкин Л. И., Дворкин О. Л. Основы бетоноведения. СПб: Строй-бетон, 2006. 689 с.
9. Лычев А. С. Надежность строительных конструкций / Учебное пособие. М: Издательство Ассоциации строительных вузов, 2008. 184 с.
10. Лычев А. С., В. П. Корякин. Надежность железобетонных конструкций. Куйбышев: КуИСИ, 1974. 126 с.
11. Половко А. М., Гуров С. В. Основы теории надежности. СПб.: БХВ-Петербург, 2006. 704 с.
12. Гасратова Н. А. Решение некоторых классических пространственных задач теории упругости в напряжениях // Молодой ученый. 2014. № 3 (62). С. 1–6.
13. Гасратова Н. А., Старева И. А. Расчет надежности железобетонных конструкций // Устойчивость и процессы управления. Материалы III международной конференции. 2015. С. 349–350.
14. Кабриц С. А., Мальков В. М., Мансурова С. Е. Нелинейные уравнения плоского слоя для трех моделей эластомерного материала // Известия Российской академии наук. Механика твердого тела. 2001. № 1. С. 38.
15. Каприелов С. А., Травуш В. И., Карпенко Н. И., Шейнфельд А. В., Кардумян Г. С., Киселева Ю. А., Пригоженко О. В. Модифицированные высокопрочные бетоны классов В80 и В90 в монолитных конструкциях, часть 2 // Строительные материалы, № 3, 2008. С. 9–13.
16. Неверова Е. Г. К вопросу о влиянии наличия трещин на надежность строительных конструкций // Устойчивость и процессы управления. Материалы III международной конференции. 2015. С. 386–387.
17. Gasratova N. A. Study of building an analytical solution of the axisymmetric problem of linear elasticity in stresses as exemplified by finding the stress-strainstate of an ellipsoid concavity under the inner pressure // ARPN Journal of Engineering and Applied Sciences. 2014. T. 9. № 11. C. 2259–2267.
18. Gasratova N. A., Stareva I. A. Reliability assessment of reinforced concrete structures // 2015 International Conference “Stability and Control Processes” in Memory of V. I. Zubov (SCP). 2015. P. 378–381
19. Kabrits S. A., Kolpak E. P. Numerical study of convergence of nonlinear models of the theory of shells with thickness decrease // AIP Conference Proceedings 2015. C. 300005.
20. Таблица соотношения марок и классов бетона [Электронный ресурс] http://aquagroup.ru/articles/klass-i-marka-betona.html (Дата обращения: 10.04.16).
21. Таблица значений функции Лапласа [Электронный ресурс]. http://kvm.gubkin.ru/pub/fan/laplasetable2.pdf (Дата обращения: 10.04.16).
22. Нормативные и расчетные характеристики арматуры [Электронный ресурс]. http://asf.ugntu.ru/pg-06–01/ [zhbk]_harakteristiki_armaturi.pdf (Дата обращения: 10.04.16).