Исследование напряженно-деформированного состояния железобетонной балки при наличии трещины



Исследование напряженно-деформированного состояния железобетонной балки при наличии трещины

Гасратова Наталья Александровна, кандидат физико-математических наук, доцент;

Старева Ирина Александровна, магистрант

Санкт-Петербургский государственный университет

В работе исследовано напряженно-деформированное состояние железобетонной балки при наличии поперечной трещины. Приведена оценка численных результатов значений напряжений при удалении от вершины трещины. Моделирование осуществлялось с использованием пакета ANSYS.

Ключевые слова: напряженно-деформированное состояние, железобетонные изделия, трещины, моделирование, конечно-элементные методы.

Железобетон — это композиционный строительный материал, который, несмотря на то, что был открыт сравнительно недавно (первые патенты на использование железобетонных изделий были получены Жозефом Монье в 1867 году), находит широчайшее применение в современном строительстве. Этот факт вызван, в первую очередь, такими положительными качествами железобетона как долговечность, высокая пожаростойкость, низкая стоимость, а также высокая сопротивляемость статическим и динамическим нагрузкам.

Тем не менее, под влиянием внешних факторов, силовых воздействий, из-за недостаточно точных вычислений при проектировании либо просто с течением времени железобетонные конструкции, как и изделия из любых других материалов, подвержены различным разрушениям [1–5]. Одним из видов такого разрушения является трещинообразование в бетоне. Наличие трещин приводит к ослаблению всей конструкции, а в некоторых случаях может послужить и причиной для полного разрушения строения.

В связи с этим необходимо уделить особое внимание составлению и анализу моделей имеющихся конструкций либо сооружений, находящихся в стадии разработки, для выявления наиболее слабых мест постройки, а также анализа состояния изделия при наличии разнообразных дефектов [6, 7]. В данной работе уделяется внимание зависимости напряженно-деформированного состояния железобетонной балки при наличии поперечной трещины.

1. Диаграмма деформирования бетона

В современной литературе значительное место занимают труды, посвященные исследованию плосконапряженного состояния пластины с имеющейся трещиной [8]. Тем не менее, большинство из них, также как и анализ напряженно-деформированного состояния других разнообразных изделий, проведены с использованием линейной теории упругости [9–13], что не всегда бывает применимо на практике. В случае если рассматриваемый материал обладает нелинейными физическими или геометрическими свойствами, применение линейной теории упругости может дать абсолютно недостоверные результаты, что может привести к непоправимым последствиям. Поэтому исследования в области нелинейной теории упругости представляют определенный интерес [14, 15].

Поскольку бетон — материал, обладающий нелинейными физико-механическими свойствами, классический закон Гука для определения связи между деформациями (ε) и напряжениями (σ) имеет место только в случае малых деформаций. В связи с этим при моделировании изделий из бетона не рекомендуется основываться на линейном законе Гука, поскольку это может привести к некорректным результатам. Для достоверного анализа необходимо дополнительно задать диаграмму деформирования бетона, которая позволит определить связь между σ и ε. Никулин А. И. [16] для описания диаграмм сжатия бетона при центральном нагружении предлагает использовать дробно-рациональную функцию вида:

σ_b = E_b01ε_b(1+D_b01ε_b)/(1+C_b01ε_b), (1)

где E_b01, D_b01, C_b01 — начальный модуль упругости и параметры нелинейности деформирования бетона, получаемые экспериментально-теоретическим путем; σ_b, ε_{b —} текущие значения напряжений и деформаций сжатия. Для бетона класса B30 данные параметры принимаются равными E_b01 = 38519.0 МПа; D_b01 = –146.34; C_b01 = 738.49.

Диаграмма, основанная на (1), имеет вид, представленный на рисунке 1.

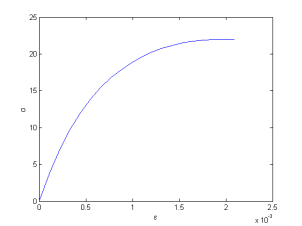
Рис. 1. Диаграмма деформирования бетона

3. Построение модели

Для исследования влияния наличия трещины на напряженно-деформированное состояние железобетонной конструкции с помощью ANSYS моделируется блок бетона с использованием типа элемента SOLID65 (рисунок 1: а) [17–19]. Блок обладает следующими геометрическими размерами: длина a = 3 м, ширина, b = 0.4 м, высота h = 0.4 м. Начальный модуль упругости бетона принимается равным E_b = 32.5*10⁹ Па, что соответствует тяжелому бетону естественного твердения класса B30. Коэффициент Пуассона ν_b = 0.18. Тяжелый бетон ρ_b = 2300 кг/м³. Для сравнения также приводится анализ напряженно-деформированного состояния блока, упрочненного четырьмя стержнями арматуры (рисунок 1: б). Радиус арматуры принимается равным r_a = 0.01 м. Коэффициент Пуассона для стали ν_a = 0.3, модуль Юнга E_a = 210*10⁹ Па.

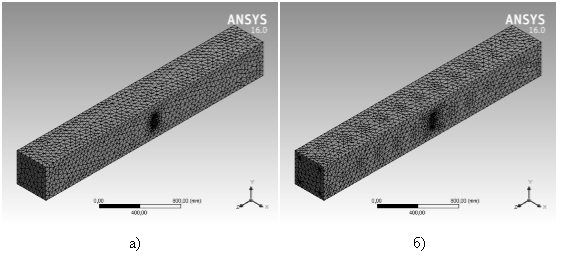
Рис. 2. Модель: а) блок бетона; б) блок бетона, армированный четырьмя стержнями арматуры

4. Исследование напряженно-деформированного состояния железобетонной балки при наличии поперечной трещины.

При наличии поперечной трещины, имеющей полудлину l = 5 см, картина распределения напряжений σ_zz и перемещений по оси OZ, в случае закрепления правой границы и приложения растягивающего напряжения σ₀ = 5 МПа к блоку бетона, представлена на рисунке 3.

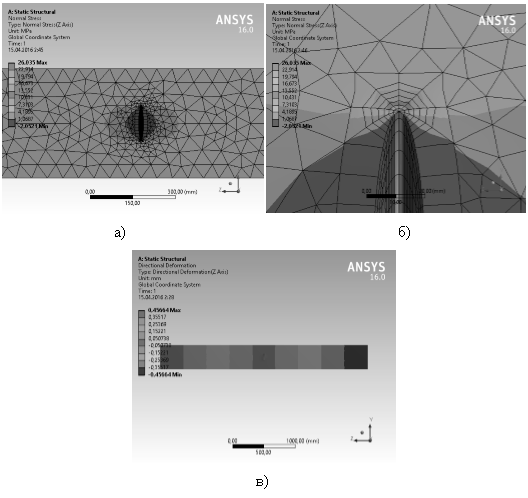
Рис. 3. Напряженно-деформированное состояние при наличии поперечной трещины (нелинейный случай): а) напряжения σ_zz [МПа]; б) напряжения σ_zz [МПа] в окрестности вершины трещины; в) перемещения

В случае рассмотрения бетона как линейного материала (что допустимо, если моделировать бетон на стадии, близкой к заливке) значения напряжений и перемещений будут отличаться от предыдущего случая (рисунок 4).

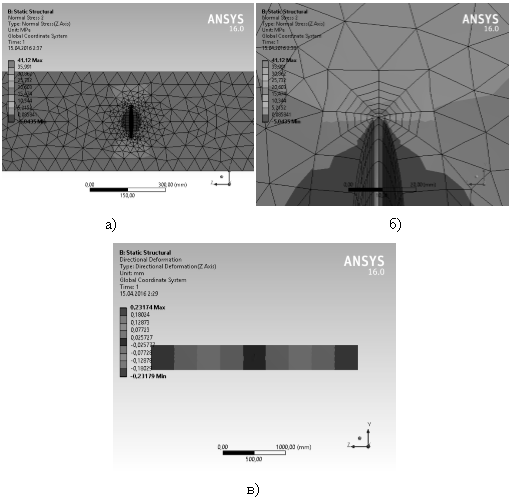
Рис. 4. Напряженно-деформированное состояние при наличии поперечной трещины (линейный случай): а) напряжения σ_zz [МПа]; б) напряжения σ_zz [МПа] в окрестности вершины трещины; в) перемещения

Согласно [8] распределение напряжений при удалении от вершины трещины определяется по формуле

(2)

При θ = 0 данное выражение примет вид

(3)

Решение, полученное по формуле (3), может быть использовано как аналитическая оценка для численных результатов значений напряжений при удалении от вершины трещины.

Графики изменения напряжений при удалении от вершины по оси трещины имеют вид, представленный на рисунке 5.

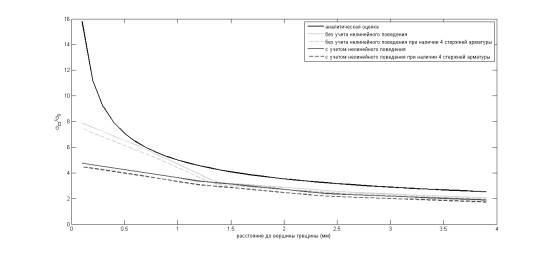
Рис. 5. Графики изменения напряжений при удалении от вершины трещины

На основе полученных графиков можно сделать вывод о том, что в случае рассмотрения модели по линейной теории упругости, распределение напряжений при удалении от вершины трещины имеет более схожую картину с аналитической оценкой. Учет же диаграммы деформирования бетона дает значительное влияние на значение напряжений в непосредственной близости к вершине трещины, при удалении же от нее, графики стремятся к близким значениям.

Кроме этого, из формулы (2), которая основана на линейной теории упругости, следует, что значения напряжений в вершине трещины должны достигать ∞ (при r = 0), что не имеет физического смысла. Это также подтверждают Г. Н. Албаут, Н. В. Харинова и М. Х. Ахметзянов [20]. Поэтому на сегодняшний день требуют доработки аналитические методы исследования рассматриваемых задач.

Наличие продольной арматуры (4 стержней диаметром d = 2 см) позволяет увеличивать прочность конструкции в случае наличия трещин за счет уменьшения максимальных значений напряжений σ_zz. Относительная разность для случая учета нелинейных свойств бетона составляет порядка 6.5 %, в случае моделирования по линейной теории упругости, данное значение соответственно 5 %.

5. Заключение

В работе проведен анализ картины распределения напряжений в окрестности вершины трещины, на основании чего сделан вывод о значительном влиянии нелинейных физико-механических свойств материала не только на значения максимальных напряжений, но и на картину в целом.

Литература:

1. Sedova O. S., Pronina Y. G. Initial boundary value problems for mechanochemical corrosion of a thick spherical member in terms of principal stress // AIP Conference Proceedings. 2015. P. 260002.
2. Pronina Y. G., Sedova O. S., Kabrits S. A. On the applicability of thin spherical shell model for the problems of mechanochemical corrosion // AIP Conference Proceedings. 2015. P. 300008.
3. Pronina Y. G. Analytical solution for decelerated mechanochemical corrosion of pressurized elastic-perfectly plastic thick-walled spheres // Corrosion Science. 2015. T. 90. C. 161–167.
4. Sedova O., Khaknazarova L., Pronina Yu. Stress concentration near corrosion pit on the outer surface of a thick spherical member // Tenth International Vacuum Electron Sources Conference (IVESC) & Second International Conference on Emission Electronics (ICEE) 2014. C. 245–246.
5. Пронина Ю. Г. Равномерная механохимическая коррозия полой сферы из идеального упругопластического материала под действием постоянного давления // Вестн. С.–Петерб. ун–та. Сер. 1: Математика. Механика. Астрономия. 2009. Вып. 1. С. 113–122.
6. Гасратова Н. А., Старева И. А. Расчет надежности железобетонных конструкций // Устойчивость и процессы управления. Материалы III международной конференции. 2015. С. 349–350
7. Gasratova N. A., Stareva I. A. Reliability assessment of reinforced concrete structures // 2015 International Conference “Stability and Control Processes” in Memory of V. I. Zubov (SCP). 2015. P. 378–381
8. Николаева Е. А. Основы механики разрушения. Учебное пособие. Издательство Пермского государственного технического университета, 2010. 103 с.
9. Гасратова Н. А. Решение некоторых классических пространственных задач теории упругости в напряжениях // Молодой ученый. 2014. № 3 (62). С. 1–6.
10. Gasratova N. A. Study of building an analytical solution of the axisymmetric problem of linear elasticity in stresses as exemplified by finding the stress-strainstate of an ellipsoid cocavityunder the inner pressure // ARPN Journal of Engineering and Applied Sciences. 2014. T. 9. № 11. C. 2259–2267.
11. Гасратова Н. А. Напряженно-деформированное состояние упругого пространства со сферическим включением // Вестник Санкт-Петербургского университета. Серия 10. Прикладная математика. Информатика. Процессы управления. 2009. № 1. С. 14–18.
12. Гасратова Н. А., Шамина В. А. Решение в напряжениях линейной осесимметричной задачи для сферы и упругого пространства со сферической полостью // Вестник Санкт-Петербургского университета. Серия 1. Математика. Механика. Астрономия. 2008. № 2. С. 122–128.
13. Гасратова Н. А., Шамина В. А. Об одном подходе к решению осесимметричных задач линейной теории упругости // Вестник Санкт-Петербургского университета. Серия 1. Математика. Механика. Астрономия. 2007. № 2. С. 101–106.
14. Kabrits S. A., Kolpak E. P. Numerical study of convergence of nonlinear models of the theory of shells with thickness decrease // AIP Conference Proceedings 2015. C. 300005.
15. Кабриц С. А., Мальков В. М., Мансурова С. Е. Нелинейные уравнения плоского слоя для трех моделей эластомерного материала // Известия Российской академии наук. Механика твердого тела. 2001. № 1. С. 38.
16. Никулин А. И. Энергетический подход к трансформированию эталонных диаграмм сжатия бетона // Бетон и железобетон. — 2013. — № 5, стр. 12–13
17. Hemamalini, S., Gopinathan, S. Behaviour of concrete structure under impact and blast load // International Journal of Applied Engineering Research 10 (5), 2015, pp. 13261–13282
18. Vasudevan, G., Kothandaraman, S. RC beams retrofitted using external bars with additional anchorages-a finite element study // Computers and Concrete 16 (3), 2015, pp. 415–428
19. Musmar, M.A., Rjoub, M.I., Abdel Hadi, M. A. Nonlinear finite element analysis of shallow reinforced concrete beams using solid65 element // ARPN Journal of Engineering and Applied Sciences. 9 (2), 2014, pp. 85–89
20. Албаут Г. Н., Харинова Н. В., Ахметзянов М. Х. Исследование геометрически и физически нелинейных проблем механики твердого тела методом нелинейной фотоупругости // Ученые записки Казанского университета. Серия Физико-математические науки № 4, 2010. с. 77–85