Роль графического метода в принятии управленческих решений. Поиск возможных улучшений путем анализа на чувствительность



Успех любого предприятия сильно зависит от принимаемых руководителем управленческих решений. Зачастую, руководители принимают их, основываясь на своем личном опыте и интуиции, однако данный подход никак не гарантирует того, что принятое решение будет наиболее выгодным в сложившейся ситуации. В то же время, существует множество инструментов, способных помочь в данном вопросе. Одним из таких является математический аппарат теории принятия решений, который можно использовать практически в любой ситуации [2].

Алгоритм принятия решения выглядит следующим образом:

1. Возникновение проблемной ситуации;
2. Выявление проблемы;
3. Постановка задачи;
4. Поиск решения;
5. Использование решения.

От третьего этапа напрямую зависит выбор метода, с помощью которого будет найдено решение. Одним из наиболее простых и с легкостью используемых является графический метод решения задач линейного программирования [1]. В таких задачах чаще всего есть два неизвестных (решение с тремя провести данным методом без использования специального программного обеспечения крайне затруднительно), для которых любую задачу можно представить в графическом виде и решить ее. Рассмотрим данный метод решения подробнее.

В первую очередь, определяются переменные задачи и выбирается целевая функция, то есть некоторая количественная оценка эффективности решения, позволяющая сравнивать различные варианты решения. Например, целевой функцией может являться прибыль предприятия или себестоимость затрат. Различают целевые функции на максимум (достижение наибольшего значения) и на минимум (достижение наименьшего значения). После этого добавляются ограничения задачи — условия, влияющие на возможный выбор значений переменных. Такими ограничениями могут быть запас ресурсов или спрос на определенный продукт.

Следующим шагом является поиск множества точек, которое будет удовлетворять всем ограничениям задачи. Это множество точек называется областью допустимых решений, обладающей особым свойством выпуклости, позволяющим найти решение задачи. Данная область может быть трех видов: пустой (не содержащей ни одного элемента), непустой и неограниченной, а также непустой и ограниченной. В первом случае задача не будет иметь решения, во втором будет иметь решение в зависимости от задачи (на минимум и ограничена снизу или на максимум и ограничена сверху), а в третьем будет иметь всегда. Существуют также особые вырожденные случаи области допустимых решений. Это полоса, линия, отрезок и точка. Возможный вид области допустимых решений представлен на рисунке 1 (область выделена штриховкой). Для данной области очевидно, что задача будет иметь решение в любом случае.

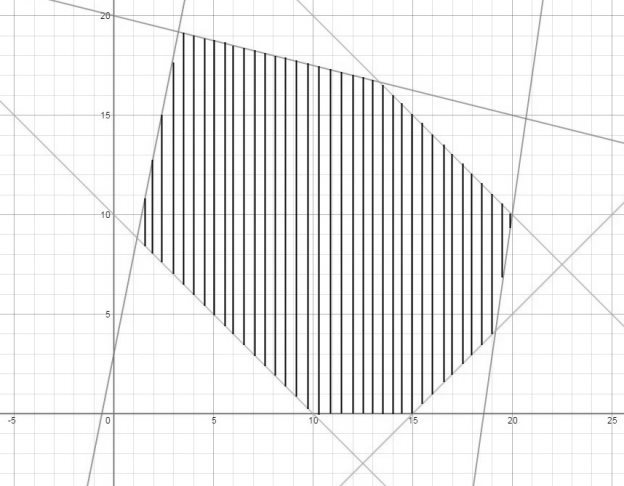
Рис. 1. Возможный вид области допустимых решений

После нахождения области допустимых решений производится поиск оптимального решения. Для этого согласно коэффициентам целевой функции строится вектор нормали, для которого рассматривается семейство прямых, перпендикулярных нормали и называемых линиями уровня. Пересечение области допустимых решений с линией уровня в том ее положении, когда дальнейшее перемещение линии уровня даст пустое пересечение (вниз для задачи на минимум и вверх для задачи на максимум), будет множеством оптимальных точек задачи линейного программирования. Разберем для примера одну из реальных управленческих задач.

Пусть компания «Оловянный солдатик» производит игрушки двух видов: из дерева и пластмассы. При этом перед выпуском игрушка проходит обработку в трех цехах. Игрушка из дерева обрабатывается два часа в первом цеху, три часа во втором цеху и один час в третьем цеху, а игрушка из пластмассы — полтора часа в первом, два часа во втором и три с половиной часа в третьем цеху. Каждый из цехов имеет свой ресурс использования в расчете на один рабочий месяц. Так, для первого цеха — это триста часов, для второго — четыреста часов, для третьего — триста пятьдесят часов. Также известно, что необходимо производить не менее десяти игрушек из дерева и не менее двадцати игрушек из пластмассы в месяц, а спрос на игрушки из дерева ограничен значением в 59 изделий. Необходимо рассчитать, сколько игрушек и какого вида может произвести компания, чтобы получить наибольшую прибыль при условии, что игрушка из дерева стоит 1500 рублей, а из пластмассы — 1000 рублей.

В первую очередь, для решения этой, кажущейся на первый взгляд непростой задачи, определяем переменные. Необходимо найти оптимальные значения производства игрушек каждого вида, поэтому именно их мы и примем за неизвестные. Таким образом, x₁ — количество (штук) игрушек из дерева, а x₂ — количество (штук) игрушек из пластмассы.

После этого определяемся с целевой функцией, то есть мерой эффективности решения. Очевидно, что в рассматриваемой задаче ей является величина прибыли, устремленная на максимум, то есть получаем: F = 1500*x₁ + 1000*x₂ → max.

Следующим этапом является составление ограничений задачи. Всего их шесть — три ограничения связаны с ресурсом цехов, два — с минимальным числом произведенных игрушек и одно — со спросом на игрушки из дерева. Данные ограничения представлены ниже:

2*x₁ + 1,5*x₂ ≤ 300;

3*x₁ + 2*x₂ ≤ 400;

x₁ + 3,5*x₂ ≤ 350;

x₁ ≥ 10;

x₂ ≥ 20;

x₁ ≤ 59.

В итоге была получена математическая модель задачи, необходимая для ее непосредственного решения. Теперь нужно найти область допустимых решений, нанеся все ограничения на координатную плоскость. В таком случае, ось абсцисс будет показывать значения переменной x₁, а ось ординат — значения переменной x₂. Полученная область допустимых решений представлена на рисунке 2.

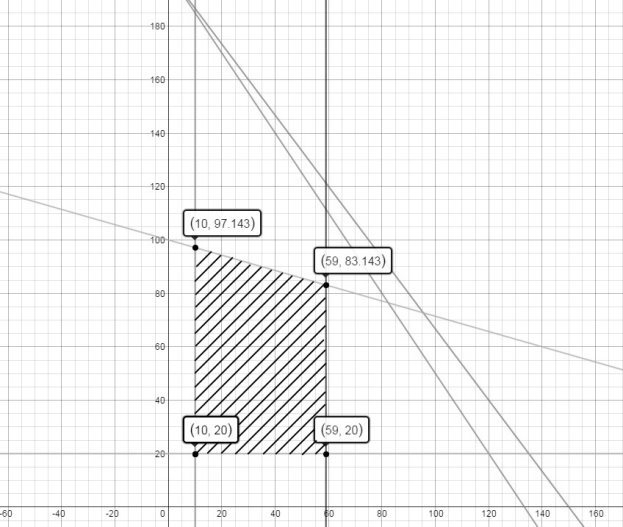
Рис. 2. Область допустимых решений

Согласно коэффициентам целевой функции получаем вектор нормали с = (1500; 1000). Для удобства возьмем вектор, сонаправленный с вектором нормали и выходящий из точки (0; 0). Это вектор q = (15; 10). Затем для этого вектора строим перпендикулярную ему прямую и откладываем вверх параллельные прямые, пока не выйдем за пределы области допустимых решений. Указанные действия представлены на рисунке 3.

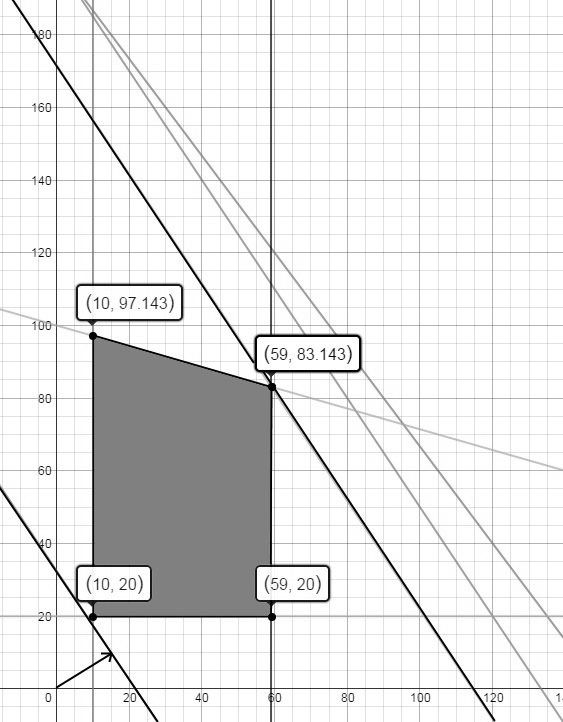
Рис. 3. Решение задачи графическим методом

Получаем, что решение находится в точке с координатами (59; 83). Так как число игрушек не может быть дробным числом, то решение находится в ближайшей точке с целыми координатами, то есть в точке (59; 83). Таким образом, необходимо произвести пятьдесят девять игрушек из дерева и восемьдесят три игрушки из пластмассы. Это позволит заработать F = 1500*59 + 1000*83 = 171500 денежных единиц.

Как видно, решение такой задачи, показавшейся первоначально довольно сложной, потребовало совсем немного времени и усилий. Зато было получено оптимальное решение, которое позволит компании заработать максимально возможное количество денег в данных условиях. Принятие управленческого решения данным способом действительно существенно повысит его эффективность, что крайне важно руководителю. Но у графического метода есть и еще одна невероятно значимая особенность — он может показать слабое место, непосредственно ограничивающее эффективность решения. Работа с таким слабым местом называется анализом решения на чувствительность [3]. Рассмотрим данную процедуру подробнее.

Оптимальное решение, чаще всего, ограничено двумя прямыми. Существуют исключительные случаи, когда через точку, в которой находится оптимальное решение, проходят несколько ограничений, но процесс в этом случае усложнится лишь тем, что нужно будет двигать дополнительное число линий. Однако вернемся к стандартному варианту с двумя прямыми, ограничивающими оптимальное решение. Именно такой случай произошел в рассмотренной задаче и наглядно показан на рисунке 3. Оптимальное решение ограничено линий спроса x₁ = 59 и ресурсом работы третьего цеха x₁ + 3,5*x₂ = 350. Данные ограничения являются сдерживающими или дефицитными. Остальные же еще имеют запас ресурса и поэтому называются недефицитными.

Анализ на чувствительность разбивается на две задачи. Первая выполняется для определения диапазона изменения коэффициентов целевой функции, при котором найденный план будет оставаться оптимальным. Так, если условно обозначить коэффициенты при целевой функции за c₁ и с₂, то исходя из сдерживающих ограничений получаем, что отношение c₁\c₂ (c₂ ≠ 0) должно лежать в диапазоне от 2/7 до бесконечности, а отношение c₂\c₁ (c₁ ≠ 0) — от 0 до 7/2. Для решения данной задачи необходимо зафиксировать один из коэффициентов и вычислить диапазон изменения второго. Например, если зафиксируем коэффициент c₁ = 1500, то коэффициент c₂ может изменяться в диапазоне от 0 до 5250, и план производства при этом не претерпит изменений.

Вторая же задача и, возможно, наиболее ценная заключается в определении того, на сколько можно увеличить запас дефицитного ресурса, чтобы целевая функция улучшилась, а также в выявлении того, какой из дефицитных ресурсов оказывает большее влияние на целевую функцию. При этом запас дефицитного ресурса увеличивается до того момента, пока хотя одно из недефицитных ограничений не станет сдерживающим. Если увеличить спрос на продукции до восьмидесяти трех единиц (округление для числа 82), то оптимальное решение окажется в точке (82; 76), как это показано на рисунке 4. На нем сдерживающее ограничение и линия уровня совпали. Соответственно, ближайшей целой точкой будет являться точка (83;75), в которой целевая функция принимает значение F = 199500. При этом отношение приращения целевой функция к приращению ресурса равно y₁ = 28000/24=1166. Если же увеличить ресурс работы третьего цеха до 449,25 часа, то оптимальное решение окажется в точке (59; 115,5), как это показано на рисунке 5. Соответственно, ближайшей целой точкой будет являться точка (59; 111), в которой целевая функция принимает значение F = 199500. При этом отношение приращения целевой функция к приращению ресурса равно y₁ = 28000/99,25=282. Таким образом, более выгодным вариантом является повышение спроса на деревянные игрушки.

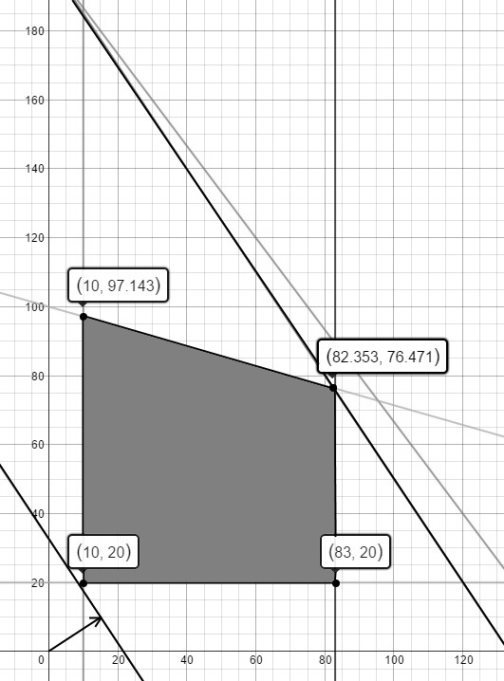
Рис. 4. Анализ увеличения спроса на деревянные игрушки

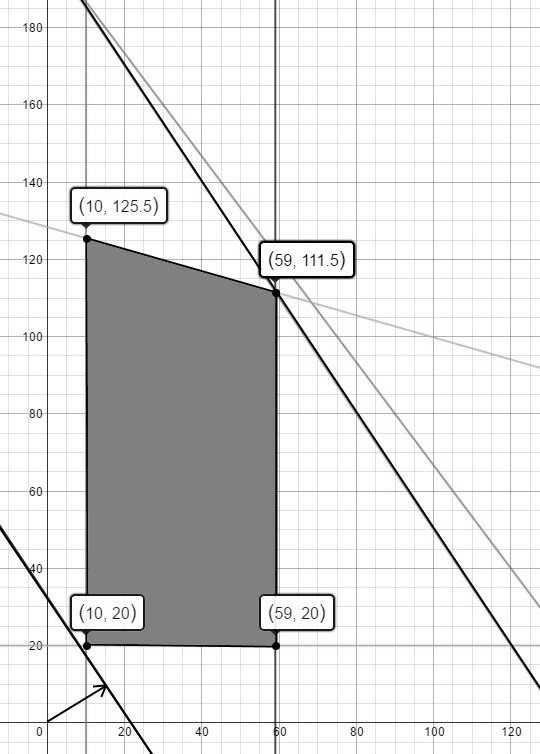
Рис. 5. Анализ увеличения ресурса работы третьего цеха

Таким образом, используя графический метод и простейшие правила анализа решения на чувствительность любой руководитель сможет принять оптимальное решение в сложившихся обстоятельствах, что существенно увеличит эффективность работы предприятия. Конечно, данный способ имеет ряд ограничений, но это никак не препятствует его использованию и принятию наиболее правильных управленческих решений.

Литература:

1. Петровский, А.Б. Теория принятия решений [Текст] / А.Б. Петровский. — М.: Издательский центр «Академия», 2009. — 400с.
2. Орлов, А.И. Теория принятия решений [Текст] / А.И. Орлов. — М.: Издательство «Март», 2004. — 656с.
3. Горемыкина, Г.И. Избранные разделы линейной алгебры с элементами экономической алгоритмики [Текст] / Г.И. Горемыкина, М.А. Ляшко. — Балашов: Издательство «Николаев», 2003. — 96с.