Пусть 
и 
-три гильбертовы пространства и 
. Тогда известно, что всякий линейный ограниченный оператор 
, действующий в 
всегда представляется как 
блочно-операторная матрица
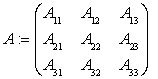(1)
с линейными ограниченными операторами 
. При этом оператор 
является самосопряженным тогда и только тогда, когда
(
сопряженный оператор к 
).
Пространство 
представим в виде ортогональной суммы гильбертовых пространств 
и 
. Положим
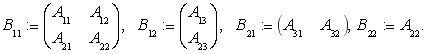
Очевидно, что 
Тогда оператор 
действующий в 
относительно представление 
записывается как блочно-операторная матрица [1] следующего вида:
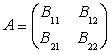(2)
Пусть 
- множество комплексных чисел и 
- пространство линейных ограниченных операторов в гильбертовом пространстве 
. Следующие операторы
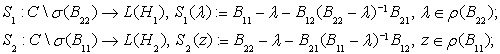
называются дополнениями Шура соответствующий блочно-операторной матрицы 
, определенный по формуле (2) и они играют важную роль в спектральном анализе этой матрицы [1–3]. Видно, что дополнение Шура являются операторно-значные регулярные функции определенные вне спектров операторов 
и 
, соответственно.
Пусть 
— 
-мерный куб с соответствующим отождествлением противоположных граней, 
- гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на 
. Рассмотрим случай, когда 
и 
. Пространства 
и 
называются нольчастичным, одночастичным и двухчастичным подпространством стандартного фоковского пространства 
по 
.
Всюду в работе будем рассматривать блочно-операторную матрицу 
, определенную по формуле (1), со следующими матричными элементами
Здесь 
-фиксированное вещественное число; 
и 
- вещественно-непрерывные функции на 
и 
, соответственно. При этом
.
Можно легко проверить, что при этих предположениях блочно-операторная матрица 
является ограниченным и самосопряженным оператором в 
.
Простые вычисления показывают, что первое дополнение Шура
блочно-операторной матрицы 
(действующее по формуле (2)) соответствующее разложению 
определяется следующим образом
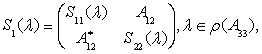
где
При каждом фиксированном 
определим регулярную в 
функцию
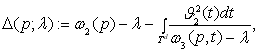
где числа 
и 
определяются следующим образом:
Тогда 
есть оператор умножения на функцию 
Следует отметить, что при каждом фиксированном 
оператор типа (3) является оператором, носящим название обобщенной модели Фридрихса.
Пусть
Следующая теорема описывает существенный спектр оператора
.
Теорема. При каждом фиксированном 
для существенного спектра оператора 
имеет место равенство
.
Доказательство. Очевидно, что операторы 
, 
и 
, 
являются самосопряженными операторам ранга 1. Из известной теоремы Вейля [4] о сохранении существенного спектра при возмущениях конечного ранга следует, что существенный спектра оператора 
совпадает с существенным спектром оператора 
. Из непрерывности функции 
при 
на компактном множестве 
следует следующая теорема 
. Отсюда вытекает, что 
. Теорема доказана.
Литература:
- C. Tretter. Spectral Theory of Block Operator Matrices and Applications. Imperial College Press, 2008.
- I. Schur. Uber potenzreihen, die im innern des einheitskreises beschrankt sint. J. Reine Angew. Math., 147 (1917), 205–232.
- F. Zhang. The Schur complement and its applications. Vol. 4 of Numerical Methods and Algorithms. Springer, New York, 2005.
- М. Рид, Б. Саймон. Методы современной математической физики. Т. 4. Анализ операторов. –М.: Мир. 1982, –430 С.
