Блочно-операторная матрица — это матрица, элементы которой являются линейными операторами в банаховом или гильбертовом пространствах [1]. Одним из специальных классов блочно-операторных матриц являются Гамильтонианы системы с несохраняющимся числом квантовых частиц на целочисленной решетке. Их количество может быть неограниченным, как в случае моделей спин-бозонов [2,3] или ограниченным, как в случае урезанных моделей спин-бозонов [4,5].
В настоящей заметке рассматривается матричный модель 
, ассоциированный с системой, описывающий два одинаковых фермионов и одной частицы иной природы, взаимодействующих с помощью операторов рождения и уничтожения. Описан местоположение существенного спектра оператора 
через спектр обобщенной модели Фридрихса 
, т. е. выделены двухчастичная и трехчастичная ветви существенного спектра оператора 
и установлено, что существенный спектр состоит из объединения не более, чем трех отрезков.
Через 
обозначим 
-мерный куб с соответствующим отождествлением противоположных граней. Пусть 
одномерное комплексное пространство, 
гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на 
, 
гильбертово пространство антисимметричных функций двух переменных, определенных на 
и 
стандартное фермионное пространство Фока над 
.
Положим
; 
.
Пространство 
называется “двухчастичным обрезанным” подпространством пространства 
. В настоящей работе исследуем модели соответствующих случаев 
. Для удобства положим
, 
, 
.
В гильбертовом пространстве 
рассмотрим следующую блочно-операторную матрицу
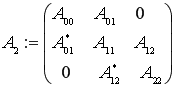(1)
с матричными элементами 
, 
, 
:
;
;
.
Здесь 
- фиксированное вещественное число, 
и 
- вещественнозначные непрерывные функции на 
, а 
— «параметр взаимодействия».
В этих предположениях на параметры оператор 
, действующий в гильбертовом пространстве 
по формуле (1) является ограниченным и самосопряженным. При этом 
сопряженный оператор к 
, 
и
.
Операторы 
и 
называются операторами уничтожения, а 
и 
называются операторами рождения
С целью изучения спектральных свойств оператора 
нарядус этим оператором рассмотрим еще один ограниченныйсамосопряженный оператор 
(обобщенная модель Фридрихса),который действует в 
как 
блочно-операторные матрицы
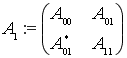
Заметим, что в операторе 
индекс 
означает возможное число фермионов в рассматриваемой системе.
Сначала напомним, что для 
и 
имеет место равенство
.
Обозначим
.
.
При этом надо отметить, что
Поэтому имеет место равенство
.
Основной результат настоящей работы является следующая теорема.
Теорема. Существенный спектр оператора 
совпадает с множеством 
, т. е. 
. Более того, множество 
представляет собой объединение не более чем трех отрезков.
Литература:
- C. Tretter. Spectral Theory of Block Operator Matrices and Applications. Imperial College Press, 2008.
- H. Spohn. Ground states of the spin-boson Hamiltonian // Comm. Math. Phys., — 1989, — V. 123, — P. 277–304.
- M. Huebner, H. Spohn. Spectral properties of the spin-boson Hamiltonian // Ann. Inst. HenriPoincare, — 1995, — V. 62, — no. 3, — P. 289–323.
- Ю. В. Жуков, Р. А. Минлос. Спектр и рассеяние в модели «спин-бозон» с не более чем тремя фотонами // Теор. и матем. физика, — 1995, — Т. 103, — № 1, — С. 63–81.
- R. A. Minlos, H. Spohn. The three-body problem in radioactive decay: the case of one atom and at most two photons // Topics in Statistical and Theoretical Physics, American Mathematical Society Translations-Series 2, — 1996, V. 177, — P. 159–193.
- С. Н. Лакаев, Т. Х. Расулов. Модель в теории возмущений существенного спектра многочастичных операторов // Математические заметки. — 2003, — Т. 73, — № 4, — С. 556–564.
- S. Albeverio, S. N. Lakaev, T. H. Rasulov. On the Spectrum of an Hamiltonian in Fock Space. Discrete Spectrum Asymptotics // Journal of Statistical Physics. — 2007, — V. 127, — no. 2, — P. 191–220.
- Т. Х. Расулов. О структуре существенного спектра модельного оператора нескольких частиц // Математические заметки. — 2008, — Т. 83, — № 1, — С. 78–86.
