Рассмотрена задача кинематического анализа рычажного механизма. Определены возможности использования пакетов прикладных программ Mathcad и MSCADAMS для кинематического исследования кривошипно-шатунного механизма.
Ключевые слова: рычажный механизм, кривошипно-шатунный механизм, кинематический анализ.
В настоящее время во многих машинах применяются рычажные механизмы, состоящие из жестких звеньев, соединенных между собой кинематическими парами V класса. Кинематическое исследование такого механизма предусматривает изучение движения звеньев и их особых точек без учета действующих на механизм сил. Задачи кинематики могут быть решены графическим, графоаналитическим и аналитическим методами [1]. Первые два из них используются, главным образом, в учебных целях. Аналитический метод исследования позволяет получить точное решение. Однако непосредственное решение для определения функций положения, скоростей и ускорений приводит к громоздким уравнениям, решение которых порой сопряжено с чрезмерными затратами времени и высокой вероятностью ошибки.
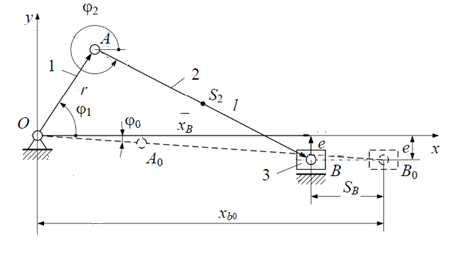
Рассматриваемое устройство представляет собой кривошипно-шатунный механизм, состоящий из шарнирно соединённых звеньев (кривошип ОА длиной l = 0.28 м, шатун AB длиной r = 0.09м и ползун С) (рис.1). Кривошип вращается с постоянной угловой скоростью ω1 = 12 рад/с. Неподвижная система координат имеет начало координат в неподвижном шарнире О. Ось координат x направлена параллельно траектории движения ползуна 3, которая смещена относительно начала координат вдоль оси координат y на расстояние e = 0.05 м. Угол поворота кривошипа ![]() отсчитывается от оси x против часовой стрелки. Начальным считается положение механизма, при котором ползун занимает крайнее правое положение и определяется углом
отсчитывается от оси x против часовой стрелки. Начальным считается положение механизма, при котором ползун занимает крайнее правое положение и определяется углом ![]()
Угол поворота шатуна является функцией угла поворота кривошипа
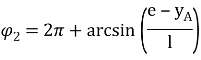 (1)
(1)
|
|
|
Рис. 1 — Схема кривошипно-ползунного механизма |
Координата шарнира В по оси x определяется выражением
![]() (2)
(2)
Дифференцированием выражения (1) определяются скорости и ускорения ползуна.
Координаты центра тяжести шатуна
![]() (3)
(3)
![]() (4)
(4)
Скорости и ускорения этой точки определяются дифференцированием выражений (3) и (4).
Величина перемещения ползуна составляет
![]() (5)
(5)
В настоящее время для исследования кинематики рычажных механизмов эффективно используют различные готовые программные продукты. Большое распространение получила система MathCAD, которая позволяет рассчитать координаты звеньев рычажных механизмов в зависимости от изменения угла ведущего звена с любым шагом. Система встроенных функций Mathcad позволяет вычислить скорости и ускорения особых точек рычажных механизмов, что даёт возможность рассчитать траектории заданных точек механизмов [2,3].
Пакет прикладных программ MSC.ADAMS предназначен для создания, тестирования и оптимизации работы моделей механизмов и конструкций, состоящих из абсолютно твердых тел и их соединений [4]. Основной базовый пакет модулей MSC.ADAMS, дающий возможность собирать и анализировать модели, сложность которых ограничивается в основном возможностями компьютера, распространяется на льготных условиях для некоммерческого использования в университетах [4].
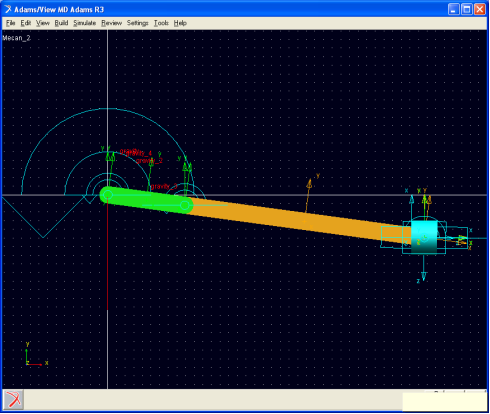
Моделирование кривошипно-шатунного механизма проведено с помощью модуля ADAMS/View (рис. 2). Он позволяет анализировать кинематику и динамику систем тел, находящихся под действием внешних задаваемых сил и реакций внешних и внутренних связей.
|
|
|
Рис. 2 — Модель кривошипно-шатунного механизма в MSC.ADAMS |
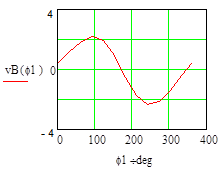
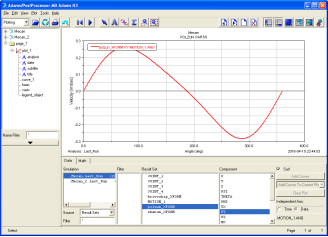
Проведено сравнение результатов расчёта программы MathCAD и модуля ADAMS/View, а также было выполнено графическое исследование. На рис. 3–5 показано сравнение кинематических характеристик кривошипно-шатунного механизма: скорости (рис. 3) и ускорения (рис. 4) ползуна; скорости (рис. 5) центра масс шатуна в зависимости от угла поворота кривошипа.
|
|
|
|
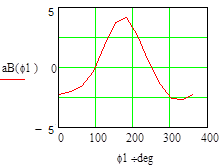
Рис.3 — Скорости ползуна в зависимости от угла поворота кривошипа, вычисленные в программах MathCAD и MSC.ADAMS |
|
|
|
|
|
|
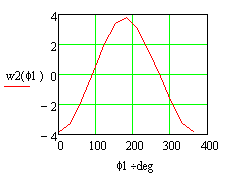
Рис. 4 — Ускорения ползуна в зависимости от угла поворота кривошипа, вычисленные в программах MathCAD и MSC.ADAMS |
||
|
|
|
|
|
Рис. 5 — Скорости центра масс шатуна в зависимости от угла поворота кривошипа, вычисленные в программах MathCAD и MSC.ADAMS |
||
При сравнении кинематических характеристик видно хорошее совпадение результатов расчёта, выполненное в разных программах.
Модуль ADAMS/View обладает большими возможностями, но в то же время является и более сложным в изучении. Он позволяет проводить уточнённые расчёты с учётом трения и деформаций и исследовать реальные модели. Поэтому при проектировочных расчётах несложных моделей удобнее и проще пользоваться программой MathCAD, а для выполнения кинематического и динамического анализа сложных моделей целесообразно использовать MSC.ADAMS.
Литература:
- Артоболевский И. И. Теория механизмов и машин: — М.: «Наука», 1988–640с.
- Котлярский Л. Н. MathСad. Решение инженерных и экономических задач / Л. Н. Котлярский. — СПб.: Питер. — 2005. — 388 с.
- Эйзеншпис А. А. MathСad 2000. Руководство пользователя / А. А. Эйзеншпис. — М.: ДМК Пресс. — 2001. — 570 с.
- Иванов А. А. MSC.ADAMS: теория и элементы виртуального конструирования и моделирования: Учебное пособие / А. А. Иванов — М.: Московское представительство MSC.Software GmbH, 2003. 97 с.