Существует множество функционально и пространственно распределенных структур, для которых характерно наличие пространственной компоненты. Эти структуры отличаются функциональным назначением и набором других характеристик. Статья анализирует модели сжатия геометрической информации на основе нечеткой логики.
Ключевые слова: математическая модель, нечеткая логика, пространственное распределение.
There are many functionally and spatially distributed structures, which are characterized by the presence of the spatial component. These different structures and functionality of the set of other characteristics. The article analyzes the model geometry information compression based on fuzzy logic.
Keywords: mathematical model, fuzzy logic, spatial distribution.
Постановка задачи. Необходимость оценки состояний пространственно-распределенных объектов существует во многих отраслях народного хозяйства, однако наличие значительных объемов информации, которая характеризуется неопределенностью, нечеткостью, вызывает необходимость дальнейших исследований для повышения достоверности оценивания состояний объектов. Это, как известно, вызывает значительные трудности в определении критериев и технологий.
Постановка задачи исследования. Рассмотрим множество пространственно распределенных объектов (1).
![]() (1)
(1)
где OSp — пространственно распределенные объекты земельных ресурсов; T S — объекты транспортных систем; OI — распределенные объекты промышленного назначения; O In — распределенные объекты инфраструктуры; FR — факторы ресурсного обеспечения.
Характерными объектами могут быть пространственно распределены земельные ресурсы, транспортные системы, распределенные объекты промышленного назначения. Оценка состояний таких объектов является важной и актуальной проблемой.
Исходя из особенностей предметной области исследования, построим знания-ориентированную модель для множества пространственно распределенных объектов (2)
учитывающей детерминизм объекта, вероятностные характеристики и показатели нечеткости.
Анализ и модификация досягаемости процессов на модели. Изложенная процедура в ряде случаев имеет свойства отсутствии досягаемости и наличии конфликтных ситуаций на этапах анализа. Это потребовало содержательного анализа и возможной модификации моделей [3] по критериям досягаемости 1, 2, 3, 4, упорядоченных по степени сложности анализа [3] и критериям поиска конфликтных ситуаций на множестве решений [3].
Используя научные положения статьи [5], представим сетевую модель [2], которая отражает детерминированную сущность структуры модели в виде (2). Для обобщенной технологии [3] (рис. 1), построим сетевую модель (рис. 2) и осуществим ее содержательный анализ в программной среде FPN [9], предназначено для моделирования и анализа процессов с помощью МП.
На рис. 1 представлены:
П — начало выполнения технологии;
Α1-Α4 — операторы реализации обобщенной технологии;
Β1-Β2 — операторы построения нормативной базы и обучения модели объекта;
В — логический оператор выполнения условий обучения модели объекта;
Κ — окончание выполнения технологии.
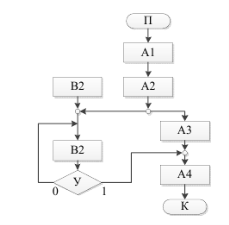
Рис. 1. Обобщенная структура технологии
Анализ состояний был реализован в среде FPN [9] при матричном нечетком отображении нечетких процессов анализа [3]
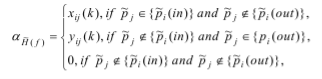 (3)
(3)
где xij (k), yij (k) — множества функций принадлежности входных и выходных дуг модели.
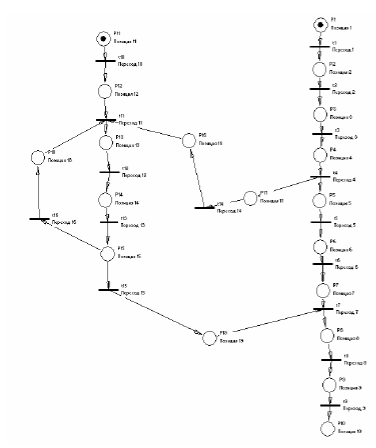
Рис. 2. Сетевая модель
Модифицированная обобщенная структура технологии приведена на рис. 2.
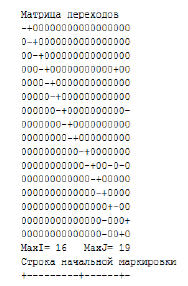
Проверка модифицированной сетевой модели (рис. 2) на наличие конфликтов показала отсутствие конфликтов. Проверка модифицированной сетевой модели (рис. 2) на наличие досягаемости принятия решений по четырем критериям [3] показала наличие досягаемости принятия решения по всем критериям.
В сетях Петри различают переходы пяти типов (рис. 3). Переход t j ∈T в маркированной МП с маркировкой Mpi может быть запущен всякий раз, когда его разрешено. Это происходит, когда для всех pi ∈ P справедливо![]() [2].
[2].
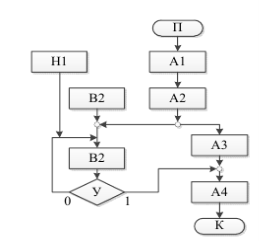
Рис. 3. Модифицированная обобщенная структура технологии
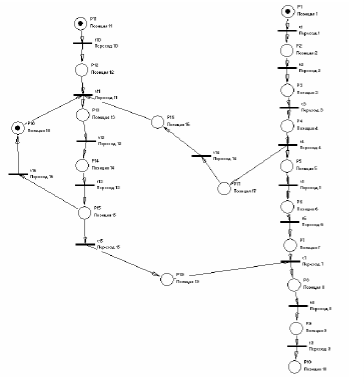
Рис. 4. Сетевая модифицированная модель
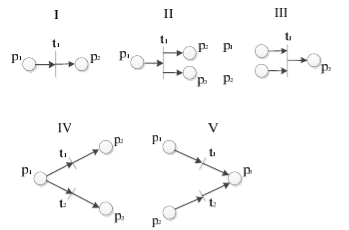
Рис. 5. Типы переходов в МП
Используя правила выполнения переходов на типах переходов (рис. 5) исследователь имеет возможность конструировать рациональную структуру моделей процессов на сетях Петри.
Особенностью существующих структур, построенных с помощью нечетких МП [5], является возможность подачи нечетких процессов и динамики их взаимодействия. К недостаткам таких систем относят отсутствие возможности учета множества параметров, показателей и характеристик, без которых сложно представить реальные процессы практических реализаций. Кроме этого, ограниченная возможность задания показателей нечеткости маркировок и компонент функции инцидентности, что существенно ограничивает возможности исследователя.
Необходимо исследовать основные подходы к синтезу нечетких алгоритмов и моделей, построения нечетких отношений, композиции фрагментов моделей и алгоритмов при реализации нечетких алгоритмов на основе расширенных классов интервальных МП — нечетких интервальных интегрированных цветных сетей Петри (НИИКМП).
Представление МП изображено на рис. 6 [6], где позиция p1 есть входным условием для перехода t, а p2 — исходным условием.
Неформально работу сети можно представить, как совокупность сработавших переходов на множестве инциденций F.
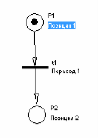
Рис. 6. Элементарная МП
Для ординарной МП (то есть сети, в которой дуги имеют кратность равную единицы и отсутствуют предикаты на выполнение переходов) условие срабатывания перехода означает, что любая входная позиция этого перехода имеет хотя бы один маркер (рис. 7, а) [6], то есть имеет ненулевое значение маркировки.
Срабатывания разрешенного перехода t приводит к изменению маркировки: маркер, находился в позиции p1 (рис. 7, а) [6] в результате срабатывания перехода перемещается в позицию p2 (Рис. 7, б) [6].
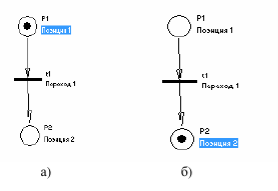
Рис. 7. Срабатывание перехода в элементарной МП 73
Когда же переход связан со своими позициями кратными дугами, правило срабатывания перехода звучит так: при срабатывании перехода t он убирает с каждой своей входной позиции столько маркеров, сколько дуг связывает этот переход с указанием позиции, и добавляет в каждую свою исходную позицию количество маркеров равную кратности дуг, которые связывают (Рис. 8, а и б) [6].
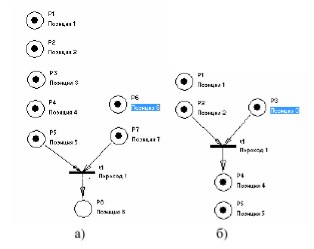
Рис. 8. Срабатывание перехода при неординарной МП
МП отражают отношение «условие — действие», которые могут носить нечеткий характер. Рассмотрим подходы к решению проблем, связанных с проявлением и устранением нечеткости, а также неопределенности исходных данных.
Под неопределенностью нечетких исходных данных будем понимать отсутствие их принадлежности μA~(x)=0 до множества значений БЗ, определяют исходное состояние сложного объекта.
Пусть имеется множество исходных данных:
Если исходные данные характеризуются неопределенностью, то:
![]() (5)
(5)
где ID~i — множество начальных данных, 1≤i≤n; Azj — Множество значений антецедентов правил продукции БЗ:
![]() (6)
(6)
где μID~i(k0)* — предельно допустимое значение соответствующей функции для (6).
Учитывая сложное взаимодействие процессов, для решения задачи определение значения ID~i с применением (5) и (6) целесообразно применить модификацию и развитие нечетких МП [6]. Необходимость модификации существующей версии нечеткой интервальной МП [6] вызвана тем, что в данной работе используются в явном виде только значение функций принадлежности, а не их аналитическая форма. Это вызывает соответствующие осложнения использования результатов работы [6] в процедурах нечеткого логического вывода.
Так, в работах [4, 5] определены интеллектуальные механизмы моделирования динамики нечетких процессов классами интервальных МП, что является основой модификации моделей и сетей. Интеллектуальные механизмы основаны на представлении и интерпретации фрагментов нечетких алгоритмов классами интервальных МП и моделировании процессов в нечетком пространстве состояний модели, которые являются теоретической базой решения прикладных задач.
Большинство понятий повседневной жизни не укладываются в рамки традиционной бинарной логики. Попытка представить такие понятия по помощью конкретных числовых рамок или недопустимо опишут в предметной области, или чрез меру усложнят решение задачи. Нечеткая логика предлагает более элегантное решение для подобных ситуаций. В процессе работы возникла необходимость описания качественных понятий «плохо», «хорошо», «сильно», «умеренно» некоторой функцией распределения и использовать их как точные, не волнуясь больше о «нечеткой» природе [1]. Теория нечеткой логики позволяет выполнять над такими величинами весь спектр логических операций [9, 6]: объединения, пересечения, отрицания и другие.
Выводы. Таким образом, в работе рассмотрены особенности интервальных представлений, которые базируются на основных логических операциях над нечеткими множествами и могут быть полезными в дальнейших исследованиях при анализе моделей.
Литература:
- Глушков В. М. Моделирование развивающихся систем [Текст] / В. М. Глушков, В. В. Иванов, В. М. Яненко. — М.: Наука, 1983. — 350 с.
- Вейцман К. Распределенные системы мини- и микроЭВМ [Текст] / К. Вейцман. — М.: Финансы и статистика, 1983. — 362 с.
- Миков А. И. Распределенные системы и алгоритмы [Электронный ресурс] / А. И. Миков, Е. Б. Замятина. — Режим доступа: http://www.intuit.ru/department/algorithms/distrsa/1/.
- Кельтон В. Имитационное моделирование. Классика CS [Текст] / В. Кельтон, А. Лоу. — СПб.: Питер: Киев: Издательская группа BHV, 2004. — 847 с.
- Бусленко Н. П. Моделирование сложных систем [Текст] / Н. П. Бусленко. — М.: Наука, 1978. — 399 с.
- Бодянский Е. В. Нейро-фаззи сети Петри в задачах моделирования сложных систем [Текст] / Е. В. Бодянский, Е. И. Кучеренко, А. И. Михалев. — Дніпропетровськ: Системні технології, 2005. — 311 с.
- Борисов В. В. Нечеткие модели и сети [Текст] / В. В. Борисов, В. В. Круглов, А. С. Федулов. — М.: Горячая линия — Телеком, 2007. — 284 с.
- Питерсон Дж. Теория сетей Петри и моделирование систем [Текст] / Дж. Питерсон — М.: Мир, 1984. — 264 с.
- Гаврилова Т. А. Базы знаний интеллектуальных систем [Текст] / Т. А. Гаврилова, В. Ф. Хорошевский. — СПб: Питер, 2000. — 384 с.
- Творошенко И. С. Об интеллектуальных средствах принятия решений в сложных системах [Текст] / И. С. Творошенко // Искусственный интеллект. Интеллектуальные и многопроцессорные системы — 2004: Материалы междунар. науч.-техн. конф., Таганрог — Донецк, сентябрь 2004 г. — Донецк: Искусственный интеллект, 2004. — Т. 2. — С. 226–229.
- Творошенко И. С. Информационные технологии в задачах компьютерной диагностики с использованием интеллектуальных систем [Текст] / И. С. Творошенко, А. П. Дехтярь // Клиническая информатика и Телемедицина. Компьютерная Медицина — 2005: материалы междунар. научн.-технич. конф., Харьков, июнь 2005 г. — Х.: ХНУРЭ, 2005. — Т. 2, № 1. — С. 138.
- Кучеренко Е. И. Об информационных технологиях принятия решений в задачах оценки состояния территорий [Текст] / Е. И. Кучеренко, И. С. Глушенкова // Искусственный интеллект. — 2010. — № 3. — С. 489–493.







