Модели многих задачи прикладного характера сводятся к уравнением [2], среди которых неклассические уравнения представляют особые интересы и мало изучены. В данной работе построено регуляризирующее уравнение для неклассического интегрального уравнения Вольтерра I рода в пространстве непрерывных функций с условием Липшица [6].
Models of many problems of applied nature are reduced to the equation [2], including non-classical equations of special interest and are poorly understood. In this paper we built a regularizing equation for non-classical Volterra integral equation of type I in the space of continuous functions with Lipchitz condition [6].
Расмотрим интегральное уравнение
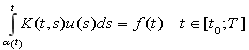 (1)
(1)
где ![]() при всех
при всех ![]()
![]() и
и ![]() известные фунции в области
известные фунции в области ![]() и на отрезке
и на отрезке ![]() соответственно
соответственно ![]()
Уравнение вида (1) возникает при решении многих прикладных задач [2], [4]. Однако, уравнения такого типа значительно менее исследованы, чем классические уравнения Вольтерра I рода.
В данной работе в предположении ![]() следуя по методу предположенному М. Иманалиевым и А. Асановым [1] строится регуляризация (1) в ппространстве непрерывных функций.
следуя по методу предположенному М. Иманалиевым и А. Асановым [1] строится регуляризация (1) в ппространстве непрерывных функций.
Следуя по методике предложенный в [1]- [4] и развитат в [5] строим регуляризация уравнение для (1).
Лемма 1. (Обобщенная формула Дирихле). Пусть
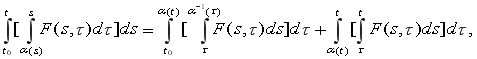
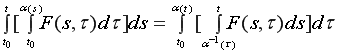 где
где ![]() обратная функция к
обратная функция к ![]()
Доказательство. Доказательство вытекает из следующего графика:
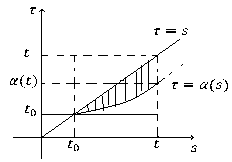
Предполагаем выполнение следующих условий
10 ![]()
![]() при почти всех
при почти всех ![]()
20 ![]() и
и ![]() при всех
при всех ![]()
30 Функция ![]() удовлетворяет условию Липщица по
удовлетворяет условию Липщица по ![]() т. е.
т. е. ![]() и при всех
и при всех ![]()
![]()
![]() - const.
- const.
Наряду с уравнением (1) рассмотрим уравнение
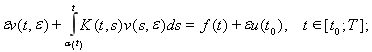 (2)
(2)
где, ![]() - решение уравнения (1).
- решение уравнения (1).
Его решение будем искать в виде
Тогда из (2) имеем ![]() .
.
Последнее перепишем в следующем виде
![]() (4)
(4)
Используя резольвенту ядра ![]() из (4) получим
из (4) получим
![]()
![]()
Из последнего переходим
![]()
![]()
![]() (5)
(5)
Применим обобщенную формулу Дирихле и преобразуем двойные интегралы в (5):
![]()
![]() (6)
(6)
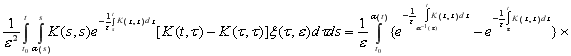
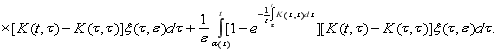 (7)
(7)
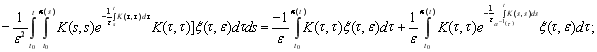 (8)
(8)
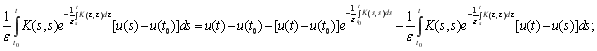 (9)
(9)
В силу (6)-(9) уравнение (5) примет вид
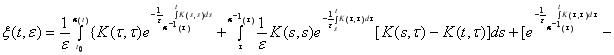
![]()
![]()
![]() (10)
(10)
![]() Введем обозначения
Введем обозначения
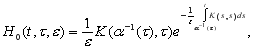 (11)
(11)
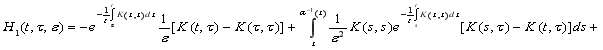
![]() (12)
(12)
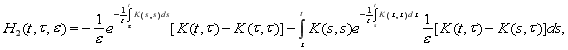 (13)
(13)
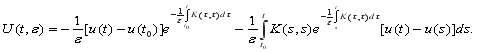 (14)
(14)
Учитывая обозначения (11)-(14) уравнение (10) запишем в следующем виде
![]()
![]() (15)
(15)
Далее нам понадобится следующая лемма.
Лемма 2. Пусть выполняются условия 10- 30 и функции ![]()
![]() и
и ![]() определены формулами (11), (12) и (13) соответственно. Тогда справедливы следующие оценки:
определены формулами (11), (12) и (13) соответственно. Тогда справедливы следующие оценки:
1) ![]() (16)
(16)
где ![]()
2)![]() (17)
(17)
3)![]() (18)
(18)
Доказательство. 1) Учитывая (11) и сделав подстановку ![]() имеем
имеем
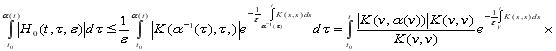
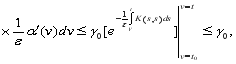
![]()
2) Учитывая условия
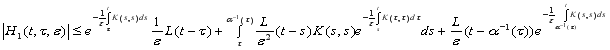
Отсюда, интегрируя по частям, имеем
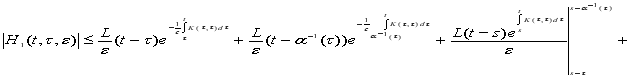
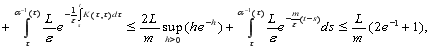
![]()
3) Учитывая условия 20 и 30, интегрируя по частям, из (13) имеем
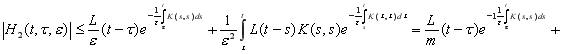
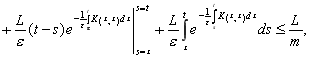
![]()
Лемма 2 доказана.
Лемма 3. Пусть выполняются условия 20 и ![]() определена по формуле (14). Тогда:
определена по формуле (14). Тогда:
Если ![]() то
то
![]()
![]() (19)
(19)
где
Доказательство: Пусть ![]()
![]() Тогда из (14) имеем
Тогда из (14) имеем
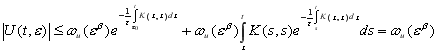 (20)
(20)
Если ![]() то
то
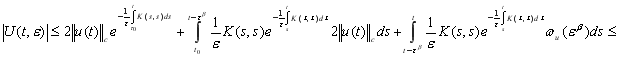
![]() (21)
(21)
Из оценки (20) и (21) вытекает оценка (19).
Лемма 3 доказана.
Теорема 1. Пусть выполняются условия 10–30 и ![]() где
где ![]()
![]() Тогда: если уравнение (1) имеет решение
Тогда: если уравнение (1) имеет решение ![]() то решение
то решение ![]() уравнения (2) при
уравнения (2) при ![]() сходится по норме
сходится по норме ![]() к решению
к решению ![]() . При этом справедлива оценка
. При этом справедлива оценка
![]() (22)
(22)
где ![]()
Доказательство. В силу оценки (16), (17), (18) из уравнения (15), имеем
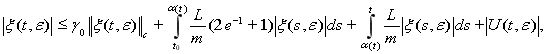
Отсюда имеем
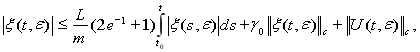
![]() (23)
(23)
Применяя неравенство Гронуолла-Беллмана, из (23) имеем
![]()
Отсюда вытекает
![]() (24)
(24)
В силу оценки (19), из (24) получим требуемые оценки (22). Теорема 1 доказана.
Литература:
- Лавреньтев М.М. Об интегральных уравнениях первого рода //ДАН. 1959. Т. 127. № 1. С. 31-33.
- Апарцин А.С. Неклассические упавнения Вольтера I рода. Теория и численные методы.
- Глушков В.М., Иванов В.В., Яненко В.М. Моделирование развивающихся систем. –М.: Наука 198-350 с.
- Иманалиев М.И., Асанов А. О решениях систем нелинейных интегральных уравнений Вольтерра первого рода // ДАН 1989. Т. 309. № 5. С. 1052-1055.
- Иманалиев М.И., Асанов А. Регуляризация и единственность решений систем нелинейных интегральных уравнений третьего рода // ДАН 2007. Т. 415. № 1. С. 14-17.
- Иманалиев М.И., Асанов А. Регуляризация, единственность и существование решения для интегральных уравнений первого рода //Исслед. по интегро-дифференц. уравнениям.-Фрунзе: Илим 1988,-вып.21-С.3-38.
- Асанов А., Бекешов Т.О., Чоюбеков С.М. Регуляризация и единственность решения неклассического интегрального уравнения с условием Липшица// Спец. выпуск, Вестник КНУ 2011. стр. 108-122.
- Асанов А., Бекешов Т.О., Чоюбеков С.М. О решении неклассического интегрального уравнения I рода в пространстве непрерывных функции// Вестник ОшГУ-3 2012. стр. 48-54.
- Асанов А., Бекешов Т.О., Чоюбеков С.М. Об одном классе неклассического интегрального уравнения вольтерра I рода// Вестник ОшГУ-3 202. стр. 83-88.







