Определение оптимальных алгоритмов управления фильтрационными системами
Жакбаров Одилжон Отамирзаевич, кандидат технических наук, доцент;
Комилов Сахоб Расулжонович, ассистент, старший преподаватель;
Наманганский инженерно-педагогический институт (Узбекистан)
Холмирзаев Хошимжон Эркинжонович, ассистент
Наманганский государственный университет (Узбекистан)
Жакбарова Дилноза Хабибуллаевна, заведующая кафедрой, преподаватель
Наманганский профессиональный колледж строительства и дизайна (Узбекистан)
Важной целью определения оптимальных алгоритмов управления фильтрационными системами является отыскание наиболее быстрых и экономически выгодных методов решения, т. е. оптимизация вычислительных алгоритмов. Проблему определения оптимальных алгоритмов решения при заданных ограничениях необходимо изучать с помощью общих математических теорем и оценивать минимально возможные затраты на решение конкретной задачи из заданного класса или суммы задач [1].
Рассмотрение одной изолированной математической задачи для определения оптимальных алгоритмов большей частью не решает практического вопроса. Однако, умея находить наилучший способ решения при заданных возможностях и средствах вычислений каждой локальной задачи, мы тем самым подходим к решению общей проблемы.
В процессе исследования сложных систем объектов добычи газа приходится решать различные по постановке и характеру задачи, среди которых наиболее важными являются определения задачи оптимальных алгоритмов управления.
Одними из важных оптимизационных задач сложных систем объектов добычи газа являются:
обеспечение максимальной добычи газа;
достижение минимальной себестоимости газа;
обеспечение максимальной эффективности капиталовложений;
оптимальное распределение общих производственных заданий по различным производственным объектам и др.
Сложность объектов добычи газа, обусловленная многообразием технологических процессов, а также большим числом составляющих их элементов, приводит к необходимости проведения синтеза и классификации рассматриваемых задач.
При решении таких задач необходимо учитывать их функциональные, динамические и конструктивные связи с системой (объектом), к которой они относятся.
Для определения оптимальных алгоритмов управления фильтрационных систем используются методы конечных разностей. Широкое использование метода конечных разностей для решения дифференциальных уравнений математической физики вызывает необходимость детального изучения всех свойств разностных схем. Такими свойствами прежде всего являются устойчивость и сходимость.
Для определения оптимального алгоритма в качестве примера рассмотрим однородный пласт прямоугольного вида 0х1000 м, 0y1000 м, на контуре которого задается начальное давление. В центре области расположена одна добывающая скважина с постоянным дебитом Q=150 м3/сутки.
Характеристика пласта: начальное давление Р0=150 кгс/см2, проницаемость К=0,07=const Дарси, пористость М=0,01=const, эффективная мощность h=10 м, число технологических скважин N=1, срок разработки Т=7 год, длина пласта Lx=1000 м, ширина пласта Ly=1000 м, динамическая вязкость µ=1 спз, абсциссы и ординаты скважин (ОХ=51, ОУ=51), число узлов по 0Х равно Nх=101, число узлов по 0У равно Ny=101, шаг по времени t=30 сут. Требуется определить изменение давления по времени.
Для проверки достоверности полученных результатов решаем следующую задачу с теми же исходными данными для =0 и
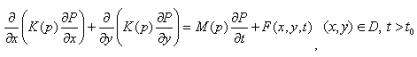 (1)
(1)
Начальные условия: ![]()
В общем случае на границе области задается условие:
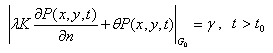 (2)
(2)
Наша основная задача — определить оптимальный алгоритм на основе полученных результатов. Поэтому для ее решения задачи будем применять все приведенные выше методы.
В табл. 1 приведены результаты, полученные с помощью методов расщепления. В этом таблице номер скважины № =5. Расчеты продолжались до T=7 лет, а все полученные результаты приведены на временном шаге t=360.
Во всех методах расчетные значения изменились немного на каждом временном шаге. Это указывает на то, что точность методов очень чувствительна на временном шаге.
При рассмотрении каждого метода на всех таблицах замечаем, что значения результатов изменились незаметно. Для проверки результата построим график на основе табл. 1
Таблица 1
Полученные результаты c помощью методов расщепления
|
Методы |
№скв |
ОХ |
ОУ |
Годы |
Время счета на ЭВМ |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Метод переменных направлений |
5 |
51 |
51 |
147.194 |
146.883 |
145.685 |
144.371 |
144.371 |
143.174 |
142.411 |
15 сек. |
|
Метод покомпонентного расщепления |
5 |
51 |
51 |
147.849 |
146.747 |
145.857 |
145.033 |
144.235 |
143.450 |
142.670 |
30 сек. |
|
Локально-одномерный метод |
5 |
51 |
51 |
147.941 |
147.190 |
146.630 |
146.142 |
145.692 |
145.263 |
144.848 |
15 сек. |
На рис.1 показано уменьшение давления в скважине N=5. На временном шаге каждого метода показаны разные значения. Но эти значения очень приближены друг к другу. На графике метод переменных направлений и метод покомпонентного расщепления очень близки по значениям. Это указывает на то, что эти методы очень приближены по точности, погрешности и устойчивости. В табл. 1 приведено время счета для решения задачи. Наша задача двухмерная, поэтому для определения оптимального алгоритма мы не будем рассматривать только точность, сходимость и приближенность методов. Время счета тоже играет большую роль.
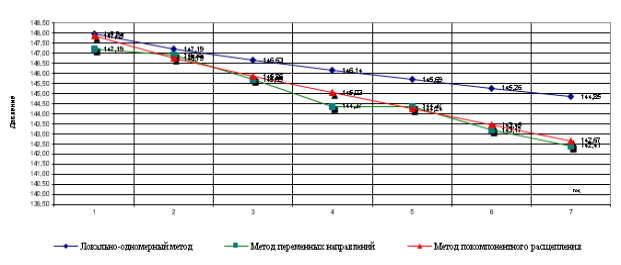
Рис. 1. Полученные результаты по годам в центральной скважине
Поэтому рассмотрев результаты табл. 1, полученные с помощью приведенных методов, мы можем определить оптимальный алгоритм для управления фильтрационными системами. Из таблиц и графика видно, что метод переменных направлений по сходимости, точности, приближенности и времени счета обеспечивает хороший результат для поставленной задачи.
Теперь рассмотрим задачу если даны дебиты в 9 скважинах. Число скважин № =9. А дебиты в каждой добывающей скважине постоянны и равны Q=103 м3/сутки. Остальные все исходящие данные не будем изменять. Требуется определить изменение давления в каждой скважины по времени. Эти скважине расположены симметрично и номера этих скважин NS=9. Фонд скважин в координатной системе приведен в табл. 2.
Решаем задачу, используя все приведенные методы, и получим результаты, данные в табл. 2–4.
Таблица 2
Полученные результаты спомощью локально-одномерного метода (Время счета 15 сек.)
|
|
OX |
OY |
Год разработки |
||||||
|
№скв |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
21 |
21 |
145.6860 |
143.8807 |
142.3330 |
140.8420 |
139.3651 |
137.8912 |
136.4172 |
|
2 |
51 |
21 |
145.5624 |
143.6446 |
141.9983 |
140.4292 |
138.8939 |
137.3778 |
135.8739 |
|
3 |
81 |
21 |
145.6860 |
143.8807 |
142.3330 |
140.8420 |
139.3651 |
137.8912 |
136.4172 |
|
4 |
21 |
51 |
147.3424 |
145.8741 |
144.4629 |
143.0372 |
141.5952 |
140.1417 |
138.6805 |
|
5 |
51 |
51 |
147.2699 |
145.7145 |
144.2156 |
142.7161 |
141.2174 |
139.7225 |
138.2318 |
|
6 |
81 |
51 |
147.3424 |
145.8741 |
144.4629 |
143.0372 |
141.5952 |
140.1417 |
138.6805 |
|
7 |
21 |
81 |
145.6860 |
143.8807 |
142.3330 |
140.8420 |
139.3651 |
137.8912 |
136.4172 |
|
8 |
51 |
81 |
145.5624 |
143.6446 |
141.9983 |
140.4292 |
138.8939 |
137.3778 |
135.8739 |
|
9 |
81 |
81 |
145.6860 |
143.8807 |
142.3330 |
140.8420 |
139.3651 |
137.8912 |
136.4172 |
Таблица 3
Полученные результаты с помощью метода переменных направлений (Время счета 15 сек.)
|
|
OX |
OY |
Год разработки |
||||||
|
№скв |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
21 |
21 |
145.5734 |
144.9712 |
141.9393 |
140.9749 |
138.3799 |
137.2436 |
134.8547 |
|
2 |
51 |
21 |
145.4463 |
144.7815 |
141.6413 |
140.6909 |
138.0574 |
136.9357 |
134.5310 |
|
3 |
81 |
21 |
145.5734 |
144.9712 |
141.9393 |
140.9749 |
138.3799 |
137.2436 |
134.8547 |
|
4 |
21 |
51 |
145.4463 |
144.7815 |
141.6413 |
140.6909 |
138.0574 |
136.9357 |
134.5310 |
|
5 |
51 |
51 |
145.3153 |
144.5705 |
141.3207 |
140.3865 |
137.7138 |
136.6075 |
134.1867 |
|
6 |
81 |
51 |
145.4463 |
144.7815 |
141.6413 |
140.6909 |
138.0574 |
136.9357 |
134.5310 |
|
7 |
21 |
81 |
145.5734 |
144.9712 |
141.9393 |
140.9749 |
138.3799 |
137.2436 |
134.8547 |
|
8 |
51 |
81 |
145.4463 |
144.7815 |
141.6413 |
140.6909 |
138.0574 |
136.9357 |
134.5310 |
|
9 |
81 |
81 |
145.5734 |
144.9712 |
141.9393 |
140.9749 |
138.3799 |
137.2436 |
134.8547 |
Таблица 4
Полученные результаты спомощью метода покомпонентного расщепления (Время счета 30 сек.)
|
|
OX |
OY |
Год разработки |
||||||
|
№скв. |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
21 |
21 |
147.2955 |
145.2404 |
143.2324 |
141.2162 |
139.1946 |
137.1710 |
135.1471 |
|
2 |
51 |
21 |
147.2129 |
145.0577 |
142.9928 |
140.9497 |
138.9170 |
136.8896 |
134.8653 |
|
3 |
81 |
21 |
147.2955 |
145.2582 |
143.2653 |
141.2615 |
139.2502 |
137.2349 |
135.2178 |
|
4 |
21 |
51 |
147.1841 |
145.0335 |
142.9683 |
140.9248 |
138.8921 |
136.8649 |
134.8408 |
|
5 |
51 |
51 |
147.0968 |
144.8392 |
142.7148 |
140.6439 |
138.5998 |
136.5689 |
134.5443 |
|
6 |
81 |
51 |
147.1841 |
145.0524 |
143.0028 |
140.9720 |
138.9495 |
136.9306 |
134.9132 |
|
7 |
21 |
81 |
147.2955 |
145.2554 |
143.2635 |
141.2610 |
139.2507 |
137.2364 |
135.2199 |
|
8 |
51 |
81 |
147.2129 |
145.0735 |
143.0252 |
140.9959 |
138.9744 |
136.9563 |
134.9393 |
|
9 |
81 |
81 |
147.2955 |
145.2725 |
143.2950 |
141.3045 |
139.3041 |
137.2979 |
135.2880 |
Сравнение результатов таблиц показали следующее: по табл. 4 давление уменьшается быстрее, чем по табл. 2–3. Полученные результаты приведены на временном шаге t=360. Для проверки результатов на временном шаге t=7 построим график на основе табл. 1.
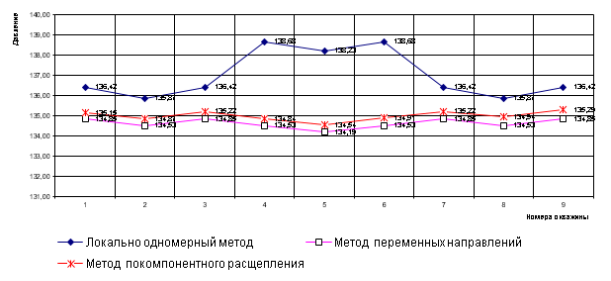
Рис. 2. Полученные результаты в скважинах за конечный год
На рис. 2 по направлению ОУ показано изменение давления, по направлению ОХ — номера скважин. Рассмотрев рис. 2, отметим, что методы переменных направлений и покомпонентного расщепления дают лучший результат, чем локально-одномерная схема. А время счета меньше методе переменных направлений чем, по методу покомпонентного расщепления. Таким образом, для выбранной двухмерной задачи можно применять метод переменных направлений, который дает хорошие результаты по точности, погрешности, устойчивости и по времени счета.
Литература:
- Дементьев Л. Ф. Математические методы и ЭВМ в нефтегазовой геологии. — М.: Недра, 1983. — 189 с.
- Жакбаров О. О., Имамназаров Э. Д., Кодиров З. З. Создание пакета прикладных программ для оптимального управления процессом фильтрации для разработки газовых месторождений // Молодой ученый. — 2015. — № 9. — с. 226–230.







