Annotation. The article is devoted to the problem of formation of logical thinking math class students through interactive support schemes. An example of an interactive support scheme entitled "Methods for solving systems of equations with two variables."
Keywords: interactive support schemes, logical thinking, math lesson.
Реалии современного мира таковы, что человек вынужден оперировать большими объемами информации, как в профессиональной, так и в повседневной жизни. В сложившихся условиях перед школой стоит задача вооружения учащихся инструментами оперативного поиска, отбора, анализа и обработки информации для принятия жизненно важных решений, поиска закономерностей, аналогий, нахождения оптимальных методов решения профессиональных задач. Особое значение в связи с рассматриваемой проблемой приобретает логическое мышление как один из основных видов человеческого мышления. Его роль особенно возрастает в связи с изучением предметов естественнонаучного цикла, где необходимо строить математические модели решаемых задач, уметь четко планировать последовательность действий при выполнении той или иной операции, находить и устранять логические ошибки в алгоритмах действий.
Математизация знаний, их отрыв от наглядности еще больше усиливает значение логического мышления. Как отмечает А.Ф. Лосев, «если мышление функционирует, - математика создается; и, если оно прекращается, прекращается математика. В математике или есть мышление, тогда она - математика; или нет, тогда падает и математика» [3, с. 289].
Теоретические исследования, посвященные анализу понятия мышления, выявлению способов его развития у учащихся содержатся в современной философской и психолого-педагогической литературе. Так, Э.В. Ильенков занимался проблемой диалектики абстрактного и конкретного мышления, выявил их структурные компоненты, уточнил категориальный аппарат понятия мышления в ряду категорий материалистической диалектики. Он считал, что учить человеческому мышлению - значит учить диалектике, и поскольку «мышление есть универсальная (всеобщая) определенность человека, то система образования обязана в каждом индивиде заложить на деле эту всеобщую основу» [1, с. 43].
Виды мышления можно классифицировать по разным основаниям.
1. По генезису развития:
а) наглядно-действенное мышление, опирающееся на непосредственное восприятие предметов в процессе действий с ними;
б) наглядно-образное мышление, характеризующееся опорой на представления и образы;
в) словесно-логическое мышление, осуществляемое в процессе логических операций с понятиями на выявление существенных закономерностей и взаимосвязей исследуемой реальности;
г) абстрактно-логическое мышление, основанное на выделении существенных свойств и связей предмета и отвлечении от других, несущественных.
2. По характеру решаемых задач:
а) теоретическое мышление, основанное на теоретических рассуждениях и умозаключениях;
б) практическое мышление, опирающееся на суждения и умозаключения, основанные на решении практических задач.
3. По степени развернутости:
а) дискурсивное (аналитическое) мышление, характеризующееся логикой рассуждений, а не восприятия;
б) интуитивное мышление, опирающееся на чувственное восприятие и отражение воздействий предметов и явлений объективного мира.
4. По степени новизны и оригинальности:
а) репродуктивное мышление на основе образов и представлений, почерпнутых из каких-то определенных источников;
б) продуктивное мышление на основе творческого воображения.
Любая из этих классификаций подходит для школьного образования.
В связи с изменившимися требованиями ФГОС ООО к подготовке выпускника школы особое значение приобретает вопрос формирования культуры мышления школьника. Естественно, что культура мышления предполагает в своей основе, прежде всего, формирование логического мышления. Этому, в частности, посвящены работы Л.И. Бондаренко, Ю.А. Петрова, В.Н. Брюшинкина и др.
В педагогике и психологии проведено немало исследований, посвященных развитию различных видов мышления учащихся, в том числе и логического (А.В. Брушлинский, Л.Л. Гурова, В.В. Давыдов, Г.И. Железовская, Я.И. Лернер, Н.А. Менчинская, Я.А. Пономарев, И.С. Якиманская и др.).
Операционными компонентами мышления являются мыслительные операции анализа, синтеза, сравнения, обобщения, абстрагирования, конкретизации, классификации и систематизации. Каждая из них является компонентом умственной деятельности человека. Действительно, умственная деятельность, как правило, направлена на распознавание или преобразование тех или иных объектов. Например, для того чтобы провести классификацию объектов, нужно выполнить следующие действия: определить ее цель → выявить признаки классифицируемых объектов → сравнить между собою объекты по общим и особенным признакам в соответствии с поставленной целью → выделить основания для классификации в соответствии с намеченной целью и обнаруженными общими и особенными признаками → разделить объекты на группы → назвать каждую выделенную группу → соотнести результат классификации с поставленной целью.
Известно, что влияние математики на развитие общей культуры мышления школьников очень велико. А потому каждому учителю-предметнику необходимо строить учебно-воспитательный процесс таким образом, чтобы сделать это воздействие наиболее эффективным и заметным, создать благоприятные условия для развития всех учащихся (не зависимо от уровня их предметной подготовки).
Анализ основной образовательной программы по математике [5] показывает, что развитие мышления учащихся (в том числе, логического мышления) является одной из основных задач изучения предмета.
Проблеме формирования мыслительных действий посвящены работы многих педагогов и психологов (А.Г. Шашков, А.В. Степанов, П.Я. Гальперин, В.В. Сериков и др.). Структура мыслительных операций неоднократно использовалась исследователями и учителями-предметниками для работы с обобщающими таблицами, блочной подачей материала, опорными схемами (например, метод опорных схем В.Ф. Шаталова, который интересен нам с разных позиций). Модернизация метода опорных схем на основе ИКТ-технологий могла бы открыть в нем огромные потенциальные возможности для развития логического мышления учащихся.
Итак, вопрос использования интерактивных опорных схем на уроках математики имеет большое практическое значение для современной школы. К сожалению, в практике работы общеобразовательных школ развитие логического мышления учащихся на основе их использования не имеет широкого распространения, во-первых, потому что не всегда методологическая и психолого-педагогическая подготовка учителя находится на должном уровне; во-вторых, потому что недостаточно необходимых теоретических разработок; в-третьих, потому что педагогический опыт по исследуемой проблеме пока еще не подкреплен экспериментальными данными; в-четвертых, потому что отсутствуют специальные подборки интерактивных опорных схем.
Мы полагаем, что развитие логического мышления старшеклассников может быть эффективным при следующих условиях:
1) если в основу модели развития логического мышления учащихся будет положена система личностно ориентированных учебных ситуаций, направленных на формирование логического мышления через использование интерактивных опорных схем;
2) если учитель будет знать принципы построения системы интерактивных опорных схем по каждой теме изучаемого материала.
Рассмотрим отличительные особенности использования метода интерактивных опорных схем на уроках математики.
Подача материала большими блоками способствует целостному и осознанному восприятию материала, делает понятным для учащихся введение и изучение многих математических фактов, понятий, их свойств, правил, теорем и т.п., а также раскрывает их внутреннюю взаимосвязь друг с другом. При изучении темы ученик на уроке и дома (используя возможности передачи информации по глобальной сети) видит перед собой интерактивные опорные плакаты и схемы; не раз, готовясь к письменному ответу, выполняя домашнее задание или сдавая теоретический зачет, он самостоятельно выполняет ту или иную часть такой схемы. Многократно он слышит изложение материала учителем и своими одноклассниками, а также проговаривает его сам. Такая организация учебного процесса способствует, с одной стороны, развитию всех видов памяти ученика; с другой стороны, более быстрому и качественному запоминанию и пониманию каждой конкретной темы.
Кроме того, использование интерактивных опорных схем способствует формированию ИКТ-компетентности учащихся, поддерживает интерактивный режим работы на уроке и дома, сокращает время подготовки к ответу, тем самым способствуя решению проблемы загруженности ребят [2, 4].
В качестве примера приводим фрагмент урока алгебры 9 класса на тему «Методы решения систем уравнений с двумя переменными».
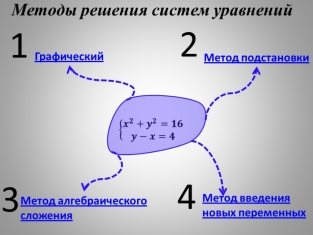
В школьном курсе математики уравнения с двумя переменными решают четырьмя основными методами: графический, подстановки, алгебраического сложения и введения новой переменной. На уроке обобщения и систематизации по данной теме целесообразно прибегнуть к использованию интерактивных опорных схем, первая из которых приведена на рис. 1.
|
Рис. 1. Интерактивная опорная схема «Методы решения систем уравнений» |
Рис. 2. Интерактивная опорная схема «Графический метод решения систем уравнений» |
Переходы между слайдами с использованием гиперссылок позволяют последовательно повторить весь теоретический материал по теме.
Первой частью интерактивной схемы станет «Графический метод решения систем уравнений». Рассмотрим систему уравнений с двумя переменными
.
Решение. Построим график уравнения х2+у2=16 -окружность с центром в начале координат и радиусом 4. Построим график уравнения у‑х=4. Это прямая, проходящая через точки (0; 4) и (-4; 0). Окружность и прямая пересекаются в точках А и В. Судя по построенной геометрической модели, точка А имеет координаты (-4; 0), а точкаВ‑ координаты (0; 4). Проверка показывает, что на самом деле пары (-4; 0) и (0; 4) являются решениями обоих уравнений системы, а значит, и решениями системы уравнений. Следовательно, заданная система уравнений имеет два решения: (-4; 0) и (0; 4).Ответ: (-4; 0); (0; 4) (рис. 2).
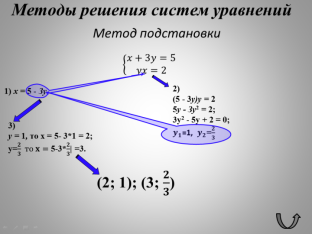
Рассмотрим метод подстановки на примере системы 
.
Этот метод применялся учащимися в 7-м классе для решения систем линейных уравнений. Алгоритм, который был отработан в 7-м классе, пригоден для решения систем любых двух уравнений с двумя переменными. Он заключался в последовательном выполнении следующих действий: а) выразить у через х из одного уравнения системы; б) подставить полученное выражение вместо у в другое уравнение системы; в) решить полученное уравнение относительно х; г) подставить каждый из найденных на третьем шаге корней уравнения поочередно вместо х в выражение у через х, полученное на первом шаге; д) записать ответ в виде пар значений (х;у), которые были найдены соответственно на третьем и четвертом шаге.
Переменные х и у равноправны, поэтому на первом шаге алгоритма можно выразить не у через х, а х через у. Обычно выбирают то уравнение, которое представляется более простым, и выражают ту переменную из него, для которой эта процедура представляется более простой (рис. 3).
|
Рис. 3. Интерактивная опорная схема «Метод подстановки для решения систем уравнений» |
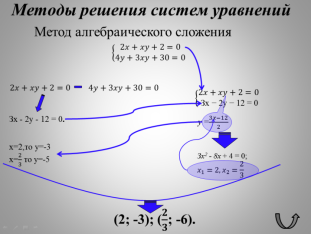
Рис. 4. Интерактивная опорная схема «Метод алгебраического сложения для решения систем уравнений» |
Решение. Выразим х через у из первого уравнения системы: х=5‑3у.Подставим полученное выражение вместо х во второе уравнение системы: (5‑3у)у=2. Решим полученное уравнение:5у‑3у2=2;3у2‑6у+2=0; 
=1, 
=
. Подставим поочередно каждое из найденных значений у: если у=1, то х=5‑3·1=2; если y=
5‑3·=3.Пары (2; 1) и (3; )‑ решения заданной системы уравнений. Ответ: (2; 1); (3;).
Рассмотрим метод алгебраического сложения для системы уравнений 
. Этот метод также знаком учащимся из курса алгебры 7-го класса, где он применялся для решения систем линейных уравнений.
Решение. Умножим все члены первого уравнения системы на 3, а второе уравнение оставим без изменения:
.Вычтем второе уравнение системы из первого: (6х+3ху+6)‑(4у+3ху+30)=0‑0;6х‑4у‑24=0;3х‑2у‑12=0.В результате алгебраического сложения двух уравнений исходной системы получилось новое более простое уравнение. Этим уравнением заменим любое из уравнений первоначальной системы, например, второе. Тогда система уравнений примет вид:
.Эту систему можно решить методом подстановки. Из второго уравнения находим:
. Подставив это выражение вместо у в первое уравнение системы, получим:3х2‑8х+4=0; х1=2; х2=. Осталось подставить найденные значения х в формулу 3х‑2у‑12=0. Если х=2, то у=‑3. Если х=, то у=‑5. Ответ: (2; ‑3), (; ‑6) (рис. 4).
Метод введения новой переменной удобно проиллюстрировать на примере системы уравнений, одно из которых – дробно-рациональное (рис. 5).
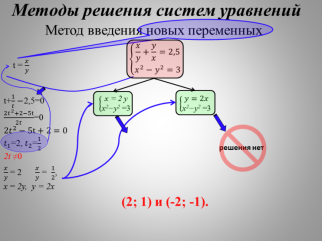
Рис. 5. Интерактивная опорная схема «Метод введения новой переменной для решения систем уравнений»
Решим систему уравнений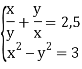
.
Решение. Введем новую переменную
. Тогда первое уравнение системы можно будет переписать в более простом виде: с+
‑2,5=0. Решим это уравнение относительно переменной с:
; 2с2‑5с+2=0; с1=2; с2=
. Оба этих значения удовлетворяют условию2с≠0, а потому являются корнями рассматриваемого уравнения с переменной с.Но с=
, значит, либо =2, тогда х=2у; либо =, тогда у=2х. Итак, с помощью метода введения новой переменной удалось разбить первое уравнение системы на два более простых:х=2у; у=2х. Теперь каждое из уравнений нужно поочередно рассмотреть в системе с уравнением х2‑у2=3. Т.е., задача сводится к решению двух систем уравнений:
и 
.
Решая первую систему уравнений методом подстановки, получим два решения: (2; 1) и (‑2;‑1).Решая вторую систему уравнений тем же методом, убедимся, что она не имеет решений. Ответ:(2; 1), (‑2;‑1).
Рассмотренная интерактивная опорная схема поможет еще раз кратко повторить все методы решения систем уравнений. На последующих уроках проверка знаний с использованием той или иной части схемы не составит труда. Следует также отметить, что, работая с интерактивной опорной схемой, школьники приучаются логически мыслить, рассуждать, четко формулировать свои идеи и математически грамотно их излагать. Практика показывает, что речь многих учащихся, в начале обучения прерывистая, сбивчивая, постепенно становится последовательной, логически связной и наполненной смыслом.
Изучение материала большими блоками, включающими несколько тем, позволяет разнообразить практические занятия, включая многоплановые задания, для решения которых необходимо знание одновременно нескольких тем, требующих большего напряжения мысли и владения многими навыками.
В качестве критериев развития мышления нами использовались соответствующие показатели, свидетельствующие о достижении учащимся того или иного уровня: а) степень осознанности операций и приемов мыслительной деятельности; б) степень овладения операциями, умениями и приемами мыслительной деятельности, умение производить рациональные действия по применению их в познавательных процессах; в) степень умения осуществлять перенос мыслительных операций и приемов мышления, а также навыков пользований ими на другие ситуации и предметы; г) умение осуществлять перенос знаний из привычной ситуации в нестандартную; степень форсированности различных видов мышления (в том числе логического); д) запас знаний, их системность, а также появление новых способов усвоения знаний; е) степень умения творчески решать задачи, ориентироваться в новых условиях, действовать оперативно; ж) способность усваивать логические суждения и использовать их в учебной деятельности.
Итак, нами была предпринята попытка выявления новой качественной характеристики модели развития логического мышления старшеклассников, которая заключается в создании комплекса интерактивных опорных схем, требующих от учеников сознательного принятия основных законов логического мышления.
Как показала практика, метод интерактивных опорных схем значительно сокращает время, затрачиваемое на выдачу и проверку теоретического материала, а также он является чрезвычайно наглядным, что позволяет ученикам активно использовать зрительную и логическую память.
Метод, предложенный В.Ф. Шаталовым, прошел многолетнюю апробацию, он был открыт в те годы, когда компьютерные технологии были слабо развиты и не распространены. Сегодня, опираясь на метод В.Ф. Шаталова, усовершенствовав его, введя элемент интерактивности, можно получить высокий результат развития мышления школьников. Необходимо сказать, что метод интерактивных опорных схем был апробирован нами на базе МАОУ «Маслянская СОШ» Тюменской области и дал хорошие результаты. Уровень развития логического мышления школьников повысился в среднем на 12%.
В последние годы создание и применение интерактивных схем на уроках математики становится все более актуальным. Ввиду ускоряющихся темпов развития интерактивных технологий в школе, сегодня требуется применение инновационных методов преподавания и интерактивные опорные схемы в этом плане идеально вписываются в современный ритм.
Литература:
- Ильенков, Э.В. Диалектика абстрактного и конкретного в научно-теоретическом мышлении / Э.В. Ильенков. – М.: Ин-т филос. АН СССР, 1960. – 390 с.
- Лапина, Е.А. Формирование ключевых компетенций на уроках математики / Е.А. Лапина, Т.С. Мамонтова // Научные итоги 2011 года: достижения, проекты, гипотезы: сб.материалов I Международ. науч.-практич. конф./ под ред. С.С. Чернова. – Новосибирск, 2011. – Ч. 1. – С. 132-136.
- Лосев, А.Ф. Хаос и структура / А.Ф. Лосев; под ред. А.А. Тахо-Годи, В.П. Троицкого. - М.: Мысль,1997. – 831 с.
- Мамонтова, Т.С. Роль лаборатории интерактивных средств обучения в подготовке будущих учителей математики //XXV Ершовские чтения: сб. науч. ст. / отв. ред. Л.В. Ведерникова. – Ишим, 2015. – С. 93-96.
- Примерная основная образовательная программа образовательного учреждения. Основная школа / [сост. Е. С. Савинов]. – М.: Просвещение, 2011. – 454 с.
