В работе [1] исследуется конструкция центробежно-ударной дробилки. Схема дробилки представлена на рисунке 1.
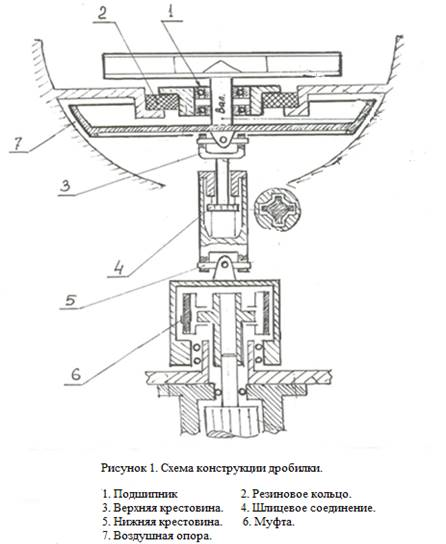
В конструкции дробилки выделяются элементы подвижной части: центробежная муфта подсоединения силового электродвигателя вращения; карданный вал из двух частей (нижней и верхней) со шлицевым соединением, обеспечивающим удлинение или укорочение вала; ротор в виде совокупности воздушной опоры и ускорителя дробимой породы, соединенных валом; втулка подшипникового узла вала с опертым на корпус дробилки резиновым кольцом.
Каждое из выделенных устройств – муфта, низ карданного вала, верх карданного вала, ротор, втулка – моделируется абсолютно жестким телом. Пять тел объединяются в систему упруго-вязкими связями.
На основе классических положений теоретической механики [3] движение подвижной части дробилки описывается системой восемнадцати обыкновенных дифференциальных уравнений.
Для исследования силового воздействия породы конструктивные элементы дробилки моделируются одним твердым телом, которое называется «Ротором». На верхнюю часть Ротора – ускоритель падает дробимая порода в виде более или менее однородных кусков. Ускоритель дробилки в виде плоского диска с перегородками, подвешен на воздушной опоре и центрируется шарикоподшипниковой опорой. Диск вращается вокруг оси вала с заданной угловой скоростью Ω, сохраняя горизонтальное положение.
При попадании в дробилку, камень движется вдоль направляющих ускорителя по радиусу от центра наружу см. Рис 2.
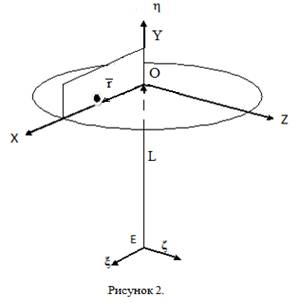
Требуется составить выражения для составляющих силы F и момента 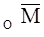 , как функций времени от момента соприкосновения камня с ускорителем дробилки.
, как функций времени от момента соприкосновения камня с ускорителем дробилки.
Движение камня по ускорителю в инерциальной системе отсчёта 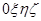 описывается уравнением
описывается уравнением
mk 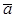
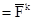
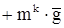 .
.
При этом введено допущение: движущийся камень действует на ускоритель тремя силами, приложенными в точке текущего положения камня на ускорителе. Силы таковы: вдоль оси вала сверху вниз от веса камня – mg, вдоль перегородки от центра диска - 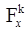 ; перпендикулярно перегородке в сторону перегородки -
; перпендикулярно перегородке в сторону перегородки - 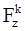 .
.
Выполним абсолютное дифференцирование [2]:
Первая производная: 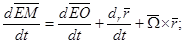
Вторая производная: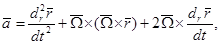
В проекциях на оси OX, OY, OZ получим дифференциальные уравнения:
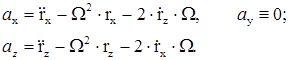
Уравнения движения камня: 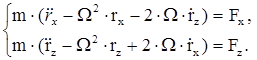 .
.
Т.к. 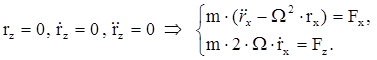 , решая верхнее уравнение, как линейное неоднородное второго порядка, получаем:
, решая верхнее уравнение, как линейное неоднородное второго порядка, получаем:
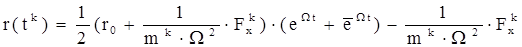
В нашем случае:
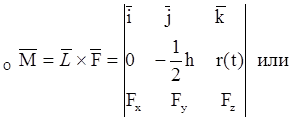
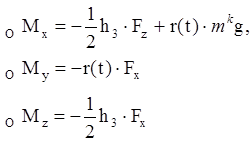
Расчётные формулы для сил:
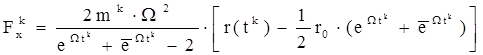
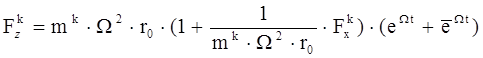
Исходные данные: 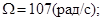
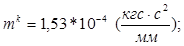
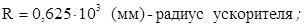
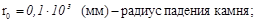
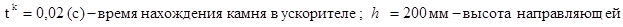
Используя конкретные значения масс, скорости и размеров реальной дробилки получим численные оценки сил и моментов на ускоритель:
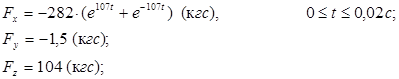
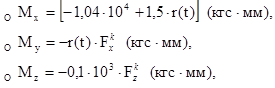 где
где 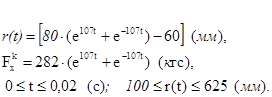
Таким образом, в правые части векторных уравнений движения «Ротора» подставляются выражения:
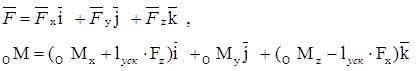
В ранее проводимых расчетах, воздействия породы на ротор, предполагалось, что моменты и силы постоянные. Не учитывалось движение массы по ускорителю. В данном случае, по полученным формулам, можно вычислять переменные моменты и силы, которые воздействуют на ротор. Зная силовое воздействие дробимой породы на ротор можно более точно прогнозировать работоспособность дробилки.
ЛИТЕРАТУРА
1. Сентяков В.А. Математическая модель центробежного роторного оборудования ударно-отражательного типа. Журнал из списка рекомендованных ВАК: «Научно-технические ведомости СПбГПУ. Раздел: Математическое моделирование: методы, алгоритмы, технологии. Издательство Политехнического университета №6(69)2008. – C.175-179.
2. И.Я.Огурцов. Дифференциальные уравнения движения трехосного гироскопического стабилизатора на движущемся основании. Общие положения. СерияХ, №110.ОНТИ-609,1980. УДК 629.7.054’847:231.4.
3. Лойценский Л.Г., Лурье А.И. Курс теоретической механики: В 2 т. – М.: Наука, 1984.







