Целью работы является определение символьных решений термоупругой задачи устойчивости труб обсадных колонн, находящихся в многолетнемерзлых горных породах. Проблема устойчивости составляющих конструкцию нефтяных и газовых скважин, обсадных колонн в многолетнемерзлых породах вследствие разности температурных градиентов во внутриколонном и горных пород в заколонном пространствах изучена в деталях.
Строительство и эксплуатация нефтяных и газовых скважин в вечномерзлых грунтах нередко сопровождаются осложнениями, связанными с растеплением и обратным промерзанием пород, слагающих околоскважинное пространство. В результате, в окрестности скважины возникают внешние сминающие горные давления, приводящие к нарушению ее крепи, в частности, смятию обсадных колонн, спущенных в многолетнемерзлых породах (ММП).
Вопросу устойчивости составляющих конструкцию нефтяных и газовых скважин обсадных колонн в многолетнемерзлых породах в результате разности температурных градиентов жидкости внутри обсадной колонны и горных пород в заколонном пространстве посвящено много работ [1-9]. Однако ряд вопросов, касающихся влияния параметров несовершенств формы труб и физико-механических свойств мерзлых горных пород на устойчивость колонн, требуют решения.
Целью работы является совершенствование метода решения термоупругой задачи устойчивости несовершенных по форме обсадных колонн в многолетнемерзлых породах с помощью символьной алгебры системы Mathematica. Компьютерные методы моделирования поставленной задачи основываются на встроенных в Mathematica прикладных пакетах.
В основу совершенствованной методики расчета критических давлений на составляющих конструкцию нефтегазовых скважин обсадные трубы положена теория термоупругости тонкостенных цилиндрических оболочек, стесненных упругими горными породами.
Как известно, жидкость в колонне при бурении скважины так же, как и добываемый флюид при ее эксплуатации, имеют температуру выше, чем у горных пород в околоствольном пространстве, поэтому температурные напряжения, возникающие в стенке обсадной колонны, являются составляющими напряженного состояния трубы вследствие всестороннего сжатия обсадной колонны горным давлением.
Для решения поставленной выше задачи рассмотрим стационарное распределение температур в заколонном пространстве вертикальной скважины. Предполагается, что распределение температуры вокруг обсадной колонны не зависит от мощности расположенной в окрестности нее горной среды (слоя). Составим в компьютерной среде Mathematica совместную краевую задачу для трубы обсадной колонны и горной породы и найдем соответствующие символьные решения системы уравнений равновесия обсадной трубы, включая распределение температуры вокруг скважины.
Методика решения названных краевых задач с использованием символьной алгебры системы Mathematica представлена ниже
Для обсадной колонны и горной породы составлены:
- уравнения стационарного распределения температур:
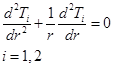, (1)
где индекс 1 относится к обсадной колонне, а 2 – к горной породе в окрестности скважины;
- граничные условия для уравнения стационарного распределения температур:
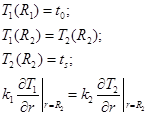(2)
- уравнения Лямэ для смещений трубы и горной породы:
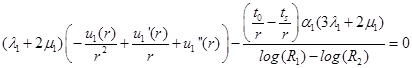(3)
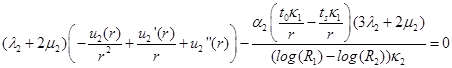(4)
- граничные условия для уравнения Лямэ:
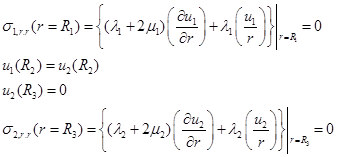(5)
В формулах введены следующие обозначения:
· 
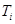- температуры фаз;
· 
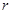-текущая радиальная координата границы раздела фаз;
· 
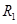- внутренний радиус колонны (скважины);
· 
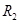- радиус наружной поверхности трубы – расстояние, на котором устанавливается температура пород;
· 
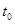- температура на внутренней стенке трубы;
· 
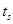- температура на наружной поверхности трубы;
· 
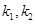- коэффициенты теплопроводности трубы и породы;
· 
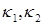- коэффициент температуропроводности трубы и породы;
· 
,
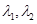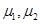- постоянные Лямэ;
· 
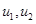- радиальные смещения в трубе и горной породе;
· 
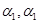- коэффициент линейного температурного расширения трубы и породы;
· 
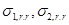- радиальные напряжения в стенке трубы и горной матрице;
· 
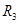- радиус зоны протаивания окружающих скважину мерзлых пород.
Пример символьного решения для распределения температур вокруг скважины приведен ниже.
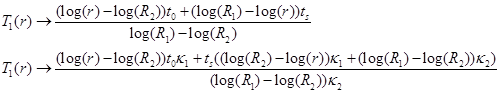(6)
В результате символьного решения системы (3-5) получены конечные формулы напряжений и деформации соответственно для трубы и горной породы. Полученная с применением компьютерной алгебры в среде Mathematica формула смещения в трубе и горной породе имеет вид:
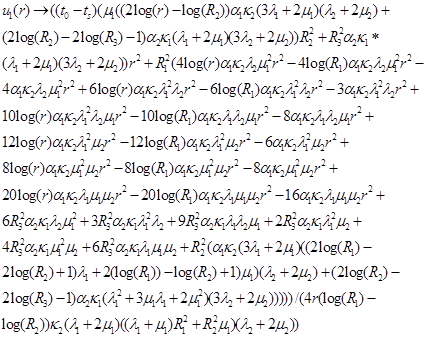(7)
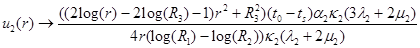(8)
Полученные решения (7) и (8) позволяют получить все составляющие тензоров напряжений и деформаций в обсадной трубе и в ММП.
Известно, что при строительстве нефтяных и газовых скважин в толще многолетнемерзлых пород обычно спускаются и крепятся составляющие их конструкцию направление и кондуктор. Поэтому в данной работе рассматривается термоупругая задача устойчивости наиболее подверженной смятию обсадной колонны, кондуктора, диаметром 244,5×10 мм на примере скважины Песчаноозерского месторождения, расположенного на острове Колгуев Ямало-Ненецкого административного округа.
На рисунках 1 представлены совмещенные графики соответственно радиальных и кольцевых напряжений в трубе обсадной колонны (кондуктора) 244,5 мм с толщиной стенки 10 мм, при изменении температуры в ней от + 10 °С до – 1,98 °С и в горном скелете при температуре окружающей скважину породы, равной – 1,98 °С.
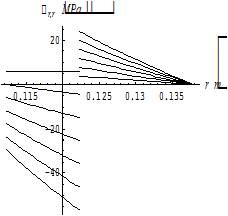
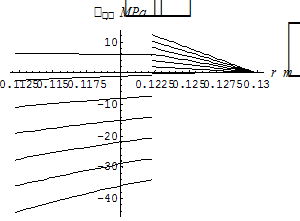
а б
Рис. 1. Совмещенный график напряжений в обсадной трубе (кондуктора) диаметром 244,5 мм с толщиной стенки 10 мм и в горном скелете: а – радиальные напряжения; б – кольцевые напряжения..
Очевидно (рис. 1), что радиальные напряжения максимальны на внутренней поверхности стенки трубы кондуктора и изменяются от сжимающих до растягивающих, а окружные напряжения являются знакопеременными, которые при изменении температуры приводят к потере устойчивости обсадной трубы.
Окружные напряжения в горной породе являются растягивающими, т.е. разрывными по своей физической сути, приводящими к разрушению горных пород в за пространсиве.
Таким образом, полученные решения для напряженно-деформированного состояния в обсадной трубе и в горном скелете вследствие разности температурных градиентов жидкости внутри обсадной колонны и пород в заколонном пространстве приводят как к разрушению горных пород в окрестности скважины, так и к потере несущей способности кондуктора одновременно.
: Разработаны оригинальные, ранее не применявшиеся, подходы и способы решения термоупругой задачи устойчивости несовершенных по форме обсадных колонн в многолетнемерзлых породах методами символьной алгебры системы Mathematica, которы можно применять при проектировании конструкций морских нефтяных и газовых скважин в акватории Арктических морей России
Список литературы:
- Антипов В.И., Нагаев В.Б., Седых А.Д. Физические процессы нефтегазового производства: Учеб. пособие для вузов. В 3-х т. – М.: ОАО «Издательство «Недра», 1988. Т.1. – 372 с.
- Булатов А.И. Макаренко П.П., Будников Ю.М. Теория и практика заканчивания скважин: В 5 т. – М.: ОАО «Издательство «Недра», 1988. – Т. 4. – 496 с.
- Кудряшов Б.Б., Яковлев А.М. Бурение скважин в мерзлых породах. М., Недра, 1983. – 286 с.
- Тимошенко, С.П. Курс теории упругости / С.П. Тимошенко. – Киев: "Наукова думка", 1972. – 501 с.
- Carman A.P. Resistnce of tube to collapse. Bulletin of Illinois University, 1906, vol.3, № 17, pp.1-26.
- Stewart R.T. Collapsing pressre of bessemer steel lapwelled tubes, three to ten inches in diameter. Transections of the American Society of Mechanical Engineers, 1906, vol.27, № 1115, pp.730-821.
- Медведский Р.И. Строительство и эксплуатация скважин на нефть и газ в вечномерзлых породах. – М.: Недра, 1987, - 230 с., ил.
- Ползков А.В. Особенности расчета давлений гидроразрыва многолетнемерзлых пород и аномальных давлений, воздействующих на крепь скважин при обратном промерзании / НТЖ. Строительство нефтяных и газовых скважин на суше и на море. – М.: ОАО «ВНИИОЭНГ», 2000 – № 4. – С. 14 – 22.
- Леонов Е.Г., Зайцев О.Ю. Расчет содержания фаз и давления при замерзании водосодержащих сред в заколонном и межколонном пространствах скважин промерзании / НТЖ. Строительство нефтяных и газовых скважин на суше и на море. – М.: ОАО «ВНИИОЭНГ», 2005 – № 1. – С. 10 – 16.
- Дьяконов, В. Mathematica 4: учебный курс / В. Дьяконов. – С-Пб.: Питер, 2001. – 656 с.
