Суммарное тяговое сопротивление бокового рабочего органа складывается из сопротивления почвы перемещению долота (Rд), стойки (Rc), и рыхлительной пластины (Rп), т. е.
Rб =Rд +Rc +Rп (1)
Тягового сопротивления долота (Rд):
Rд = K1 ƿ tl bl+£h(bd+hctg ψ2) {cos ψn + fsin(α+ψn)COSα}/sin ψn +{(hctg ψ2 +hctgψ2)hγ + (2 hctg ψ2 + bd +HtgѲ γ1}V2sinαtg(α+γ) + bd(hγ+Hγ1) hdgtg(α+γ)/sinα (2)
Стойка рабочего органа взаимодействует с разрушенной долотом почвой и раздвигает ее в стороны. Силу сопротивления ее определяем, пользуясь схемой, приведенной на рис 1.
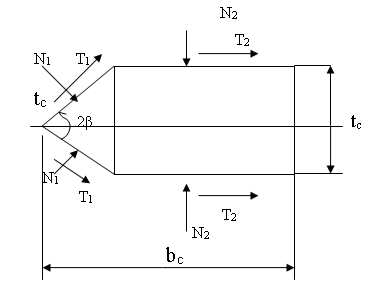
Рис. 1. Схема сил, действующих на стойку
Rc=2N1sinβ+2T1cosβ + 2T2(3)
где N1- сила нормального давления почвы на переднюю грань стойки;
Т1= fN1- сила трения, возникающая на передней грани стойки;
T2=fN2- сила трения, возникающая на боковой грани стойки;
Rc = 2N1sinβ+2fN1cosβ + 2fN2(4)
Выразим N1 ии N2 через удельное давление почвы на переднюю грань стойки и ее геометрические размеры
Rc=qntc(h+H)(1+ftgβ+fqб(h+H)(2bc — tcctgβ) (5)
Где qn — удельное давление почвы на переднюю грань стойки;
qб- удельное давление почвы на боковую грань стойки;
bc — ширина стойки;
tc — толщина стойки;
β — половина угла заострения стойки.
Выведем зависимость для определения сопротивления почвы перемещению рыхлительной пластины. В процессе работы рыхлительная пластина преодолевает сопротивление R2 1 почвы деформации и силу трения, возникающую от этой силы на рабочей поверхности рыхлительной пластины, сопротивление R31, обусловленное силой инерции почвы и сопротивление R41 уу перемещению в сторону, т. е.
Rп = R2 1+ R31+R41 (6).
Сопротивление почвы деформации можно определить, спроектировав силу S1 сопротивления почвы сдвигу и силу трения, возникающую от этой силы на рабочей поверхности рыхлительной пластины, по направлению движения.
R2 1= S1 sin(γn+φ) + f S1cosφcosγn= S1{sin(γn+φ)+sinφcosγn} (7)
Сила сопротивления сдвигу равна
S1=τ(2a-bn)bncosφ/2cos(γn+φ) sin γn (8)
Аналогичным образом определяем сопротивление почвы перемещению в сторону
Т1=Т1{sin(γn+φ)+sinφcosγn} (9)
Где Т1- сила трения почвы, перемещаемой рыхлительной пластиной.
Силу трения Т1 определяем путем умножения силы тяжести перемещаемой рыхлительной пластиной почвы
На коэффициент ее внутренного трения, т. е.
Т1=f1G(10)
Где f1- коэффициент внутренного трения почвы,
G=Fавсдhnγg=(2a-bn)bncosφ/2cos(γn+φ) sin γn ‘hnγg(11)
Подставив значение G в 10, а затем Т1 в 9, окончательно записиваем
R41= f1(2a-bn)bncosφ/2cos(γn+φ) sin γn ‘hnγg{ sin(γn+φ)+sinφcosγn }(12)
Уравнение, выражающее закон изменения количества движения перемещаемой рыхлительной пластиной почвы по направлению, перпендикулярному к ее рабочей поверхности, имеет следующий вид
Nдdt=dm(Vn-Vno) (13)
Где Nд — динамическая нормальная сила, возникающая на рабочей поверхности рыхлительной пластины;
t –время;
Vn- проекция абсолютной скорости перемещения частиц почвы на нормаль рабочей поверхности рыхлительной пластины;
Vno- начальная скорость перемещения частиц почвы;
m- масса почвы, перемещаемая рыхлительной пластиной.
Nд=dm/dtVn(14)
Масса почвы, перемешаемая рыхлительной пластиной в единицу времени, равна
dm/dt= ahnVγ(15)
Подставив значение 15 в 14 и учтя, что Vn= Vsinγn, получаем
Nд= ahnV2γsin γn(16)
Таким образом, динамическое давление почвы на рабочую поверхность рыхлительной пластины пропорционально квадрату скорости движения, междуследую рабочих органов. Оно возрастает с увеличением угла установки рыхлительной пластины к направлению движения.
Сила сопротивления перемещению рыхлительной пластины от динамического давления почвы с учетом силы трения, возникающей от нее, равна
R31= Nдsin(γn+φ)/ cosφ = ahnV2γsin γnsin(γn+φ)/ cosφ(17)
Из анализа этого выражения следует, что сила сопротивления, обусловленная инерцией перемещаемой рыхлительной пластиной почвы, с увеличением угла γnи скорости движения возрастает. Подставив значение R2 1, R31 и R41 в (1) записываем
Rп= [(τ+f1hnγg) (2a-bn)bncosφ/2cos(γn+φ) sin γn ‘{ sin(γn+φ)+sinφcosγn }+
+ ahnV2γsin γnsin(γn+φ)/ cosφ(18)
Литература:
- Синеоков Г.Н, Панов И. М., Теория и расчет почвообрабатывающих машин. М.: Машиностроение. 1977. 328с.







