Математическое моделирование социальных процессов, решение задач оптимального управления и планирования приобретают всё большую актуальность в настоящее время в самых разнообразных сферах человеческой деятельности ([1], [2], [3]). К таким моделям можно отнести задачу управления процессом обучения, предложенную в работе [3], где, в том числе, приводится её аналитическое решение. Однако при малейшей модификации модели решение её лишь с помощью аналитического аппарата может стать затруднительным. В статье [4] показано, как данная задача может сформулирована в виде задачи оптимального управления, а также нелинейного программирования, для решения которых разработан ряд эффективных вычислительных алгоритмов ([1]). Целью данной работы является описание и исследование алгоритма численного решения задачи управления обучением студенческого коллектива, формализуемой как задача оптимального управления.
Исследуется задача распределения времени между овладением знаниями и развитием умений. Пусть знание состоит из информации (чистого знания) и умения (практического навыка использовать имеющиеся знания для решения новых задач). Полагаем ![]() – объем сведений, которыми овладел студент к моменту времени t (чистое знание),
– объем сведений, которыми овладел студент к моменту времени t (чистое знание), ![]() — объем отработанных умений решать задачи;
— объем отработанных умений решать задачи; ![]() – та часть (доля) времени, которую педагог отводит на накопление у студентов знаний в промежутке времени
– та часть (доля) времени, которую педагог отводит на накопление у студентов знаний в промежутке времени ![]() . Увеличение
. Увеличение ![]() вычисляется по формуле:
вычисляется по формуле:
![]() ,(1)
,(1)
где k1 > 0 — коэффициент, характеризующий индивидуальные способности учащегося.
Увеличение практических навыков определяется уравнением:
![]() ,(2)
,(2)
где ![]() > 0 — коэффициент, аналогичный k1.
> 0 — коэффициент, аналогичный k1.
Требуется найти управление ![]() из [0;1], которое позволит получить студенту максимальный объем знаний за заданное время T. Заменяя:
из [0;1], которое позволит получить студенту максимальный объем знаний за заданное время T. Заменяя: ![]() ,
, ![]() , получаем задачу оптимального управления:
, получаем задачу оптимального управления:
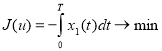 ,(3)
,(3)
![]() ,
, ![]() ,(5)
,(5)
![]() ,
, ![]() .(6)
.(6)
Дискретная задача, аппроксимирующая (3)-(6) с точностью ![]() , имеет вид:
, имеет вид:
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]()
![]() .(7)
.(7)
Введем функцию
![]()
В работе [4] показано, что сопряженные переменные ![]() могут быть вычислены по формулам:
могут быть вычислены по формулам:
![]() ,
,
Алгоритм метода проекции градиента для решения задачи (7)
-
Задаем начальное приближение управления
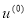 ,
, 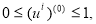
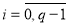 ;
;
-
Вычисляем
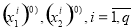 :
: 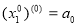 ,
, 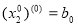 ,
,
![]() ,
, ![]() ;
;
-
Находим
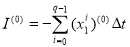 ;
;
-
Определяем
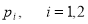 :
: 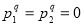 ;
;
![]() ,
,![]()
![]()
- Вычисляем производную функции L по управлению:
![]() ;
;
-
Задаем начальное значение шага
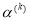 и организуем цикл по шагам градиентного спуска;
и организуем цикл по шагам градиентного спуска;
-
Находим управление
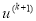 , соответствующее (k+1)-ой итерации, по формуле:
, соответствующее (k+1)-ой итерации, по формуле:
![]() .
.
Для новых значений ![]() управления проверяем условия выполнения ограничений
управления проверяем условия выполнения ограничений ![]() ,
, ![]() . Если условие для некоторого узла i не выполняется, то проецируем управление на допустимое множество.
. Если условие для некоторого узла i не выполняется, то проецируем управление на допустимое множество.
-
Вычисляем соответствующие этому управлению траектории
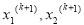 :
:
![]() ,
,![]() ,
, ![]() ,
, ![]() ;
;
- Вычисляем очередное приближение целевой функции:
![]() ;
;
-
Проверяем условие монотонности в методе градиентного спуска. Если
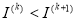 , то уменьшаем шаг градиентного спуска
, то уменьшаем шаг градиентного спуска 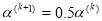 и переходим к шагу 7, иначе полагаем
и переходим к шагу 7, иначе полагаем 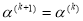 и переходим к шагу 11.
и переходим к шагу 11.
-
Итерационный процесс продолжаем до тех пор, пока не становится достигнутой заданная точность вычислений. Если
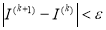 , то идем к шагу 12, иначе полагаем
, то идем к шагу 12, иначе полагаем 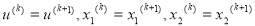
 и повторяем вычисления, начиная с шага 7 алгоритма. Здесь
и повторяем вычисления, начиная с шага 7 алгоритма. Здесь 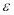 - необходимая точность вычисления функционала.
- необходимая точность вычисления функционала.
-
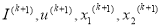 - решение задачи.
- решение задачи.
Данный алгоритм реализован в среде Borland Delphi, при этом решение задачи построено при выборе параметров: ![]() , q=1000, T=1. Результаты численных расчетов приведены на рис.1–3, оптимальное значение функционала
, q=1000, T=1. Результаты численных расчетов приведены на рис.1–3, оптимальное значение функционала ![]() , количество итераций метода
, количество итераций метода ![]() .
.
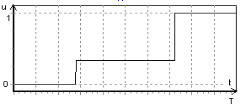
Рис. 1. График
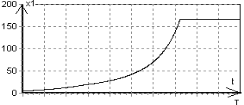
Рис. 2. График ![]()
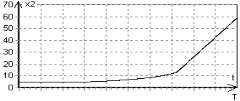
Рис. 3. График ![]()
Результаты численного решения соответствуют следующей организации учебного процесса: на первом этапе нарабатываются практические навыки, опираясь на пройденный материал; далее отношение лекций к практическим занятиям следующее: одной лекции соответствует два семинара; и, наконец, на заключительном этапе проводятся лекции без проработки на практических занятиях. Численное решение задачи совпадает с аналитическим, полученным в [3]. Заметим, что приведенный алгоритм с применением средств ЭВМ открывает широкие возможности для исследования различных модификаций рассматриваемой модели.
Литература:
- Евтушенко Ю. Г. Методы решения экстремальных задач и их применение в системах оптимизации. М.: Наука, 1982.
- Неуймин Я. Г. Модели в науке и технике. История, теория, практика. — Л.: Наука, 1984. -190 с.
- Орлов А. И. Менеджмент. Учебник. М.: Издательство «Изумруд», 2003. — 298 с.
- Цветкова Е. Г., Царьков В. В. Решение задачи об управлении обучением студенческого коллектива // Молодой ученый. — 2010. — № 11. Т.1. — С. 40–42.







