Рассмотрим все возможные виды манипуляторов, конечное (рабочее) звено которых имеет шесть степеней свободы в некоторой части пространства.
Обозначим Oxyz координатную систему, связанную со стойкой, а через Nx6y6z6 — систему, связанную с конечным звеном манипулятора. Задание положения полюса N в системе Oxyzможно выполнить поступательными или вращательными парами. Три независимых угла поворота системы Nx6y6z6 относительно Oxyz можно обеспечить только вращательными парами, оси которых не параллельны одной плоскости. Следовательно, среди шести пар манипулятора должно быть не менее трех вращательных.
Количество разновидностей манипуляторов с тремя вращательными парами и тремя поступательными парами равно числу сочетаний из шести элементов по три С63=20. Аналогично подсчитывается количество разновидностей манипуляторов с двумя поступательными парами (С62=15) и одной поступательной парой (С61=0). С шестью вращательными парами возможно только одно сочетание. Следовательно, всего можно получить 42 разновидности манипуляторов, конечное звено которых имеет шесть степеней свободы. Внутри каждого вида можно получить множество модификаций, связанных с различными направлениями осей вращательных пар относительно смежных звеньев и различными направлениями поступательного движения звеньев.
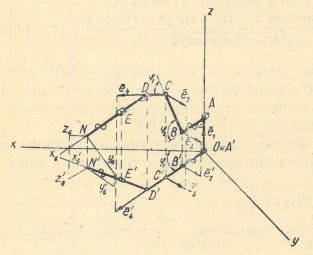
Рис. 1. Кинематическая схема манипулятора вида ВП3ВП-1
Обозначим манипуляторы с шестью вращательными парами символом 6В. Манипулятор с чередующими вращательными и поступательными парами обозначим ВПВПВП. Аналогично обозначаются остальные сорок видов манипуляторов.
На рис. 1 изображена в аксонометрии кинематическая схема манипулятора вида ВП3ВП-1. Стойка представлена координатными осями Oxyz и является первым звеном манипулятора. Второе звено ОА образует со стойкой первую вращательную пару, вдоль оси которой направлен орт 
и ось Oz; точка А расположена на оси Oz. Третье звено (АВ, 
) образует со вторым звеном первую поступательную пару, обеспечивающую изменение длины отрезка АВ, перпендикулярного к оси Oz. Четвертое звено (ВС, ) образует с третьим вторую вращательную пару, вдоль оси которой направлен орт , перпендикулярный к , АВ, ВС. Пятое звено (CD, 
) составляет с четвертым третью вращательную пару, вдоль оси которой направлен орт , перпендикулярный к ВС и CD. Шестое звено (DE, 
) образует с пятым четвертую вращательную пару, вдоль оси которой направлены отрезок CDи орт, перпендикулярный к DE. Седьмое звено (EN, x6y6z6) образует с шестым вторую поступательную пару, обеспечивающую перемещение точки N по прямой DE. Ось Nx6 расположена на прямой EN, ось Nz6 параллельна орту , а ось Ny6 направлена так, чтобы получилась правая прямоугольная координатная система Nx6y6z6.
Постоянными параметрами данного манипулятора являются указанные условия относительного расположения отрезков и ортов, а также длины звеньев: 
. Механизм имеет шесть независимых переменных параметров: 
— угол поворота второго звена относительно стойки; 
— длина отрезка АВ; 
— угол поворота четвертого звена относительно третьего; 
— угол поворота пятого звена относительно четвертого; 
— угол поворота шестого звена относительно пятого; 
— длина отрезка EN. Кроме того, рассмотрим шесть переменных параметров конечного звена: три координаты точки N и три независимых угла 
, 
, 
поворота конечного звена вокруг полюса N.
Для исследования манипулятора используем графоаналитический метод.
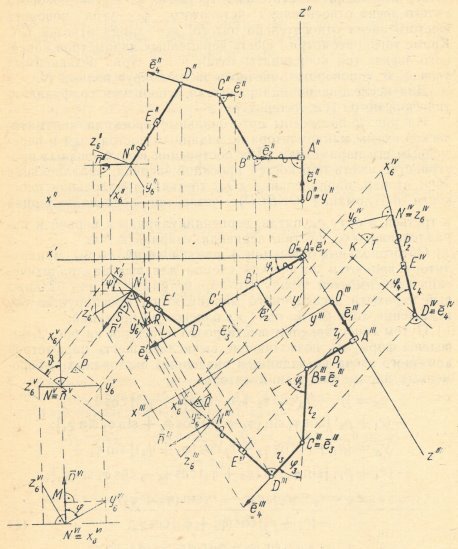
Рис. 2. Ортогональные проекции кинематической схемы манипулятора
На рис. 2 построены ортогональные проекции кинематической схемы манипулятора по заданным постоянным и переменным его параметрам. Для построений использованы в пространстве шесть плоскостей проекций: первая, параллельная xOy; вторая, параллельная xOz; третья, параллельная плоскости 
(ломаная OABCD); четвертая, перпендикулярная к третьей и орту ; пятая, перпендикулярная к первой и параллельная Nx6; шестая, перпендикулярная к Nx6.
Ортогональные проекции кинематической схемы манипулятора являются логической схемой для вывода аналитических зависимостей между его параметрами. На рис. 2 каждый параметр исследуемого манипулятора проецируется без искажения хотя бы на одну из плоскостей проекций.
Путем сопоставления шести полей проекций на рис. 2 выведены формулы, позволяющие вычислить шесть параметров конечного звена по заданным значениям постоянных и переменных параметров манипулятора:
(1)
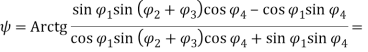
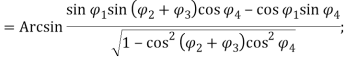
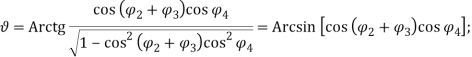
(2)
Определим переменные параметры , , , , , по заданным постоянным параметрам и значениям шести параметров конечного звена манипулятора.
По одному из условий ось Nz6 параллельна орту , расположенному в плоскости ломаной OABCD. Направление оси Nz6 зависит от углов , , , а каноническое уравнение прямой Nz6 имеет вид
Из параллельности плоскости и прямой Nz6 выводим уравнение плоскости
(3)
Точка D расположена на пересечении плоскости
с прямой Nx6, уравнение которой имеет вид
(4)
Обозначим приравненные здесь отношения буквойt. С помощью этого вспомогательного параметра решим систему трех уравнений (3) и (4) относительно x, y, z, в результате определим координаты точки D:
где
(5)
Из уравнения (3), которому удовлетворяют координаты точки D, получаем
(6)
Формула (6) однозначно определяет угол
в пределах его изменения от — 180° до 180°.
Вычисляя длину отрезка ND по формулам (5), получаем
(7)
Точка С расположена в плоскости на прямой, проходящей через точку D и параллельной оси Nz6. Принимая, что длина отрезка CD равна постоянному параметру 
, получаем формулы для вычисления координат точки С
(8)
По первому и третьему полям проекций на рис. 2 составляем следующие уравнения:
(9)
Отметим, что в любом положении данного манипулятора 
; на рис. 2 
.
В результате решения уравнений (9) относительно двух неизвестных переменных параметров и получаем
(10)
По третьему полю проекций устанавливаем связь между углами и и углом, составленным осью Nz6 с осью Oz:
И далее получаем уравнение для вычисления переменного параметра
(11)
Переменный параметр является углом между вектором 
и плоскостью . Если расположен по одну сторону от плоскости , то 
, а если — по другую, то 
. На рис. 2 угол . Этот угол проецируется без искажения на четвертую плоскость проекций и выражается формулой
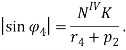
Здесь 
и представляет собой расстояние от точки N до плоскости в пространстве. Это расстояние можно вычислить с помощью уравнения плоскости (3) и координат точки N. Преобразуем уравнение (3) плоскости к нормальному виду:
откуда
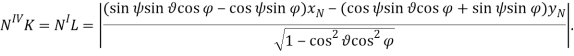
Принимая во внимание конкретные значения параметров на рис. 2, получаем
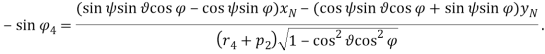(12)
При этом
, если 
, и
, если 
. Это замечание и формула (12) позволяют определить единственное значение в интервале его изменения от — 180° до 180°.
На основании выведенных формул можно программировать и автоматизировать работу описанного манипулятора.
Литература:
- Ананов Г. Д. Кинематика пространственных шарнирных механизмов сельскохозяйственных машин. М. — Л., Машгиз, 1963.
- Поезжаева Е. В. Промышленные роботы: учеб.пособие: в 3 ч. — Пермь: Изд-во Перм. гос. тех. ун-та,2009. — Ч. 2. — 185 с. 2.
