Во многих подлежащих роботизации производственных операциях требуется наряду с выполнением заданного перемещения рабочего органа манипуляционного робота ещё оказывать на обрабатываемый объект заданное силовое воздействие. Существует метод гибридного (по положению и силе) управления манипуляционными роботами, позволяющий одновременно выполнять позиционные задания в одних направлениях и силовые в других. Одним из недостатков этого метода является то обстоятельство, что синтез управления строится на основе только кинематических характеристик манипулятора без учета его динамики. Ниже прилагается метод гибридного управления, основанный на использовании динамических характеристик манипулятора и ограничений на движение рабочего органа [1].
Ограничения на движение рабочего органа могут быть представлены множеством гиперповерхностей в пространстве положений рабочего органа (в дальнейшем под «положением» будет пониматься одновременно и положение и ориентация). Положение рабочего органа представляется в неподвижной декартовой системе координат (эталонной системе) шестимерным вектором ![]() [2]. Предполагается, что ограничения на перемещения рабочего органа заданы набором m гиперповерхностей:
[2]. Предполагается, что ограничения на перемещения рабочего органа заданы набором m гиперповерхностей:
![]() ,
, ![]() ,(1)
,(1)
Взаимно независимых в S подмножестве ![]() . Предполагается, что
. Предполагается, что ![]() и
и ![]() — дважды дифференцируемы по r. Дифференцируя (1) по времени, можно получить:
— дважды дифференцируемы по r. Дифференцируя (1) по времени, можно получить:
![]() (2)
(2)
где
![]() (3)
(3)
![]() (4)
(4)
Вектор ![]() — единичный вектор, нормальный к поверхности
— единичный вектор, нормальный к поверхности ![]() . В связи с предположением о независимости гиперповерхностей ранг
. В связи с предположением о независимости гиперповерхностей ранг ![]() равен m. Из (2) можно получить:
равен m. Из (2) можно получить:
![]() (6)
(6)
Выбирается система векторов {![]() }, таких, что векторы
}, таких, что векторы ![]() ,
, ![]() имеют единичную длину, являются дифференцируемыми функциями r, взаимно независимы и независимы от {
имеют единичную длину, являются дифференцируемыми функциями r, взаимно независимы и независимы от {![]() }. Тогда координатная система с началом в текущем положении органа r с базисом {
}. Тогда координатная система с началом в текущем положении органа r с базисом {![]() } называется координатной системой ограничений (эта система не обязательно ортогональна). Матрица
} называется координатной системой ограничений (эта система не обязательно ортогональна). Матрица ![]() представляет координатные оси, нормальные к поверхности ограничения;
представляет координатные оси, нормальные к поверхности ограничения; ![]() представляет координатные оси, дополнительные к
представляет координатные оси, дополнительные к ![]() , и
, и ![]() является матрицей вращения из неподвижной декартовой системы координат в координатную систему ограничений. На рис. 1 в качестве примера схематически показан манипулятор с двумя степенями подвижности [3–4].
является матрицей вращения из неподвижной декартовой системы координат в координатную систему ограничений. На рис. 1 в качестве примера схематически показан манипулятор с двумя степенями подвижности [3–4].
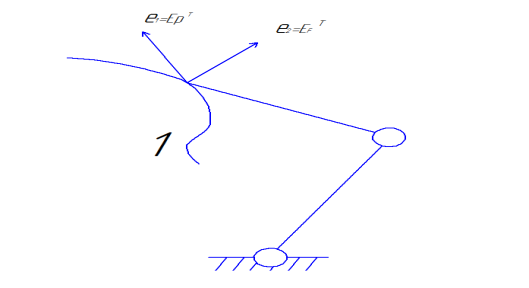
Рис. 1. Манипулятор с двумя степенями подвижности
Где: 1 — поверхность ограничения; ![]() определяет нормальный вектор, а
определяет нормальный вектор, а ![]() — тангенциальный, по направлениям которых могут быть указаны искусственные ограничения соответственно на положение и силу.
— тангенциальный, по направлениям которых могут быть указаны искусственные ограничения соответственно на положение и силу.
Скорость ![]() и ускорение
и ускорение ![]() в координатной системе ограничений определяются выражениями:
в координатной системе ограничений определяются выражениями:
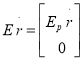 (7)
(7)
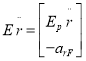 (8)
(8)
В уравнениях (7 и 8) используется тот факт, что нормальная компонента скорости движения рабочего органа равна нулю, а нормальная компонента ускорения определяется только скоростью![]() .
.
Скорость движения рабочего органа
![]() (9)
(9)
где Т — матрица преобразования, является функцией r; предполагается что Т на множестве S не выражена. Представление ограничений ![]() может быть неединственным. Тогда функция
может быть неединственным. Тогда функция ![]() можно выбрать таким образом, чтобы упростить дальнейшие вычисления. В частности, желательно, чтобы {
можно выбрать таким образом, чтобы упростить дальнейшие вычисления. В частности, желательно, чтобы {![]() } были взаимно ортогональны.
} были взаимно ортогональны.
Рассматриваются два типа ограничивающих гиперповерхностей: двухсторонние и односторонние. Односторонние поверхности запрещают движение в одном направлении по отношению к поверхности, в то время как движение в другом направлении разрешено. Двухсторонние поверхности запрещают покидать поверхность в любом направлении. В дальнейшем рассматриваются исключительно задания, в которых рабочий орган находится в контакте с поверхностью и прикладывает к ней заданную силу и в связи с этим оба варианта поверхностей не различаются [6].
Теперь рассмотрим манипулятор с n степенями подвижности, перемещения в сочленениях ![]() . Предполагается, что векторы r и q связаны соотношением:
. Предполагается, что векторы r и q связаны соотношением:
![]() (10)
(10)
Тогда:
![]() ,
, ![]() (11)
(11)
![]() ,
, ![]() (12)
(12)
Динамика манипулятора может быть представлена уравнением:
![]() (13)
(13)
где
![]() (14)
(14)
Шестимерный вектор обобщенной силы, соответствующий обобщенной скорости v задан компонентами силы, действующей вдоль осей эталонной координатной системы, и компонентами момента относительно этих осей. Для упрощения анализа трение между ограничивающей поверхностью и рабочим органом отсутствует. Тогда в соответствии с принципом виртуальной работы сила ![]() , развиваемая на поверхности рабочим органом, удовлетворяет соотношению:
, развиваемая на поверхности рабочим органом, удовлетворяет соотношению:
![]() (15)
(15)
Литература:
- Поезжаева, Е. В. промышленные роботы: учеб. пособие: в 3 ч. / Е. В. Поезжаева. — Пермь: Изд-во Перм. гос.тех. ун-та, 2009. — Ч.2. — 185 с.
- Зенкевич С. Л. Основы управления манипуляционными роботами / С. Л. Зенкевич, А. С. Ющенко. — М.: Изд-во МГТУ им. Н. Э. Баумана, 2004. — 479 с.
- Корендясев А.И, Саламандра Б.Л, Тывес Л. И. Манипуляционные системы роботов. М.: Машиностроение, 1989. 472 с.
- Разработка концепции адаптивного отслеживания шва в реальном времени для роботизированной сварки. Поезжаева Е. В., Сергеев А. А., Мисюров М. Н. Молодой ученый. 2015.№ 16с. 214–218.
- Герасун В. М. Исследование оптимальных конфигураций манипулятора — трипода с поворотным основанием / В. М. Герасун, В. В. Жога, И. А. Несмиянов, Н. С. Воробьева, В. В. Дяшкин-Титов // Мехатроника, автоматизация, управление, 2013. — № 6. — С. 21–16.
- Довбня Н. М. Роботизированные технологические комплексы в ГПС / Н. М. Довбня, А.Н Кондратьев, Е. И. Юревич. М., 2000.







