При расчетах процессов переработки природного газа наиболее важной и трудной задачей является расчет фазового равновесия жидкость — пар. При этом требуется определить состав фаз и их количество. В смесях, содержащих воду, метанол, гликоли, возможно выделение второй жидкой фазы.
Равновесие жидкость — пар
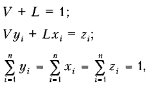
Запишем уравнения материального баланса для одного моля смеси и каждого компонента:
где V — мольная доля газовой фазы; L — мольная доля жидкой фазы; уi — мольная доля г компонента в газовой фазе; хi -мольная доля г компонента в жидкой фазе; zi — мольная доля г компонента в смеси.
Распределение компонентов между фазами наиболее часто выражают через константы фазового равновесия:
![]()
Решая эти уравнения методом последовательных приближений, получают составы фаз и доли паровой и жидкой фаз в смеси.
Чтобы избежать лишних вычислений следует сначала убедиться, что смесь при данных условиях находится в двухфазном состоянии. Для этого рекомендуется предварительно вычислить следующие функции:
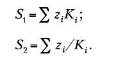
Если S1 и S2 больше единицы, то смесь находится в двухфазном состоянии, если S1 меньше единицы, то одна жидкая фаза, если S2 меньше единицы, то одна газовая фаза. Точка росы соответствует S2 = 1, точка начала кипения — S2 = 1.
Константы фазового равновесия зависят от температуры, давления и состава фаз. Современные методы расчета констант фазового равновесия основаны на строгих термодинамических соотношениях и уравнениях состояния.
Условиями фазового равновесия являются равенство температур, давлений и химических потенциалов всех компонентов в каждой из фаз. Для практических расчетов более удобной является функция — летучесть f, эквивалентная химическому потенциалу.
![]()
Разделим летучести г компонента в паровой и жидкой фазах на давление и мольную долю компонента:
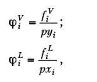
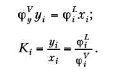
Коэффициент летучести i компонента в смеси может быть определен по следующему термодинамическому уравнению:
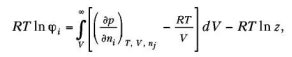
где ni — количество молей i компонента в смеси; z коэффициент сжимаемости смеси.
Для вычисления коэффициентов летучести по уравнению используют уравнения состояния, которые связывают между собой давление, температуру, объем и состав смеси.
Летучесть чистой жидкости в стандартном состоянии может быть вычислена по корреляциям, основанным на принципе соответственных состояний, или по уравнениям состояния.
Для вычисления коэффициентов активности применяются эмпирические или полуэмпирические уравнения, удовлетворяющие уравнению Гиббса — Дюгема:
Выражения получены при использовании уравнений, но можно также использовать уравнение. Это зависит от того, какие константы равновесия определены. Для определения составов всех фаз и их количеств достаточно иметь два любых набора констант фазового равновесия.
В уравнениях, используя уравнение, можно исключить одну из величин V, L или W.
Решение приведенных уравнений с целью определения составов фаз и их числа производится методом последовательных приближений.
Другой способ расчета трехфазного равновесия заключается в последовательном расчете двухфазного равновесия. Например, сначала рассчитывается равновесие пар — углеводородная жидкость, затем пар — водная жидкость, после чего все повторяется. Расчет продолжается до тех пор, пока не установятся постоянные величины V, L, W и составы фаз. Этот способ показал довольно быструю и надежную сходимость.
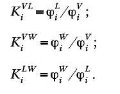
Из уравнений можно получить
Для расчета коэффициентов летучести используются уравнения состояния. Наибольшее применение для расчета фазовых равновесий в смесях углеводородов получили уравнения Бенедикта — Вебба — Рубина (БВР) [1], Старлинга — Хана [2], Соава [3].
В настоящее время преимущество отдается двум последним, так как они значительно проще, более универсальны, легче поддаются модификации для включения неуглеводородных веществ и расчета трехфазного равновесия.
Все указанные уравнения и их применение для расчета коэффициентов летучести и других свойств достаточно полно описаны в [3].
Рассмотрено уравнение состояния Пател — Тея [2], которое является обобщающим по отношению к уравнениям Соава и Пенга — Робинсона и за счет дополнительного параметра позволяет более точно предсказывать плотность тяжелых углеводородов и полярных компонентов.
Литература:
- Бекиров Т. М. Влияние уноса гликоля с установки осушки на показатели работы газотранспортных систем//Подготовка, переработка и использование газа. — М.: ВНИИЭгазпром, 1980. — № 11. — С. 9–11.
- Бекиров Т. М. Первичная переработка природных газов. — М.: Химия, 1987.- 256 с.
- Бекиров Т. М. Системный подход к установлению показателей качества товарного газа//Анализ работы модернизированного оборудования на действующих промыслах и использование современных технологий и оборудования на новых месторождениях Западно-Сибирского региона. — М.: ИРЦ Газпром. — 1996. — С. 74–88.







