О моделях А. Д. Базыкина «хищник — жертва»

 

Дано краткое описание математических моделей «хищник-жертва», исследованных А. Д. Базыкиным. Для конкретных видов трофических функций дан анализ устойчивости стационарных точек. Приведены численные примеры.

Ключевые слова: математическое моделирование, устойчивость, трофические функции, популяции.

 

Введение. Итальянский математик Вито Вольтерра в 1930-е годы в серии своих работ разработал основные положения математической популяционной биологии [11]. При разработке моделей взаимодействующих популяций учитывались процессы, происходящие в биоценозах. Основной из них — взаимоотношение между популяциями, основанное на распределении трофического ресурса между ними. Математические модели строились на основе систем обыкновенных дифференциальных уравнений с использованием принципа парных взаимоотношений для описания скоростей изменения численности популяций. Значительная часть исследований Вольтерра относится не столько к моделированию динамики реальных биологических популяций, сколько непосредственно к решению математических задач. Тем не менее, роль Вольтерра как одного из основных разработчиков математических моделей взаимодействующих популяций, огромна [16, 54]. Последователями Вольтерра были предложены математические модели хищник-жертва, учитывающие их взаимодействие на территории [13, 15, 32, 57, 61, 67, 68], влияние антропогенного давления [17, 25, 27, 36]. Принципы построения математических моделей для взаимодействующих популяций стали применять и в задачах медицины [12, 21, 51, 55, 60, 69], экономики [2, 3, 9, 10, 14, 26, 31, 33, 41, 45, 62] и социальных систем [1, 7, 30, 34, 35, 37, 42].

Новый интерес к задачам популяционной биологии возник в 1960-е годы, поскольку в этот период стали заметны экологические последствия деятельности человека. Возникла необходимость в прогнозе возможных изменений в биосфере, вызванных техногенным воздействием на нее. Накопленные данные полевых наблюдений зачастую не вписывались в разработанные к тому времени математические модели. Одним из значимых исследований стала работа А. Н. Колмогорова [28]. В отличие от используемого Вольтерра принципа парных взаимоотношений в ней был предложен иной подход для описания межпопуляционных взаимодействий — предлагалось в математические модели вводить трофические функции общего вида, качественно отражающие характер взаимодействия, как между популяциями, так и внутри популяций. Одним из последователей этого подхода стал А. Д. Базыкин. Результаты его исследований изложены в монографии [6].

Модель хищник-жертва Лотки-Вольтерра. В этой математической модели предполагается, что рост популяции жертвы в отсутствие хищника происходит по экспоненциальному закону, этому же закону подчиняется и естественная смертность хищника, скорость размножений хищника и скорость гибели жертвы пропорциональны частоте их встреч. Популяции обитают в среде, свойства которой в каждой точке пространства одинаковы. Если  — общая численность жертвы в ареале, а  — численность хищника, то модель их взаимодействия представлена системой дифференциальных уравнений

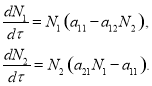(1)

, , ,  — константы.

Эта система заменой переменных [6]

, ,

приводятся к системе уравнений

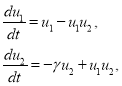
содержащей только один параметр .

Эта система уравнений имеет неустойчивую стационарную точку и и устойчивую и , являющуюся центром [5]. В малой окрестности этой точки происходят колебания с частотой . Все траектории этой системы образуют замкнутые циклы [6].

Модель Вольтерра не учитывает множества особенностей в поведении как отдельных особей в популяции, так и самой популяции как единого целого. Она не согласуется и со множеством данных полевых наблюдений [8, 43]. Однако она является и по сегодняшний день эталонной, поскольку на сновании нескольких очевидных предположений объясняет одну из причин периодичности изменения численности популяций.

Модели А. Д. Базыкина. После опубликования работы А. Н. Колмогорова [28] происходило дальнейшее развитие моделей Вольтерра. А. Д. Базыкин предложил свой вариант модели хищник-жертва [6], близкий по форме к модели А. Н. Колмогорова [28], и исследовал решения для различных трофических функций. Обобщенная модель А. Д. Базыкина представлена системой дифференциальных уравнений

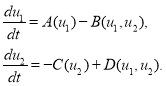
В этих уравнениях функция описывает динамику жертвы в отсутствие хищника, функция  — динамику гибели хищника в отсутствие жертвы, функция  — скорость уничтожения жертвы хищником, функция  — скорость увеличения численности хищника за счет переработки им жертвы.

Функция обращается в ноль при , а функция  — при . Предполагается, что при или функции и не отрицательные и не убывающие функции своих аргументов, обращающиеся в ноль при или . С учетом этого в [6] предлагается считать, что , а ( — постоянная). При этом и . С учетом этих условий в окрестности точки , функции , и раскладываются в ряд по степеням своих аргументов

,

,

.

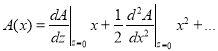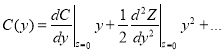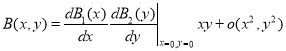В модели Вольтерра (1) . То есть численность жертвы в отсутствие хищника растет по экспоненциальному закону. А это не согласуется с полевыми наблюдениями [8] — ни одна популяция в историческом масштабе не достигла огромных размеров. С другой стороны и численность малочисленной популяции возникшей в каком-то месте на начальном этапе ее эволюции растет. Поэтому в окрестности точки функция должна быть возрастающей, но ограниченной сверху при . Этому условию удовлетворяет функция .

Скорость гибели хищника в отсутствие жертвы должна быть пропорциональной его численности. Поэтому квадратичным слагаемым в разложении функции в ряд по малому параметру можно в первом приближении пренебречь и считать, что .

Таким образом, в [6] основная модель хищник-жертва, обобщающая модель А. Н. Колмогорова [28], представлена системой уравнений

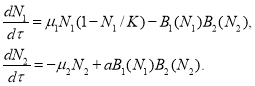
Эта система уравнений заменой переменных , , , , приводится к виду

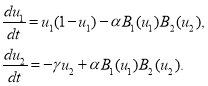(2)

Разработанная в [6] модель в отличие от модели Вольтерра (1) учитывает дополнительные факторы, влияющие на реальные системы хищник-жертва: нелинейность скорости размножения жертвы и конкуренцию внутри ее популяции, эффект насыщения хищника жертвой, конкуренцию хищников за жертв, нелинейный характер уничтожения жертвы хищником и иные эффекты [6].

Стационарные точки. Система уравнений (2), поскольку и , имеет стационарные точки

, и , ..(3)

В первой стационарной точке собственными значениями матрицы Якоби правой части уравнений (2)

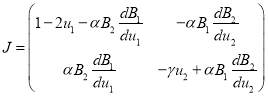
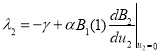будут и . Поэтому, поскольку эта стационарная точка будет неустойчивой. Во второй стационарной точке собственными значениями матрицы Якоби будут и . Поскольку функция положительно определенная, а не убывающая функция, то будет отрицательной величиной при выполнении неравенств 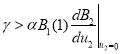и вторая стационарная точка в этом случае будет устойчивой.

Остальные стационарные точки находятся как решение системы алгебраических уравнений

(4)

Значение в стационарной точке определяется из второго уравнения в (4) по найденному значению из уравнения

.

Поскольку и , то это уравнение имеет как минимум два корня:

и . В точке

,

а в точке

.

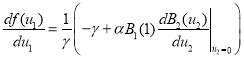Таким образом, в окрестности точки функция является положительной и возрастающей. А в окрестности точки функция будет принимать отрицательные значения и будет возрастающей при выполнении неравенства

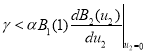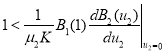или .(5)

Это неравенство при условии, что 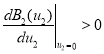, является условием существования стационарной точки, в которой .

При малых значениях параметра или больших значения параметра неравенство (5) может не выполняться. Тогда система уравнений (4) будет иметь только стационарные точки (3), при этом будет устойчивой только стационарная точка , . Это означает, что в рамках модели (2) при малых скоростях потребления (или переработки) хищником жертвы (малые значения ) или при высокой смертности хищника по сравнению с рождаемостью жертвы (большие значения ), хищник может погибнуть. При этом, поскольку параметр обратно пропорционален емкости среды, то выживаемость хищника с ростом емкости среды жертвы обеспечивается и ростом скоростью переработка хищником жертвы.

Трофические функции. В качестве трофических функций хищника, удовлетворяющих изложенным выше условиям, в [6] использовались рациональные функции

, , ,

и, соответственно

(),

 — константа.

Для случая функции

«не тривиальные» корни уравнения (4) удовлетворяют кубическому уравнению

, (6)

которое на промежутке может, как не иметь вещественных корней, так и иметь один или три вещественных корня. Для случая , , на рис. 1 отражена зависимость корней уравнения (6) от параметра .

Собственные значения матрицы Якоби правой части уравнений в устойчивых стационарных точках могут быть как отрицательными, так и комплексно сопряженными с отрицательной вещественной частью. В окрестности стационарных точек с малыми значениями и при больших значениях параметра (при больших скоростях уничтожения жертвы хищником) могут возникать колебания. На рис. 2 для случая отражена зависимость функций и от времени (,). При этом значении параметра система уравнений (4) имеет три стационарные точки, в которых (рис. 1). Рис. 2 соответствуют случаю, когда система из окрестности неустойчивой стационарной точки переходит в окрестность устойчивой стационарной точки (рис. 1 — переход из точки A в точку B). Численное интегрирование осуществлялась в среде математического пакета Matlab с применением встроенных функций [29]. Результаты (рис. 2) получены с относительной и абсолютной точностью равными . При точностях равными (в Matlab это точность по «умолчанию») численные методы, реализованные в , строят периодические колебания (рис. 3).

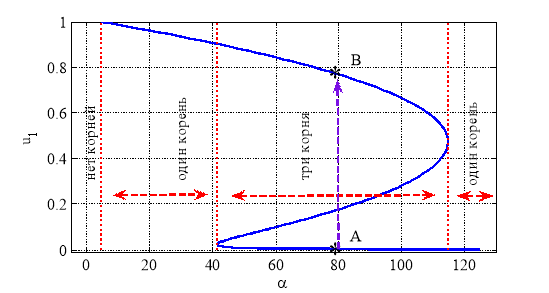
Рис. 1.

 

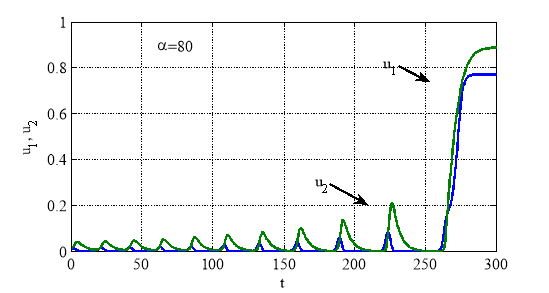
Рис. 2.

 

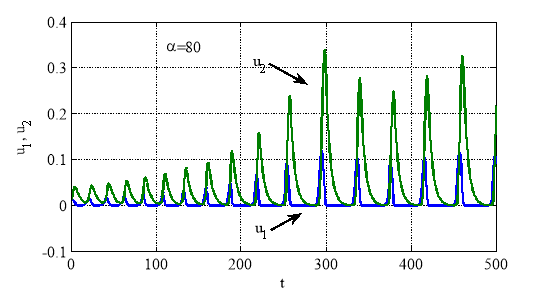
Рис. 3.

 

Для случая функции

«не тривиальные» корни уравнения (4) удовлетворяют уравнению

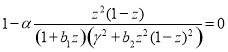,(7)

которое на промежутке может, как не иметь вещественных корней, так и иметь до пяти вещественных корней. Для случая , , на рис. 4 отражена зависимость корней уравнения (7), лежащих на промежутке , от параметра . Собственные значения матрицы Якоби правой части уравнений в устойчивых стационарных точках могут быть как отрицательными, так и комплексно сопряженными с отрицательной вещественной частью.

К какой стационарной точке будет стремиться решение уравнений (2) зависит от выбора начальных данных. Так, например, при значениях (, , ) и начальных данных и решение стремится в стационарную точку , — на рис. 4 отражена зависимость функций и от времени.

Трофические функции у взаимодействующих популяций могут изменяться под влиянием внешних факторов. Это может быть изменение внутреннего метаболизма особей, изменение пространственного распределения популяций, изменение свойств среды обитания под влиянием антропогенного давления. Антропогенная нагрузка может привести к изменению качества трофических ресурсов или к их уничтожению [18, 40. 46-49, 56, 63-65], к физическому поражению особей. В моделях, исследованных в [6], не учитывалась, что трофические функции могут изменяться во времени. Учет этого фактора в моделях взаимодействующих популяций позволяет объяснить более широкий спектр явлений, наблюдаемых в природе. Временной фактор можно учесть, считая что , , и в уравнениях (2) является не параметрами, а функциями времени. Для случая (значение из области «два корня» со временем приближается к области «четыре корня», рис. 4), на рис. 6 отражена зависимость функций и от времени (, , , , ). Этот результат соответствуют случаю, когда после длительного совместного существования хищника и жертвы на первый взгляд устойчивого (рис. 5 — зона «иллюзия» устойчивости, [20, 52, 53, 66]) численность обеих популяций резко уменьшается. При этом хищник погибает, а жертва постепенно восстанавливает свою численность (рис. 5).

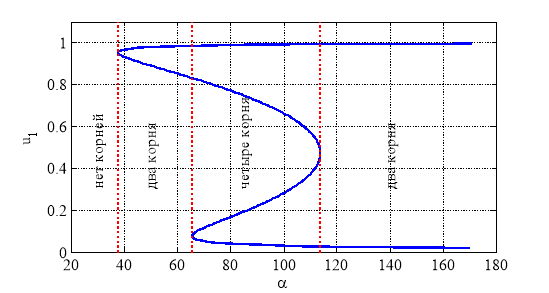
Рис. 4.

 

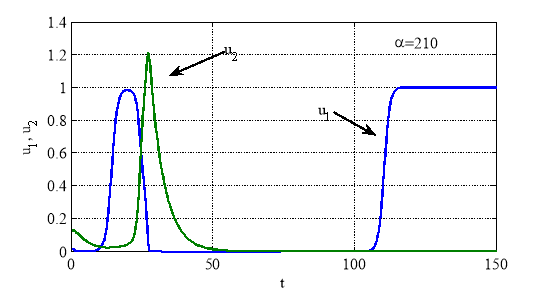
Рис. 5.

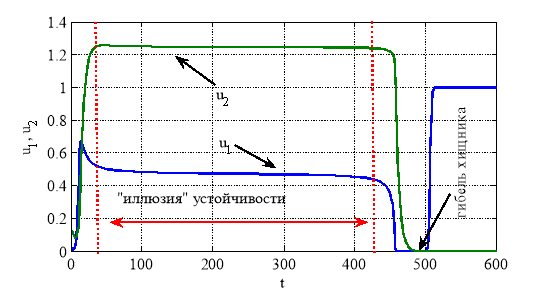
Рис. 6.

 

В общем случае найти точные значения координат стационарных точек и собственных значений матрицы Якоби правой части разрешающий системы дифференциальных уравнений не представляется возможным [4]. Для решения этих задач приходится использовать численные методы поиска корней нелинейных трансцендентных уравнений. При наличии нескольких стационарных точек переход из окрестности одной стационарной точки в окрестность другой может сопровождаться резким изменением амплитуды решения [19, 22, 38]. В этом случае для решения задачи Коши для обыкновенных дифференциальных уравнений приходится использовать методы, предназначенные для решения задач такого рода [44, 50]. Отдельной задачей является и задача построения бифуркационных ветвей решений дифференциальных уравнений [23, 24, 39, 44, 58, 59].

Заключение. Математические модели хищник-жертва, предложенные в работах А. Д. Базыкина, объясняют существование нескольких стационарных состояний в системе хищник жертва как устойчивых, так и не устойчивых. Одновременно с этим объясняют и возможное «резкое» исчезновение хищника. Основными факторами, определяющими, соотношение численностей, являются удельная скорость роста жертвы, удельная скорость гибели хищника, скорость уничтожения жертвы хищником и скорость переработки жертвы хищником.

 

Литература:

 

1.                Аббасов М. Э. О. Условия экстремума в терминах несобственных экзостеров∗) // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2011. — № 2. — С. 3-8.
2.                Абдулина К. А., Старков В. Н. Качественное исследование динамики лесной системы с учетом вырубки и вывоза // Процессы управления и устойчивость. — 2014. — Т. 1. — № 1. С. 82-86.
3.                Абдулина К. А., Старков В. Н.Квазистационарный подход в исследовании распространения насекомых в лесной системе // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 5-15.
4.                Александров А. Ю., Александрова Е. Б., Платонов А. В. Анализ устойчивости положений равновесия нелинейных механических систем с нестационарным ведущим параметром при потенциальных силах // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 107-119.
5.                Александров А. Ю., Платонов А. В.О предельной ограниченности и перманентности решений одного класса дискретных моделей динамики популяций с переключениями// Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 1. — С. 5-16.
6.                Базыкин А. Д. Нелинейная динамика взаимодействующих популяций. Москва-Ижевск: Институт компьютерных технологий, 2003. — 368 с.
7.                Басков О. В. Критерий непротиворечивости «квантов» информации о нечетком отношении предпочтения лица, принимающего решения // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 2. — С. 12-18.
8.                Бигон М., Харпер Дж., Таунсенд К. Экология. Особи, популяции и сообщества: в двух томах. М.: Мир, 1989. Т. 1. 667 с. Т. 2. 477 с.
9.                Буре А. В. Об одной теоретико-игровой модели тендера // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 25-32.
10.            Валиотти Н. А. Нейросетевая модель для дифференцированной оценки влияния одновременных внешних событий в сфере розничной торговли // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 2. — С. 93-98.
11.            Вольтерра В. Математическая теория борьбы за существование. Москва-Ижевск:, Институт компьютерных технологий, 2004. — 288 с.
12.            Гасратова Н. А., Бойцов Д. С., Габриелян Л. А., Тюганова Т. М. Математическая модель иммунного ответа организма млекопитающих на поражение кожи ожогом // Молодой ученый. — 2014. — № 12 (71). — С. 1-7.
13.            Гасратова Н. А., Бойцов Д. С., Крылова В. А., Гаврилова А. В. Модель Базыкина-Свирежева хищник-жертва // Молодой ученый. — 2014. — № 12 (71). — С. 8-12.
14.            Гасратова Н. А., Гасратов М. Г. Сетевая модель управления запасами для случая количественной конкуренции // Сибирский журнал индустриальной математики. — 2015. — Т. 18. — № 1. — С. 14-27.
15.            Гасратова Н. А., Столбовая М. В., Бойцов Д. С., Степанова Д. С. Математическая модель хищник-жертва на линейном ареале // Молодой ученый. — 2014. — № 11. — С. 1-10.
16.            Гиляров А. М. В поисках универсальных закономерностей организации сообществ: прогресс на пути нейтрализма // Журнал общей биологии. — 2010. — Т. 71. — № 5. — С. 386–401.
17.            Горбунова М. В., Колпак Е. П., Крицкая А. В. Математическая модель антропогенного воздействия на одиночную популяцию / В сборнике: Синергетика в общественных и естественных науках: девятые Курдюмовские чтения материалы Международной междисциплинарной научной конференции с элементами научной школы для молодежи. редкол.: Лапина Г. П. (отв. ред.) и др. Тверь, 2013. — С. 165.
18.            Даль Ю. М., Пронина Ю. Г. Сосредоточенные силы и моменты у границы упругой полуплоскости // Известия Российской академии наук. Механика твердого тела. — 1998. — № 5. — С. 78.
19.            Жабко А. П., Мышков С. К. К вопросу об асимптотической устойчивости линейных нестационарных систем // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 2. — С. 166-175.
20.            Жук В. В., Тумка О. А., Козлов Н. А.О константах в неравенствах типа Джексона для наилучших приближений периодических дифференцируемых функций// Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 33-41.
21.            Жукова И. В., Колпак Е. П.Математические модели злокачественной опухоли // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 3. — С. 5-18.
22.            Золотых М. С., Моисеев И. АСвойства точек переключения управления нелинейной системы четвертого порядка // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления — 2014. — № 3. — С. 118-124.
23.            Кабриц С. А. Некоторые прикладные задачи статики тонких оболочек из эластомеров // диссертация на соискание ученой степени кандидата физико-математических наук / Ленинград, 1984.
24.            Кабриц С. А., Шамина В. А. Изгиб оболочки вращения поперечной силой и моментом // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2014. — № 2. — С. 261-270.
25.            Камачкин А. М., Старков В. Н., Степенко Н. А. Математическая модель загрязнения океанических вод // Вестник Тамбовского университета. Серия: Естественные и технические науки. — 2015. — Т. 20. — № 2. С. 475-479.
26.            Колабутин Н. В. Двухуровневая кооперация в дифференциальной игре технологического альянса // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 42-63.
27.            Колесин И. Д., Старков В. Н., Гасратова Н. А. Одиночная популяция под антропогенным давлением // Журнал научных публикаций аспирантов и докторантов. — 2014. — № 6 (96). — С. 226-232.
28.            Колмогоров А. Н. Качественное изучение математических моделей динамики популяций // Проблемы кибернетики. — 1972. — № 5. — С. 101-106.
29.            Колпак Е. П. Mathlab: методы вычислений учебное пособие / Е. П. Колпак; Санкт-Петербургский гос. ун-т. Санкт-Петербург, 2007.
30.            Колпак Е. П., Бронникова А. И., Полежаев В. Ю. Математическая модель стачечного движения в России в начале XX века // Молодой учёный. — 2015. — № 3 (83). — С. 4-15.
31.            Колпак Е. П., Габриелян Л А., Бронникова А. И., Крылова В. А. О математических моделях симбиоза // Молодой ученый. — 2015. — № 4 (84). — С. 6-14.
32.            Колпак Е. П., Гасратова Н. А., Селицкая Е. А. Математическая модель хищник-жертва на ограниченной территории // В сборнике: Устойчивость и процессы управления Материалы III международной конференции. — 2015. — С. 481-482.
33.            Колпак Е. П., Горыня Е. В., Крылова В. А., Полежаев Д. Ю. Математическая модель конкуренции двух популяций на линейном ареале // Молодой ученый. — 2014. — № 12 (71). — С. 12-22.
34.            Колпак Е. П., Селицкая Е. А., Габриелян Л. А. Математическая модель коррупции в системе «власть-общество» // Молодой ученый. — 2015. — № 10 (90). — С. 9-16.
35.            Колпак Е. П., Скороходова Т. В. Математическая модель роста числа учащихся в средней и высшей школах России. В сборнике: Синергетика в естественных науках. Восьмые Курдюмовские чтения материалы Международной междисциплинарной научной конференции с элементами научной школы для молодежи. Ответственный редактор: Лапина Г. П.. Тверь, 2012. С. 274-275.
36.            Колпак Е. П., Столбовая М. В., Селицкая Е. А Математическая модель антропогенного давления на популяцию // Приволжский научный вестник. — 2015. — № 10 (50). — С. 5-15.
37.            Крылова В. А., Колпак Е. П., Сыромолотова К. И., Воротова Т. А. Математические модели формирования спортивных групп // Молодой учёный. — 2015. — № 8 (88). — C. 10-19.
38.            Лакрисенко П. А. Об устойчивости положений равновесия нелинейных гибридных механических систем // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 3. — С. 116-125.
39.            Мальков В.М., Кабриц С.А., Мансурова С.Е. Математическое моделирование нелинейной деформации эластомерного слоя // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2011. — № 3. — С. 56-63.
40.            Мальков В. М., Малькова Ю. В. Трещина в форме дуги окружности, расположенная вблизи поверхности раздела материалов // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2010. — № 1. — С. 93-104.
41.            Миндлин Ю. Б., Колпак Е. П., Гасратова Н. А. Отличительные признаки кластеров и практика их применения в России // Политика и общество. — 2015. — № 5. — С. 666-675.
42.            Морозова Н. С. Виртуальные формации и виртуальные лидеры в задаче о движении строем группы роботов // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 135-149.
43.            Окулова Н. М., Катаев Г. Д. Взаимосвязи "хищник-красно-серая полевка" в сообществах позвоночных животных Лапландского заповедника // Зоологический журнал. — 2007. — Т. 86. — № 8. — С. 989 — 998.
44.            Олемской И. В., Фирюлина О. С. Алгоритм поиска наибольшего независимого множества // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 1. — С. 79-89.
45.            Полякова Л. Н., Карелин В. В., Буре В. М., Хитров Г. М. Точные штрафные функции в задаче управления одной системой массового обслуживания // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 75-82.
46.            Пронина Ю. Г Механохимическая коррозия полого цилиндра из идеального упруго-пластического материала под действием постоянного давления // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2006. — № 3. — С. 121-130.
47.            Пронина Ю. Г.Оценка устойчивости упругой трубы под давлением коррозионных сред // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2006. — № 3. — С. 55-63.
48.            Пронина Ю. Г.Равномерная механохимическая коррозия полой сферы из идеального упругопластического материала под действием постоянного давления // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2009. — № 1. — С. 113-122.
49.            Пронина Ю. Г. Расчет долговечности упругой трубы под действием продольной силы, давления и осесимметричного нагрева в условиях равномерной коррозии // Проблемы прочности и пластичности. — 2009. — № 71. — С. 129-135.
50.            Слупко К. А.Периодические дифференциально-разностные системы. алгоритм построения матрицы Ляпунова// Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 150-159.
51.            Смирнова М. В., Колпак Е. П. Математическое моделирование снижения детской заболеваемости в России // В сборнике: Синергетика в общественных и естественных науках: девятые Курдюмовские чтения. Материалы Международной междисциплинарной научной конференции с элементами научной школы для молодежи. редкол.: Лапина Г. П. (отв. ред.) и др.. Тверь, 2013. — 222 с.
52.            Степенко Н. А. О диссипативности неавтономных систем по нелинейному приближению // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2004. — № 3-4. — С. 160-169.
53.            Степенко Н. А. О некоторых критериях диссипативности колебательных систем с переменными параметрами // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2004. — № 1. — С. 50-54.
54.            Трубецков Д. И. Феномен математической модели Лотки-Вольтерры и сходных с ней // Известия Вузов. Прикладная нелинейная динамика. — 2011. — № 2. — С. 69-87.
55.            Balykina Y. E., Kolpak E. P., Kotina E. D. Mathematical model of thyroid function // Middle East Journal of Scientific Research. — 2014. — Т. 19. — № 3. — С. 429-433.
56.            Dal' Yu. M., Pronina Yu. G. On concentrated forces and moments in an elastic half-plane // ВестникСанкт-Петербургскогоуниверситета. Серия 1: Математика. Механика. Астрономия. — 1998. — № 1. — С. 57-60.
57.            Ge W., Gui z. The effect of harvesting on a predator–prey system with stage structure // Ecological Modelling. — 2005. — Т. 187. — С. 329–340.
58.            Kabrits S. A., Kolpak E. P. Finding bifurcation branches in nonlinear problems of statics of shells numerically // Всборнике: 2015 International Conference "Stability and Control Processes" in Memory of V.I. Zubov (SCP) 2015. С. 389-391.
59.            Kabrits S. A., Kolpak E. P. Numerical study of convergence of nonlinear models of the theory of shells with thickness decrease // Всборнике: AIP Conference Proceedings. — 2015. — С. 300005.
60.            Kolpak E. P., Kabrits S. A., Bubalo V. The follicle function and thyroid gland cancer // Biology and Medicine. — 2015. — Т. 7 (1). — BM060.15.
61.            Murray D. D. Mathematical biology. N.Y. Springer. 2002. — 551 p.
62.            Peresada V. P., Smirnov N. V. E., Smirnova T. E. Development control of a multicommodity economy based on the dynamical input-output model// ВестникСанкт-Петербургскогоуниверситета. Серия 10: Прикладнаяматематика. Информатика. Процессыуправления. — 2014. — № 4. — С. 119-132.
63.            Pronina Y. G. Analytical solution for decelerated mechanochemical corrosion of pressurized elastic-perfectly plastic thick-walled spheres // Corrosion Science. — 2015. — Т. 90. — С. 161-167.
64.            Pronina Y. G. Lifetime assessment for an ideal elastoplastic thick-walled spherical member under general mechanochemical corrosion conditions // Computational Plasticity XII: Fundamentals and Applications — Proceedings of the 12th International Conference on Computational Plasticity — Fundamentals and Applications, COMPLAS 2013. PP. 729-738.
65.            Pronina Y.G., Sedova O.S., Kabrits S.A On the applicability of thin spherical shell model for the problems of mechanochemical corrosion // AIP Conference Proceedings/ — 2015. — vol. 16-48. — art. no. 300008.
66.            Starkov V. N., Stepenko N. A. Computer modeling of trajectories in spatially non-uniform gravitational fields // International conference on computer technologies in physical and engineering applications (IVESC-ICEE-ICCTPEA-BDO 2014). June 30-July 4. 2014, Russia, Saint-Petersburg, pp. 179-180.
67.            Tsoularis A., Wallace J. Analysis of logistic growth models // Mathematical Biosciences. — 2002. — № 179. — P. 21-55.
68.            Wang W., Takeuchi Y.Adaptation of prey and predators between patches // Journal of Theoretical Biology. — 2009. — V. 258. — P. 603-613.
69.            Zhukova I. V., Kolpak E. P., Balykina Yu. E. Mathematical Model of Growing Tumor // Applied Mathematical Sciences. — 2014. — Т. 8. — N 29-32. — С. 1455-1466.