Применение специальных задач для успешного выполнения заданий повышенного уровня единого государственного экзамена

 

This article discusses the most effective method of fulfilling the tasks of higher level of difficulty during the process of preparations for the mathematics unified state exam. This method consists in drawing up special tasks that are considered to be basic in the process of doing tasks of this kind.

Keywords: unified state exam, № 19 USE, specific tasks, optional work in mathematics

 

В связи с введением ЕГЭ как формы государственной итоговой аттестации для получения среднего образования, обучающихся, родителей и педагогов остро волнует вопрос наиболее эффективной подготовки к этому заключительному испытанию основной школы. С первых лет его проведения учителя и методисты предлагают меры интенсивного «подтягивания» для наиболее успешного преодоления подобного экзамена. Анализ методической литературы и практика ЕГЭ показали, что данная форма проверки знаний требует четко организованного системного повторения изученного материала и более глубокого усвоения отдельных тем.

Обычно особую трудность ученики испытывают при решении заданий повышенного уровня, в частности, последних заданий части 2, поскольку их отличает ярко выраженный нестандартный характер. Информация, необходимая для поиска правильного ответа, может относиться к различным разделам школьного курса математики, например, последовательности и прогрессии, сюжетные задачи, числа и их свойства. Построение решения таких заданий будет осуществляться быстро и безболезненно, если организовывать подготовку к ЕГЭ путем ознакомления учащихся со специальными задачами. Под специальными задачами будем понимать совокупность задач, содержащих формулы, факты, алгоритмы, методы, использование которых приводит к эффективному решению поставленной задачи повышенного уровня (2 части экзамена) [2]. Так в литературе[2]приводятся такие специальные задачи (рис. 1):

Рис.1. Специальные задачи из литературного источника [2]

 

Приведем примеры заданий второй части ЕГЭ 2016 (№ 19) и покажем, каким образом осуществляется их решение на основе специальных задач.

Задача 1. У натурального числа N равно 6 делителей. Их сумма равна 3500. Найдите число N [3].

Решение: По условию известно, что число имеет 6 делителей, следовательно, необходимо рассмотреть два случая:

1)                 Используя спецзадачи № 4 и № 5, представим число N в виде . По специальной задаче № 6 находим сумму его делителей

. Аналогично разложим число3500 на множители: . Значит, принадлежит множеству делителей числа 3500: . Учитывая спецзадачу № 1 и факт, что  — простое число, делаем вывод: , остальные значения являются составными числами. Теперь должны рассмотреть квадратные уравнения вида

при . Его дискриминант равен и должен быть полным квадратом. Данное условие выполняется только при k= 7, и . Следовательно, N=1996.

2)                 По условию задачи число N имеет ровно 6 натуральных делителей. Значит, N состоит из одного простого числа в степени 5, т. е. . Взяв во внимание 6 спецзадачу, запишем сумму делителей числа N:

. Сейчас необходимо решить уравнение в простых числах. Учитывая, что , достаточно перебрать p=2, 3, 5, но ни одно из них не удовлетворяет предъявленным требованиям.

Ответ: N=1996.

Задача 2. Назовем натуральное число палиндромом, если в его десятичной записи все цифры расположены симметрично [1]. Например, числа 21 и 953359 являются палиндромами, а числа 10 и 953953 не являются палиндромами.

1.                Привести пример числа — палиндрома, которое делится на 45.
2.                Сколько существует пятизначных чисел — палиндромов, делящихся на 45?
3.                Найдите десятое по величине число — палиндром, которое делится на 45 [4].

Данная задача относится к иному классу, нежели рассмотренная выше, и для поиска ее решения необходимо опираться на другие знания. В связи с этим дополним блок задач источника [2]:

7.                Делится ли число 1234567890 на 2? 3? 5? 9?

Ответ:_______________.

8.                Какую цифру можно приписать справа к числу 867 так, чтобы полученное число стало кратным 11?

Ответ:_______________.

Примечание: число делится на 11, если разность между суммами цифр, стоящих на четных и на нечетных местах делится на 11 [1].

9.                Запишите наименьшее натуральное число, которое при делении на 4, 9, 11, 25 дает в остатке 1.

Ответ:________________.

Для решения задачи вспомним признак делимости на 4 (25): если число, составленное из последних двух цифр, делится на 4 (25), то и исходное число делится на 4 (25) [1].

10.            Если в составе чисел c единиц, b десятков и а сотен, то пользуются записью вида: 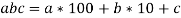, которая называется _______________________.

Рассмотрим решение задачи № 2.

а)                  Например, число 585=13*45.

б)                 Пусть десятичная запись пятизначного числа n имеет вид abcba(специальная задача № 10), где a,b, c — некоторые цифры, a не равно 0. Это число делится на 45 тогда и только тогда, когда оно делится на 5 и на 9 (спецзадача № 7). По признакам делимости на 5 и на 9 получаем, что этому условию удовлетворяют те и только те числа n, для которыхa равно 5 и 2a+2b+c делится на 9. Значит, 2b+c должно давать остаток 8 при делении на 9. Следовательно, 2b+c может равняться 8, 17 и 26.

Если 2b+c=8, то c=8,b=0, или c=6,b=1, или c=4,b=2, или c=2,b=3, или c=0,b=4 — то есть всего 5 вариантов.

Если 2b+c=17, то c=9,b=4, или c=7,b=5, или c=5,b=6, или c=3,b=7, или c=1,b=8 — снова получилось 5 вариантов.

Если 2b+c=26, то c=8,b=9 — всего 1 вариант.

В результате получаем 11 пятизначных чисел — палиндромов, делящихся на 45.

в)                  Заметим, что делящихся на 45 двузначных и однозначных чисел — палиндромов не существует. Если трехзначное число — палиндром имеет десятичную запись aba (специальная задача № 10) и делится на 45 (специальная задача № 7), то a=5 и 2a+b делится на 9. Значит, b при делении на 9 дает в остатке 8. Есть всего один вариант — число 585.

Если четырехзначное число — палиндром имеет десятичную запись abba (специальная задача № 10) и делится на 45 (специальная задача № 7), то a=5 и 2a+b делится на 9. Тогда 5+b делится на 9. Есть всего один вариант — число 5445.

Как доказано в решении пункта б) этой задачи, существует 11 пятизначных чисел — палиндромов с десятичной записью abcba(специальная задача № 10), делящихся на 45. У всех этих чисел a=5. У самого большого из них b=9,c=8 — это тринадцатое по величине число — палиндром, делящееся на 45. Случаям b=8,c=1; b=7,c=3 соответствуют двенадцатое и одиннадцатое по величине числа соответственно. Десятым по величине, делящимся на 45 числом — палиндромом является число 56565.

Ответ: а) 585; б) 11; в) 56565.

В заключение выделим основные понятия, которые пригодятся для построения решения задания № 19 ЕГЭ по математике, и повторим специальные задачи, используемые в этой статье (таблица 1.).

 

Таблица 1

Группа основных понятий и специальных задач, необходимых для решения заданий более высокого уровня единого государственного экзамена.

Понятие	Специальная задача
Простое число	Натуральное число р называется ________________, если имеет только два делителя: 1 и р.
Составное число	Из приведенного ряда зачеркните только составные числа: 1, 2, 4, 8, 11, 17, 22, 15, 20, 34, 41, 43.
Алгоритм установления того, является ли число простым или составным	а) ; б) 2, 3, 5, 7, 11, 13, 17, 19, 23, 29; в) 911=2*455+1; 911=3*303+2; 911=5*182+1; 911=7*130+1; 911=11*82+9; 911=13*70+1; 911=17*53+10; 911=19*47+18; 911=23*39+14; 911=29*31+12; г) 911 — простое число 1.__________________; 2. __________________; 3.__________________; 4. __________________.
Каноническое разложение	Запись числа в виде (*) называется _________________ разложением.
Количество всех натуральных делителей числа	Запомните формулу (*), тогда количество всех натуральных делителей числа р вычисляется по формуле: (**)
Сумма натуральных делителей числа	Если задано каноническое разложение (*) числа n, то сумму его натуральных делителей найдем с помощью формулы: (***)
Десятичная запись	Если в составе чисел c единиц, b десятков и а сотен, то пользуются записью вида: , которая называется _____________________.
Признаки делимости	а) Делится ли число 1234567890 на 2? 3? 5? 9? б) Какую цифру можно приписать справа к числу 867 так, чтобы полученное число стало кратным 11? в) Запишите наименьшее натуральное число, которое при делении на 4, 9, 11, 25 дает в остатке 1. Ответ: а)________; б)_______; в)______.

 

Таким образом, специальные задачи, систематизированные по каждому разделу математики, позволяют быстро и качественно научиться решать задачи ЕГЭ повышенной сложности [2].

 

Литература:

 

1.                Мохина Т. В., Нестерова Л. Ю. Теория чисел. — Арзамас: АГПИ, 2004 — С.34–38
2.                Нестерова Л. Ю. Совокупности специализированных задач для подготовки учащихся к итоговой аттестации по математике / Л. Ю. Нестерова // Задачные конструкции математического развития школьников: сборник статей участников научно-методического семинара / Под общ. ред. С. В. Арюткиной, С. В. Напалкова; Арзамасский филиал ННГУ. — Арзамас, 2015. — 102с. — С.51–53.
3.                Число и сумма натуральных делителей натурального числа / [Электронный ресурс]. — Режим доступа:http://www.diary.ru/~eek/p85182052.htm?oam#more4 (дата обращения: 15. 12. 15)
4.                ЕГЭ. Математика: типовые экзаменационные варианты / Под. ред. И. В. Ященко. — М.: «Национальное образование», 2015. — С.79