Из динамической теории упругости известно [1,2], что поверхность волны Рэлея распространяется в полупространстве с прямолинейными границами. Возникает вопрос, возможно ли распространение волны Рэлея в теле с криволинейными границами? Рассмотрено распространение поверхностных волн в цилиндрическом теле. Уравнение движения упругого тела в цилиндрических координатах (r, ), принимает вид [1]
;(1)
,
с помощью известных преобразований, уравнения (1) могут быть приведенных к виду [2]:
; 
, (2)
где
; 
; 
; 
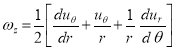
Е и G — модуль упругости и сдвига, — плотность материала, 
— коэффициент Пуассона. Внешние нагрузки на свободной цилиндрической поверхности r = r1 отсутствуют, т. е.
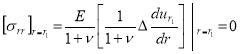, (3)
.
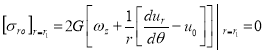Частное решение уравнения (1) ищем в виде:
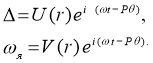(4)
Здесь U и V — есть амплитудная функция, зависящая только от r и
; 
,
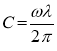— длина волн, С — фазовая скорость распространения волн. Подставляя (4) в (2) переходим к уравнения следующего вида:
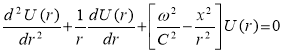. (5)
Решение уравнения (5) в зависимости от постановки задач, выражается через цилиндрические функции
,
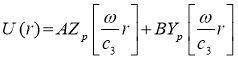где
Jp, Np — функция Бесселя 1-го и 2-го рода р-го порядка, H(1), (2) = Jp INp — функции Ханкеля 1- го и 2-го рода р-го порядка.
В качестве примера рассмотрим распространение волн на границе диска (рис.1 а) и цилиндрической полости (рис. 1 б). В первой задаче в центре диска (r=0) предполагается, что перемещение ограничено. Во второй задаче ставится условие излучения [3] на бесконечность. С помощью этих условий можно найти выражения В, которое равно В=0.
Тогда решение дифференциального уравнения (2) примет вид:
;
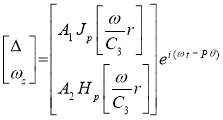Тогда перемещение среды принимает следующий вид:
;
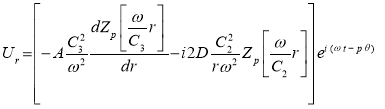
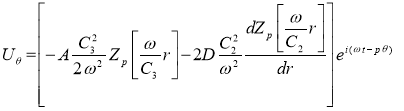Подставляя перемещение в граничные условия, получим алгебраические уравнения второго порядка. Нетривиальное решение (А 0,
D 0) существует только при условии, что определитель матрицы системы уравнений равен нулю, т.е
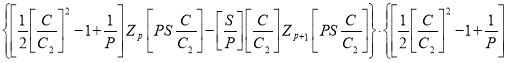
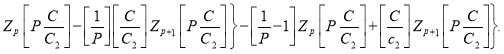(6)
,
.
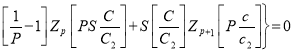Трансцендентные уравнения (6) решаются методом Мюллера. Результаты расчетов представлены на рис.1. Для =0,33 исследованы корни трансцендентного уравнения. Одновременно мы определили четыре корня
(р = 100) С(1) (100) = 0,91194С2; С(2) (100)= 1,0321С2; С(3) (100) =1,051С2;
Из источников [1,2,3] известно, что при Р = 98,С(1) = 0,92С2, а скорость волны Рэлея СR = 0,9194C2.
Результаты расчетов представлены в рисунках 1 и 2. Здесь можно сделать следующие выводы. Когда тело ограничено цилиндрическими границами, также существуют поверхностные волны Рэлея.
В отличие от известных, в этом случае кроме скорости волны Рэлея СR(1) существует счетное множество скоростей (рис. 1).
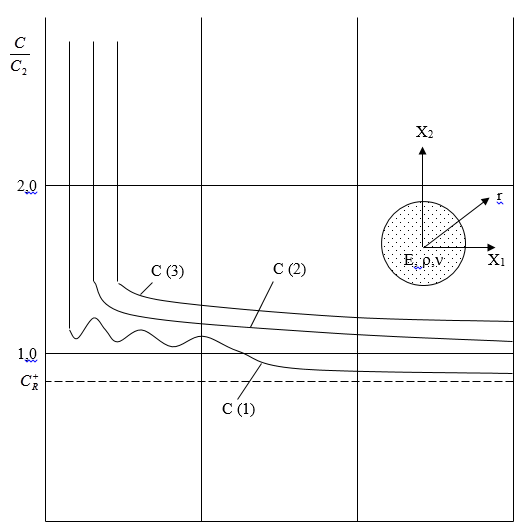
Рис. 1. Зависимости фазовой скорости от длины волн
Литература:
- Гринченко В. Т. Малешко В. В. Гармонические колебания и волны в упругих телах. Киев. Наукова думка. 1981, 263 с.
2. Новацкий В. Теория упругости. М. Мир, 1975, 707 с.
3. Савин Г. Н. Распределение напряжений около отверстий. Киев. Наукова думка, 1968,887 с.
