Ключевые слова: искусственный интеллект, задача удовлетворения ограничений, поиск с возвратом, генетический алгоритм, распространение ограничений, алгоритм Вальца, разметка изображений.
По современным научным данным человеческий мозг содержит огромное число нейронов, он производит и обрабатывает огромное количество логически связанных электрохимических импульсов. Результатами этих процессов являются способность адаптироваться к новым ситуациям, способность к обучению на основе опыта, понимание и применение абстрактных концепций и использование своих знаний для управления окружающей средой.
Ученые пытаются приблизить возможности компьютера к уровню развития человеческого мозга, пытаясь создать интеллектуальные машины и интеллектуальные компьютерные программы. Искусственный интеллект должен думать и действовать рационально, вести и мыслить, как человек.
Одной из важных задач искусственного интеллекта (ИИ) является задача удовлетворения ограничений (УО) (constraint satisfaction problem). Теория УО предлагает удобный аппарат и простую формальную схему для представления и решения комбинаторных задач ИИ. В искусственном интеллекте парадигма УО признана в качестве удобного и эффективного способа моделирования и решения многих прикладных комбинаторных задач. Важная задача оценки конъюнктивных запросов в теории баз данных может рассматриваться как задача УО. Кроме того, задачи УО привлекают большое внимание в теории сложности, так как различные версии задач УО находятся в середине многих стандартных классов сложности.
Задача УО состоит из множества переменных ![]() , множества доменов значений
, множества доменов значений ![]() для каждой переменной
для каждой переменной ![]() , и множества ограничений и отношений. Каждый домен значений является конечным множеством значений, которые может принимать соответствующая переменная. Состояние задачи определяется путем присваивания значений некоторым или всем этим переменным
, и множества ограничений и отношений. Каждый домен значений является конечным множеством значений, которые может принимать соответствующая переменная. Состояние задачи определяется путем присваивания значений некоторым или всем этим переменным ![]() . Присваивание, которое не нарушает никаких ограничений, называется совместимым, или допустимым присваиванием. Полным называется такое присваивание, в котором участвует каждая переменная, а решением задачи CSP является полное присваивание, которое удовлетворяет всем ограничениям.
. Присваивание, которое не нарушает никаких ограничений, называется совместимым, или допустимым присваиванием. Полным называется такое присваивание, в котором участвует каждая переменная, а решением задачи CSP является полное присваивание, которое удовлетворяет всем ограничениям.
Для решения задачи УО применяются различные методы: методы поиска на графах, методы согласования, методы распространения ограничений, генетические методы, итерационные методы и многие другие. В данной статье будут рассмотрены наиболее простые и наиболее широко применяемые методы: метод поиска с возвратом, генетический метод и метод распространения ограничений.
Поиск с возвратом (Backtrackingsearch).
Решение задачи методом поиска с возвратом строится конструктивно последовательным расширением частичного решения. Если на конкретном шаге такое расширение провести не удается, то происходит возврат к более короткому частичному решению, и попытки его расширить продолжаются. Для ускорения перебора с возвратом вычисления всегда стараются организовать так, чтобы была возможность отказаться как можно раньше от как можно большего числа заведомо неподходящих вариантов.
Метод поиска с возвратом является универсальным. Достаточно легко проектировать и программировать алгоритмы решения задач с использованием этого метода. Однако время нахождения решения может быть очень велико даже при небольших размерностях задачи (количестве исходных данных), причём настолько велико, что о практическом применении не может быть и речи.
В качестве примера использования поиска с возвратом возьмем задачу раскраски карты. Формулировка задачи следующая: необходимо раскрасить каждый регион на карте Австралии красным, зеленым или синий цветом таким способом, чтобы ни одна пара соседних регионов не имела одинаковый цвет.
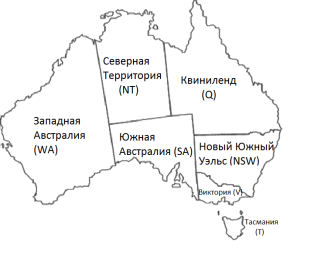
Рис. 1. Задача раскраски карты Австралии
Чтобы сформулировать это задание в виде задачи УО, определим в качестве переменных сокращенные обозначения этих регионов: WA, NT, Q, NSW, V, SA и T. Областью определения каждой переменной является множество цветов {red, green, blue}. Ограничения требуют, чтобы все пары соседних регионов имели разные цвета, например, допустимыми комбинациями для WA и NT являются следующие пары: {{red, green), {red, blue), {green, red), {green, blue), {blue, red), {blue, green)}
Сначала раскрасим первую область любым цветом, а затем пытаемся раскрасить следующие области так, чтобы соседние регионы не были одинаковых цветов. Если на очередном шаге оказалось, что ограничение не выполняется, возвращаемся на шаг назад и меняем цвет ранее раскрашенной области.
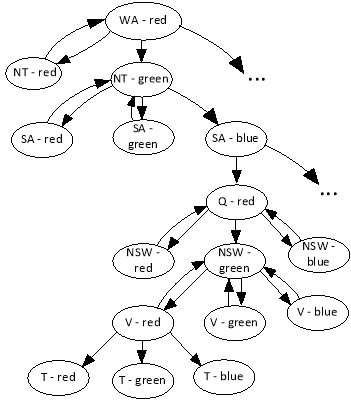
Рис. 2. Граф решения задачи раскраски карты методом поиска с возвратом
Количество возможных решений достаточно велико; например, одним из таких решений является следующее: {WA=red, NT= green, SA=blue, Q=red, NSW=green, V=red, T=red}.
Генетический метод.
Генетический метод основан на принципах селекции: отбор, скрещивание и мутация. При решении задач проводится аналогия с животным миром. Переменные считаем отдельными особями, а их значения, удовлетворяющие ограничения, полезными генами, которые необходимо передать потомству для получения наилучших особей, т. е. решения поставленной задачи.
В начале решения переменным присваиваются случайные значения. Для того, чтобы узнать, «на сколько особи приспособлены», случайно сгенерированное решение проверяется на удовлетворение ограничения. Следующим шагом «скрещиваем лучших особей» и формируем новое «поколение», заменяя худшие решения. Новый набор решений заново оценивается и формируются следующие «поколения». Важно отметить, что на определенном этапе решение может зациклиться, для исключения зацикливания генетический алгоритм предусматривает «мутации». Мутации подразумевают перенимание переменными-потомками свойств переменных-предков с небольшими изменениями.
Рассмотрим применение генетического алгоритма в рамках УО на примере задачи о расстановке N ферзей.
Задача о расстановке N ферзей заключается в том, чтобы расставить на шахматной доске размером N на N клеток фигуры N ферзей так, чтобы они не били друг друга.
Представим в форме ЗУО: переменными являются положения ферзей ![]() ; областью определения каждой переменной — её координаты на доске; ограничением выступает особенность хода фигуры (королева может ходить по вертикали, горизонтали и по диагонали на любое расстояние):
; областью определения каждой переменной — её координаты на доске; ограничением выступает особенность хода фигуры (королева может ходить по вертикали, горизонтали и по диагонали на любое расстояние): ![]() .
.
Попробуем применить генетический метод на доске 8х8.
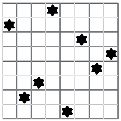
Рис. 3. Задача расстановки N ферзей
В начальный момент времени фигуры расположены в случайном порядке. Проверим, сколько угроз имеет каждая фигура и в следующем «поколении» заменим значения координат фигуры с наибольшим количеством угроз на новые. В нашем случае наибольшее количество угроз приходится на фигуры в третьей и шестой строках, а наименьшее на фигуры во второй и пятой строках. Следующее поколение должно содержать повторяющиеся у родителей наилучшие значения.
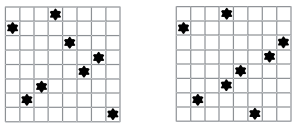
Рис. 4. Задача расстановки N ферзей после 1 и 2х итераций
Продолжая выполнять итерацию за итерацией мы получим следующее решение (одно из 92).
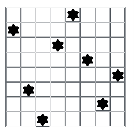
Рис. 5. Решение задачи расстановки N ферзей
Генетический алгоритм, конечно, не может решить задачу, если потребуется найти все её решения, но зато он существенно увеличивает скорость нахождения решения в сравнении с методами перебора или поиска с возвратом.
Распространение ограничений.
Данный метод находит решение задачи, сужая пространство возможных решений исключением избыточных значений из доменов переменных за счет распространения ограничений.
Исследования по распространению ограничений и алгоритмам совместности были инициированы в работе Вольца, в которой был предложен алгоритм распространения ограничений для задач полиэдральной линейной разметки для систем компьютерного видения. Он показал, что для некоторых многогранных фигур достаточно применить основные алгоритмы распространения для решения этих задач.
Алгоритм помогает решить задачу разметки изображений. Цель задачи состоит в распознавании объектов 3-мерного изображения с помощью интерпретации линий на 2-мерных рисунках. Каждое пересечение является переменной. Соседние пересечения накладывают ограничения друг на друга.
Суть метода: разметить все линии и узлы на рисунке с целью упростить процесс идентификации объекта.
Алгоритм решения задачи:
- Обозначаем линии на границе рисунка
- Нумеруем вершины
- Исследуем каждую вершину в порядке нумерации
Применяются 4 вида обозначений линий: «![]() », «
», «![]() », «+» и «-». Стрелками обозначаются линии на границе рисунка. Плюс определяет выпуклость, а минус вогнутость.
», «+» и «-». Стрелками обозначаются линии на границе рисунка. Плюс определяет выпуклость, а минус вогнутость.
Для удобства определения типа фигуры вершины (узлы) фигуры разделяют на 4 типа: L-тип, T-тип, тип Вилка и тип Стрелка.
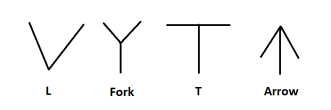
Рис. 6. Типы вершин
В процессе разметки изображения необходимо придерживаться нескольких правил:
- Стрелки должны быть направлены так, чтобы отметить границы рисунка путем обхода в направлении часовой стрелки;
- Непрерывные линии должны иметь одинаковые метки на обоих концах;
- Если вершина типа Вилка не включает границы, то все три линии должны иметь одинаковую метку, т. е. либо все помечены «-», либо «+»;
- У вершин типа Стрелка, имеющих на внешних линиях «стрелки» метки границ, ось «стрелки» должна помечаться меткой «+».
Следуя правилам, можно получиться некоторые шаблоны для всех типов вершин, которыми будем пользоваться в процессе решения задач. То есть все возможные варианты разметки при узлах.

Рис. 7. Варианты разметки
Разберем порядок удовлетворения ограничений на примере конкретной задачи:
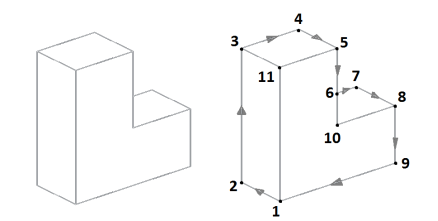
Рис. 7. Пример применения алгоритма Вольца
Сначала обозначим стрелками границы рисунка и пронумеруем узлы. Теперь необходимо обозначить линии внутри рисунка. Для этого проанализируем вершины по порядку. Первая вершина типа Стрелка имеет уже обозначенные два ребра, что накладывает ограничения на выбор метки для третьего ребра. Посмотрев в шаблоны, увидим, что единственной возможной меткой для оставшегося ребра будет «+».
Вторая вершина типа L уже имеет все необходимые метки.
Третья вершина типа Стрелка аналогична вершине первой. Повторяя прошлые шаги, над ребром 3–11 ставим «+».
Дальше необходимо пройтись по всем вершинам. Результатом будет являться полностью размеченная фигура.
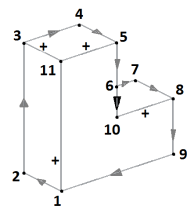
Рис. 8. Решение задачи разметки изображения
Литература:
1. О. А. Щербина Удовлетворение ограничений и программирование в ограничениях
2. Журнал «Интеллектуальные системы» Том 15
3. Лекции Патрика Уинстона (МИТ)







